🧠 신경망이란?

• 딥러닝은 1950년대부터 연구된 인공 신경망(ANN)에서 시작되었다.
• 인공 신경망은 인간의 뇌 구조에서 영감을 받아 만들어진 컴퓨팅 구조이다.

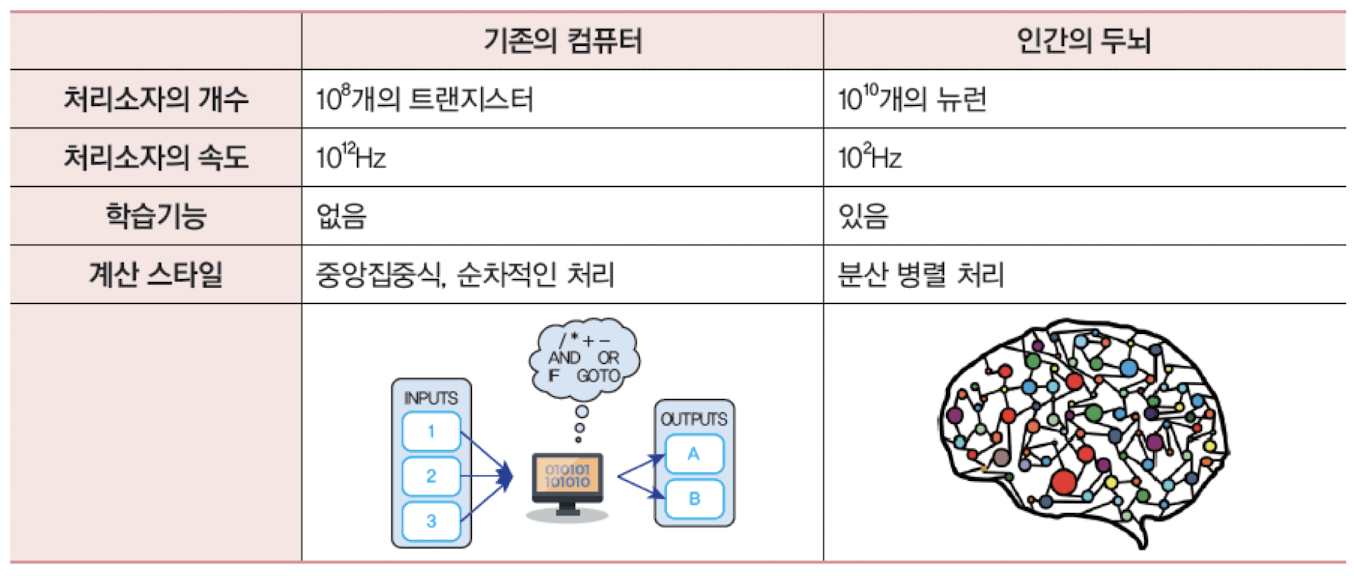
전통컴퓨터와의 차이점

신경망은 유닛 또는 노드들이 연결되어 동작하며, 입력의 총합을 함수로 처리하여 출력을 전달한다.

신경망의 장점

학습 가능성: 데이터만 있다면 예제를 통해 스스로 학습할 수 있다.
오동작에 강한 구조: 일부 유닛이 고장 나도 전체 성능에 큰 영향을 주지 않는다.

---

퍼셉트론 Perceptron

• 퍼셉트론은 1957년에 '로젠블라트'가 고안한 인공 신경망이다. 이는, 가장 단순한 인공신경망으로 불린다.
• 퍼셉트론은 하나의 유닛만 사용하는 모델로 어러개의 입력을 받아서 하나의 신호를 출력하는 장치이다.
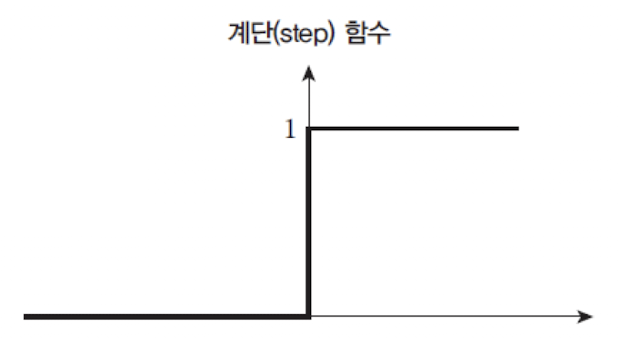
• 뉴런에서는 입력 신호의 가중치 합이 어떤 임계값을 넘어가는 경우에만 활성화되며 1을 출력하고, 그렇지 않으면 0을 출력한다.

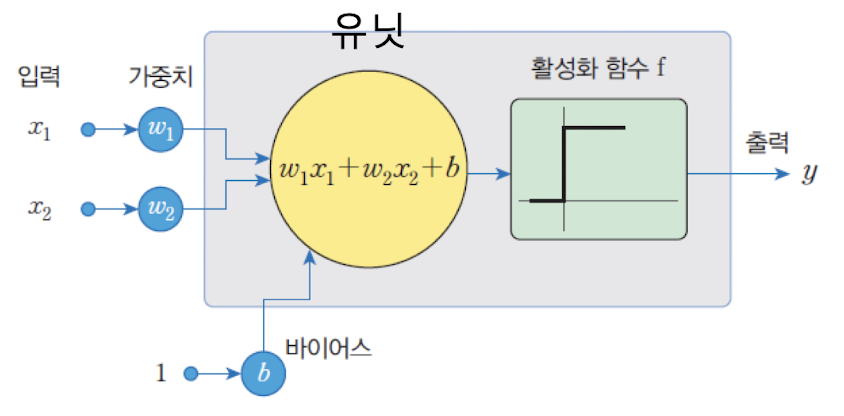
입력이 2이고 출력이 1개인 퍼셉트론 || 가중치(weight) w1, w2 || 바이어스(bias) b

🧮 퍼셉트론의 논리 연산

✔️ AND 연산

x1	x2	y
0	0	0
1	0	0
0	1	0
1	1	1

✔️ OR 연산

x1	x2	y
0	0	0
1	0	1
0	1	1
1	1	1

• $z = w_1 x_1 + w_2 x_2 + b$
• 활성화 함수: $f(z) = \begin{cases} 1 & \text{if } z \ge 0 \\ 0 & \text{if } z < 0 \end{cases}$

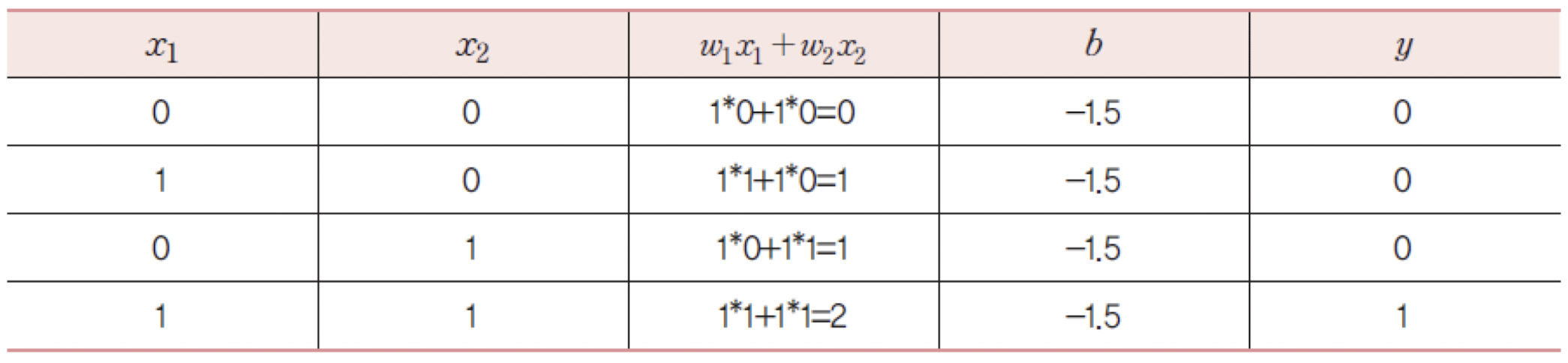
해당 퍼셉트론은 AND 연산에 대한 문제가 없음

---

퍼셉트론 구현 코드

# 순수 파이썬으로 구현한 퍼셉트론
epsilon = 1e-7

def perceptron(x1, x2):
    w1, w2, b = 1.0, 1.0, -1.5
    sum = x1 * w1 + x2 * w2 + b
    if sum > epsilon:
        return 1
    else:
        return 0

print(perceptron(0, 0))  # 출력: 0
print(perceptron(1, 0))  # 출력: 0
print(perceptron(0, 1))  # 출력: 0
print(perceptron(1, 1))  # 출력: 1

출력:
0
0
0
1

# Numpy를 사용한 퍼셉트론 구현
import numpy as np

epsilon = 1e-7

def perceptron(x1, x2):
    X = np.array([x1, x2])
    W = np.array([1.0, 1.0])
    B = -1.5
    sum = np.dot(W, X) + B
    if sum > epsilon:
        return 1
    else:
        return 0

print(perceptron(0, 0))  # 출력: 0
print(perceptron(1, 0))  # 출력: 0
print(perceptron(0, 1))  # 출력: 0
print(perceptron(1, 1))  # 출력: 1

출력:
0
0
0
1

---

퍼셉트론 학습 알고리즘

• 퍼셉트론도 학습을 한다
  신경망이 학습한다고 말하려면, 가중치를 사람이 일일이 설정하지 않아도 스스로 조정하는 알고리즘이 필요하다.
  퍼셉트론에는 이러한 학습 알고리즘이 존재하며, 이를 통해 주어진 데이터로부터 가중치를 조정할 수 있다.

• 훈련 데이터의 구성
  퍼셉트론은 다음과 같은 형태의 훈련 데이터를 사용한다:

  $(𝑥₁, d₁), (𝑥₂, d₂), ..., (𝑥ₘ, dₘ)$

  여기서,
  $x_k$: 입력 벡터 (feature vector)
  $d_k$: 해당 입력에 대한 정답 (target label)
  $m$: 전체 훈련 샘플 수

• 퍼셉트론 출력 식

  $y_k^{(t)} = f(w^{(t)} \cdot x_k + b)$

  에서 바이어스($b$)를 가중치 $w_0$(input을 하나 넣는 식으로)로 간주

  $y_k^{(t)} = f(w^{(t)} \cdot x_k)$

  여기서,
  $x^{(t)}$: 현재 시점 $t$에서의 가중치 벡터
  $x_k$: 입력 벡터
  $f(⋅)$: 활성화 함수 (예: 계단 함수)

---

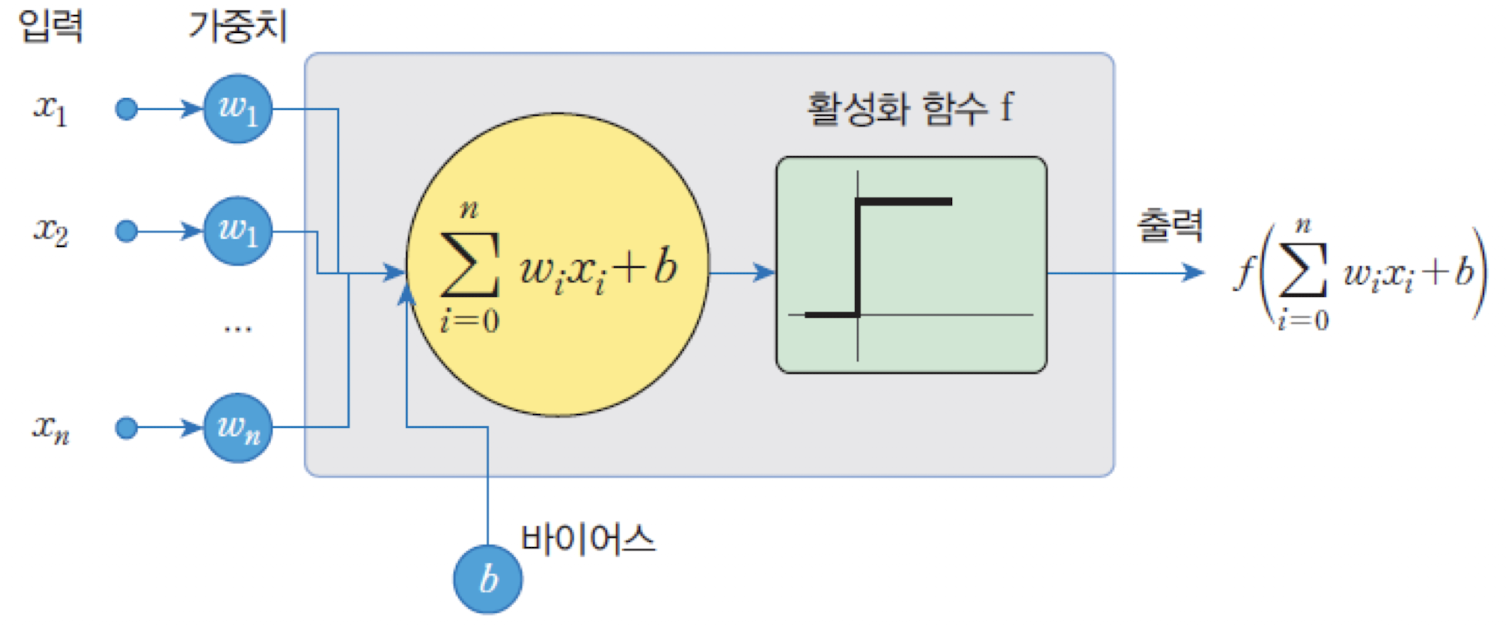
✅ 알고리즘 학습 절차

Input 학습 데이터: $(𝑥₁, d₁), (𝑥₂, d₂), ..., (𝑥ₘ, dₘ)$

• $𝑥_k$는 입력 벡터, $d_k$는 해당 입력의 정답이다.

✔️ 학습 알고리즘 단계

1. 가중치 초기화
   모든 가중치 $w_i$와 바이어스 $b$를 0 또는 작은 난수로 초기화한다.

2. 학습 반복
   가중치가 더 이상 변경되지 않을 때까지 다음 과정을 반복한다:

3. 각 샘플에 대해 다음을 수행

   • 출력 계산:
     $y_k^{(t)} = f(w^{(t)} \cdot x_k)$

   • 가중치 계산:
     $w_i^{(t+1)} = w_i^{(t)} + \eta \cdot (d_k - y_k^{(t)}) \cdot x_{k,i}$

     • $x_{k,i}$는 $k$ 번째 입력 벡터의 $i$번째 요소
     • $d_k$는 정답, $y^{(t)}_k$는 현재 출력값

• 학습률 $η$ (learning rate)
  $0<η≤1$ 범위의 값이며, 가중치가 얼마나 빠르게 변화할지를 결정하는 하이퍼파라미터이다.

• 손실함수 $w_i$에 대한 일차 미분 값이$-2 (d_k - y_k^{(t)}) \cdot x_{k,i}$ 이므로 위와 같은 알고리즘이 가능하다.

---

✔️ 출력 오차에 따른 가중치 변화

정답은 1인데 출력이 0인 경우 (False Negative):

→ 가중치가 증가 → 출력이 더 커질 가능성 증가 → 다음에는 1로 분류할 가능성 ↑

정답은 0인데 출력이 1인 경우 (False Positive):

→ 가중치가 감소 → 출력이 작아질 가능성 증가 → 다음에는 0으로 분류할 가능성 ↑

---

퍼셉트론 학습 알고리즘 코드

# 퍼셉트론 학습 알고리즘 구현

def perceptron_fit(X, Y, epochs=10):
    global W
    eta = 0.2  # 학습률

    for t in range(epochs):
        print("epoch =", t, "======================")
        for i in range(len(X)):
            predict = step_func(np.dot(X[i], W))
            error = Y[i] - predict  # 오차 계산
            W += eta * error * X[i]  # 가중치 업데이트
            print("현재 처리 입력 =", X[i], 
                  "정답 =", Y[i], 
                  "출력 =", predict, 
                  "변경된 가중치 =", W)
        print("================================")

# 퍼셉트론 예측 함수
def perceptron_predict(X, Y):
    global W
    for x in X:
        print(x[0], x[1], "->", step_func(np.dot(x, W)))

# 학습 및 예측 실행
perceptron_fit(X, y, 6)
perceptron_predict(X, y)

epoch= 0 ======================
현재 처리 입력= [0 0 1] 정답= 0 출력= 0 변경된 가중치= [0. 0. 0.]
현재 처리 입력= [0 1 1] 정답= 0 출력= 0 변경된 가중치= [0. 0. 0.]
현재 처리 입력= [1 0 1] 정답= 0 출력= 0 변경된 가중치= [0. 0. 0.]
현재 처리 입력= [1 1 1] 정답= 1 출력= 0 변경된 가중치= [0.2 0.2 0.2]
================================
epoch= 1 ======================
현재 처리 입력= [0 0 1] 정답= 0 출력= 1 변경된 가중치= [0.2 0.2 0. ]
현재 처리 입력= [0 1 1] 정답= 0 출력= 1 변경된 가중치= [ 0.2 0. -0.2]
현재 처리 입력= [1 0 1] 정답= 0 출력= 0 변경된 가중치= [ 0.2 0. -0.2]
현재 처리 입력= [1 1 1] 정답= 1 출력= 0 변경된 가중치= [0.4 0.2 0. ]
================================
epoch= 2 ======================
현재 처리 입력= [0 0 1] 정답= 0 출력= 0 변경된 가중치= [0.4 0.2 0. ]
현재 처리 입력= [0 1 1] 정답= 0 출력= 1 변경된 가중치= [ 0.4 0. -0.2]
현재 처리 입력= [1 0 1] 정답= 0 출력= 1 변경된 가중치= [ 0.2 0. -0.4]
현재 처리 입력= [1 1 1] 정답= 1 출력= 0 변경된 가중치= [ 0.4 0.2 -0.2]
================================
epoch= 3 ======================
현재 처리 입력= [0 0 1] 정답= 0 출력= 0 변경된 가중치= [ 0.4 0.2 -0.2]
현재 처리 입력= [0 1 1] 정답= 0 출력= 0 변경된 가중치= [ 0.4 0.2 -0.2]
현재 처리 입력= [1 0 1] 정답= 0 출력= 1 변경된 가중치= [ 0.2 0.2 -0.4]
현재 처리 입력= [1 1 1] 정답= 1 출력= 0 변경된 가중치= [ 0.4 0.4 -0.2]
================================
epoch= 4 ======================
현재 처리 입력= [0 0 1] 정답= 0 출력= 0 변경된 가중치= [ 0.4 0.4 -0.2]
현재 처리 입력= [0 1 1] 정답= 0 출력= 1 변경된 가중치= [ 0.4 0.2 -0.4]
현재 처리 입력= [1 0 1] 정답= 0 출력= 0 변경된 가중치= [ 0.4 0.2 -0.4]
현재 처리 입력= [1 1 1] 정답= 1 출력= 1 변경된 가중치= [ 0.4 0.2 -0.4]
================================
epoch= 5 ======================
현재 처리 입력= [0 0 1] 정답= 0 출력= 0 변경된 가중치= [ 0.4 0.2 -0.4]
현재 처리 입력= [0 1 1] 정답= 0 출력= 0 변경된 가중치= [ 0.4 0.2 -0.4]
현재 처리 입력= [1 0 1] 정답= 0 출력= 0 변경된 가중치= [ 0.4 0.2 -0.4]
현재 처리 입력= [1 1 1] 정답= 1 출력= 1 변경된 가중치= [ 0.4 0.2 -0.4]
================================
0 0 -> 0
0 1 -> 0
1 0 -> 0
1 1 -> 1

sklearn(scikit-learn)기반 퍼셉트론 코드

from sklearn.linear_model import Perceptron

# 샘플과 레이블
X = [[0, 0], [0, 1], [1, 0], [1, 1]]
y = [0, 0, 0, 1]

# 퍼셉트론 모델 생성
# tol은 조기 종료 조건, random_state는 난수 시드
clf = Perceptron(tol=1e-3, random_state=0)

# 학습 수행
clf.fit(X, y)

# 예측 수행
print(clf.predict(X))  # 출력: [0 0 0 1] (예상)

[0 0 0 1]

---

퍼셉트론의 한계점

• XOR 연산

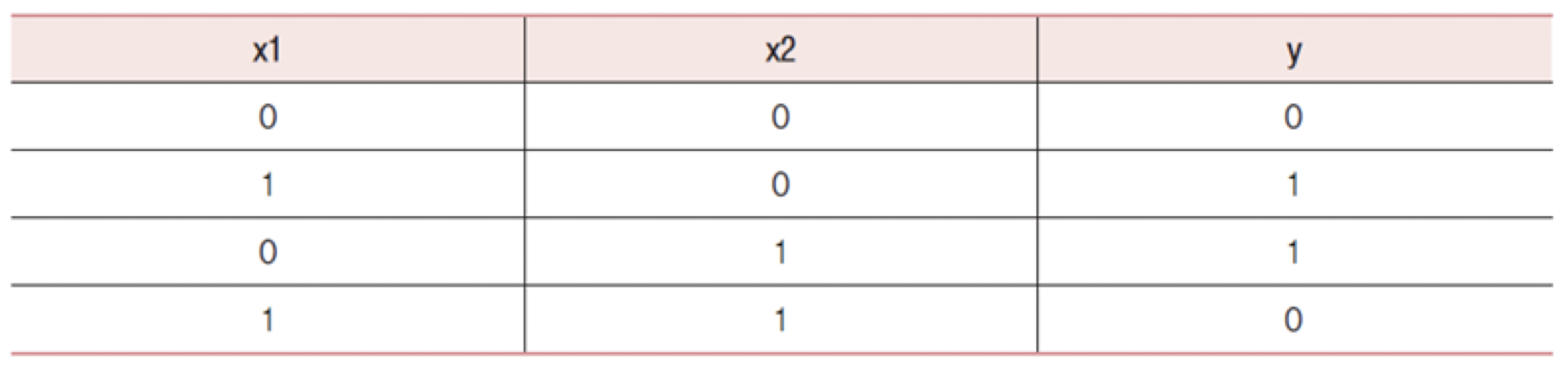
아래와 같이 원하는 출력이 나오지 않는다.

……………
X = np.array([ # 훈련 데이터 세트
[0, 0, 1], # 맨 끝의 1은 바이어스를 위한 입력 신호 1이다.
[0, 1, 1], # 맨 끝의 1은 바이어스를 위한 입력 신호 1이다.
[1, 0, 1], # 맨 끝의 1은 바이어스를 위한 입력 신호 1이다.
[1, 1, 1] # 맨 끝의 1은 바이어스를 위한 입력 신호 1이다.
])
y = np.array([0, 1, 1, 0]) # 정답을 저장하는 넘파이 행렬 (XOR)
……………

...
0 0 -> 1
0 1 -> 1
1 0 -> 0
1 1 -> 0

---

✅ 선형 분류 가능 문제

• 퍼셉트론은 선형 분류자이다
  퍼셉트론은 입력 패턴을 직선(linear decision boundary)을 기준으로 분류하는 선형 분류자(linear classifier)이다.

• 퍼셉트론의 결정 경계
  퍼셉트론에서 가중치와 바이어스는 2차원 입력 공간에서 다음과 같은 직선으로 해석된다: 그 후 영역에 따라 출력을 0과 1로 분류된다.

  $w_1 x_1 + w_2 x_2 + b = 0$

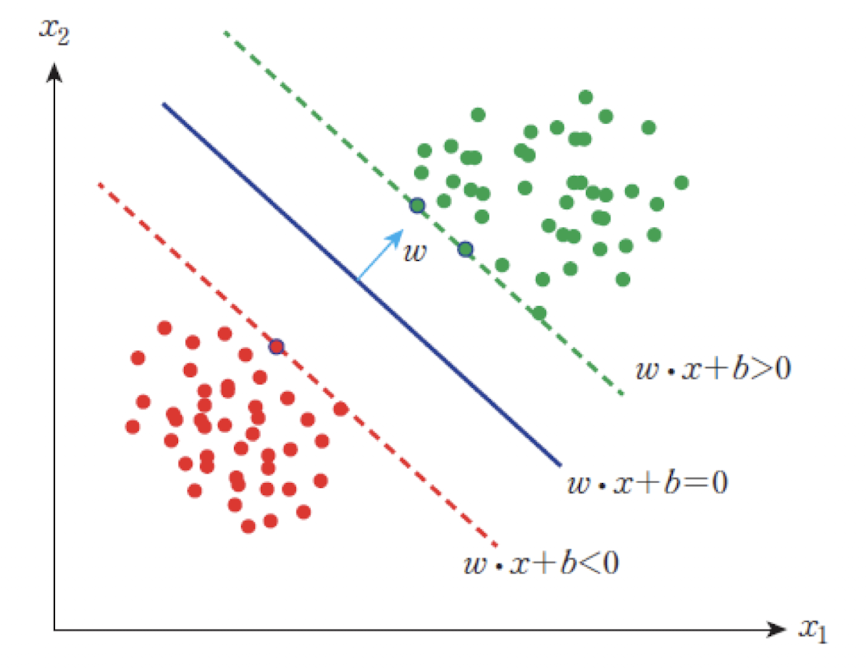
한 개의 직선으로 0과 1을 명확하게 나눌 수 있는 문제를 선형 분리 가능 문제(linear separable problem)라고 한다.

• AND나 OR연산은 선형 분류 가능 문제이나, XOR은 그렇지 않다.

---

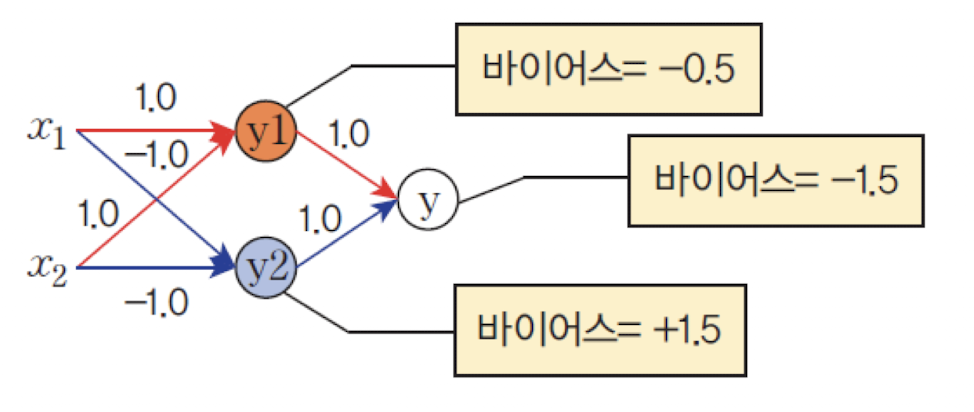
✅ 다층 퍼셉트론을 통한 XOR문제 해결

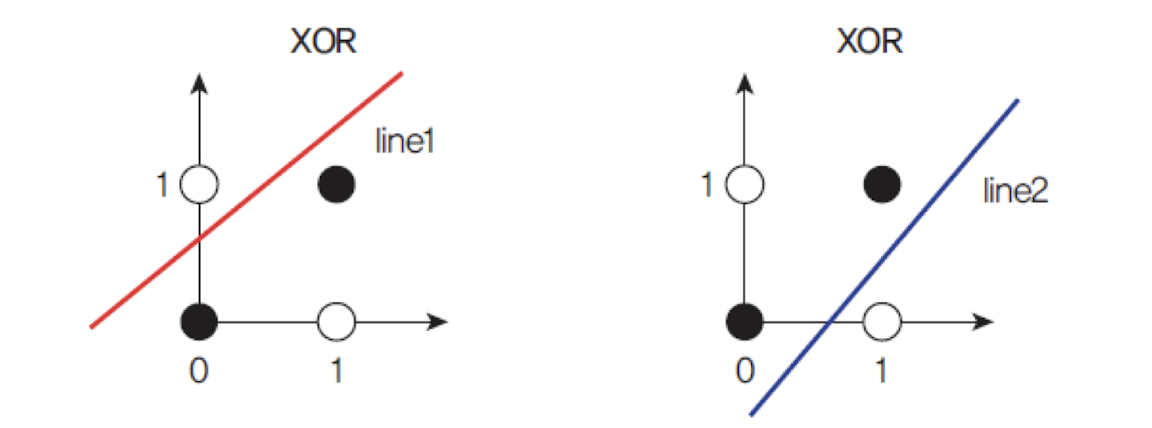
• XOR 문제는 직선 하나로 해결되지 않는다
  XOR 연산은 단일 직선으로는 올바르게 분류할 수 없는 선형 분리 불가능 문제이다.
  정확하게 분류하려면 최소 2개의 결정 경계(직선)가 필요하다.

• 다층 구조의 필요성
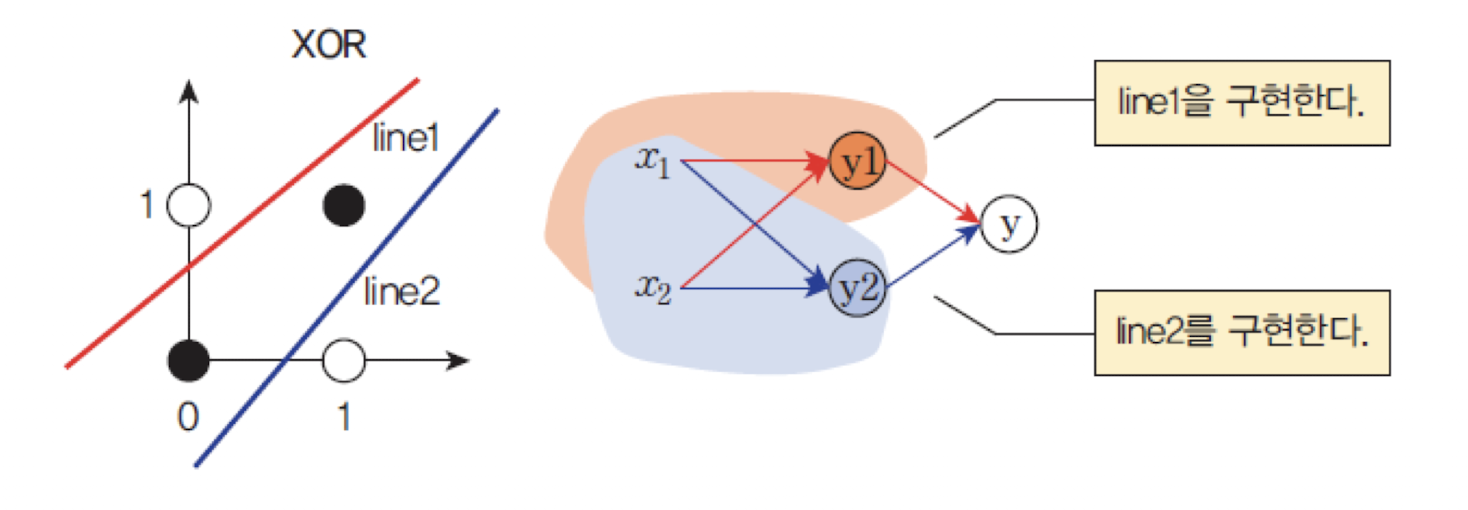
  하나의 유닛(노드)로는 XOR 문제를 분리할 수 없다.
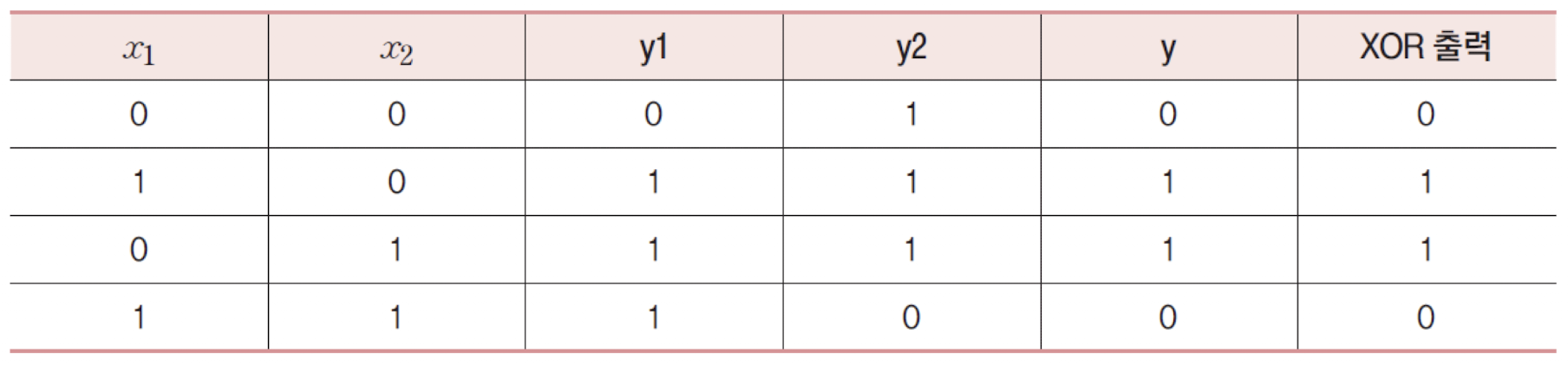
  따라서 다음과 같이 3개의 유닛(y₁, y₂, y)이 필요하다:

  • $y_1$: 첫 번째 직선을 기준으로 분류
  • $y_1$: 두 번째 직선을 기준으로 분류
  • $y$: $y_1, y_2$의 출력을 결합하여 최종 출력

• 은닉층을 추가한 구조: MLP
  퍼셉트론에서 입력층과 출력층 사이에 은닉층(hidden layer)을 추가하면 XOR 문제를 해결할 수 있다.
  이러한 구조를 다층 퍼셉트론(Multilayer Perceptron, MLP)이라고 한다.

---

✅ 다층 퍼셉트론과 역전파 알고리즘

• 다층 퍼셉트론의 층 수 정의
  일반적으로 신경망에서 입력층, 은닉층, 출력층이 존재하지만,
  가중치가 적용되는 층은 은닉층과 출력층뿐이다.
  따라서 신경망이 총 3개의 층으로 구성되어 있어도, 실제로는 2층 퍼셉트론이라고 부르기도 한다.

• 과거의 한계와 예언
  Minsky와 Papert는 1969년 저서에서 다층 퍼셉트론을 학습시키는 것이 매우 어렵다고 주장하였다.
  이 때문에 한동안 퍼셉트론 연구는 정체되었고, AI 겨울이라 불리는 침체기를 맞이하게 된다.

• 역전파 알고리즘의 재발견
  하지만 1980년대 중반, Rumelhart, Hinton 등의 연구자들이
  다층 퍼셉트론을 효율적으로 학습시킬 수 있는 역전파 알고리즘(Backpropagation)을 재발견하였다.
  이로 인해 인공 신경망은 다시 주목을 받게 되었고, 오늘날 딥러닝의 기반이 되었다.