
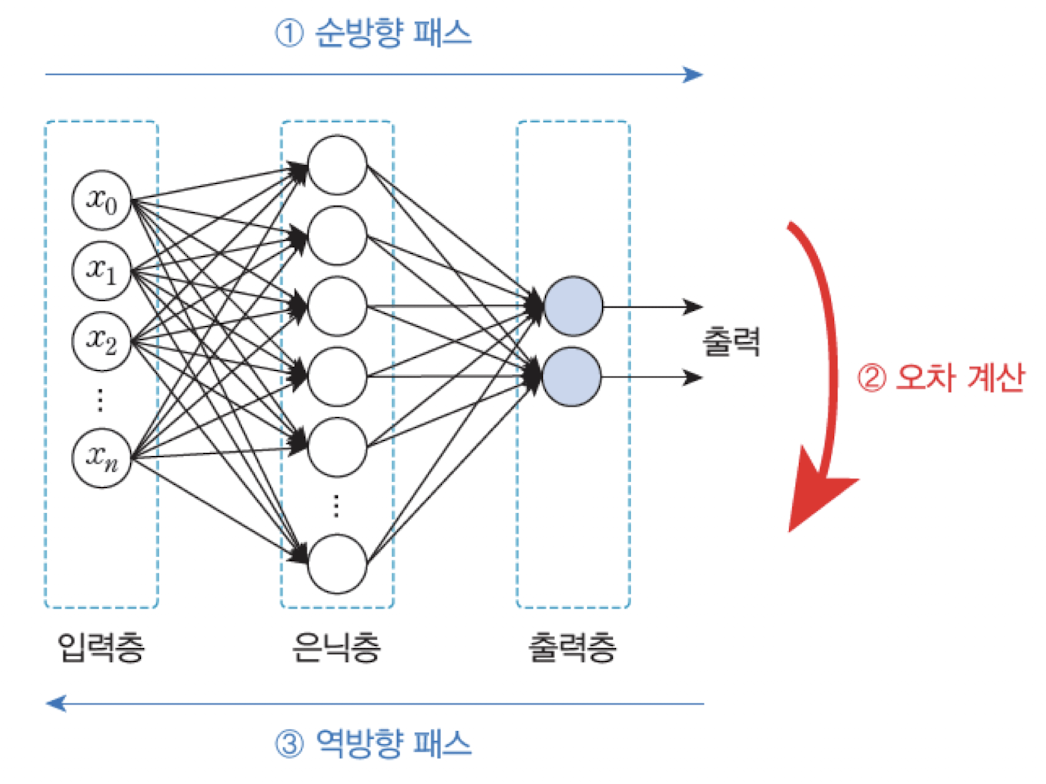
다층 퍼셉트론 (MLP)
다층 퍼셉트론은 입력층(input layer)과 출력층(output layer) 사이에 은닉층(hidden layer)을 포함한 인공신경망 구조이다.
각 층은 뉴런으로 구성되며, 층 간에는 가중치(weight)가 연결되어 있다.
-
순방향 패스(Forward Pass)
입력이 주어지면 이를 신경망의 각 층을 따라 순방향으로 전파시켜 출력을 계산한다. 이 과정을 통해 신경망은 현재의 입력에 대한 예측 값을 생성하게 된다. -
오차 계산(Error Estimation)
신경망의 출력과 정답(label) 간의 차이를 계산하여 오차(error)를 구한다. 이 오차는 학습 과정에서 중요한 정보로 활용된다. -
역방향 패스(Backward Pass)
계산된 오차를 바탕으로, 신경망의 가중치와 바이어스 값을 조정한다. 이는 오차를 줄이기 위한 방향으로 진행되며, 일반적으로 역전파 알고리즘(backpropagation)이 사용된다.
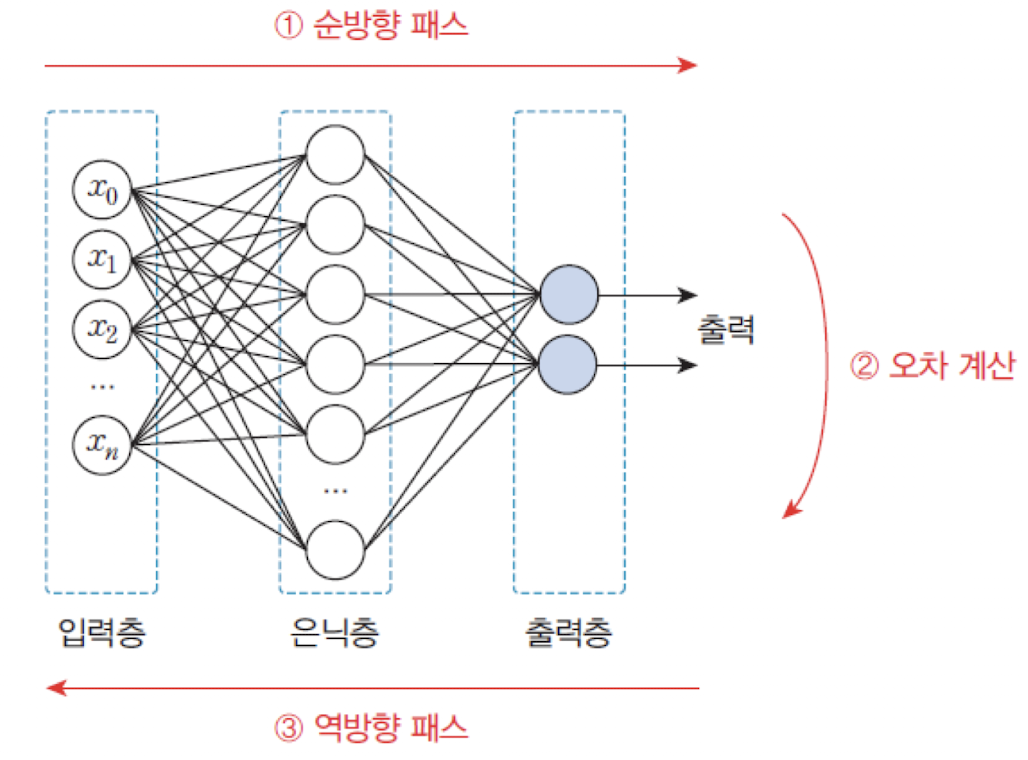
📖 은닉층이 존재하는 MLP를 학습시키는 방법
-
1980년대에
역전파 알고리즘(backpropagation)이 개발되었고, 지금까지도 딥러닝의 근간이 되고 있다. -
역전파 알고리즘(backpropatation) 이란 신경망의 출력과 정답과의 차이, 즉
오차를역방향으로 전파시키면서 오차를 줄이는 방향으로가중치(weight)와바이어스(bias)를 변경하는 알고리즘이다. -
이 과정에서 핵심적인 수학 알고리즘은
경사하강법(gradient descent)이다.
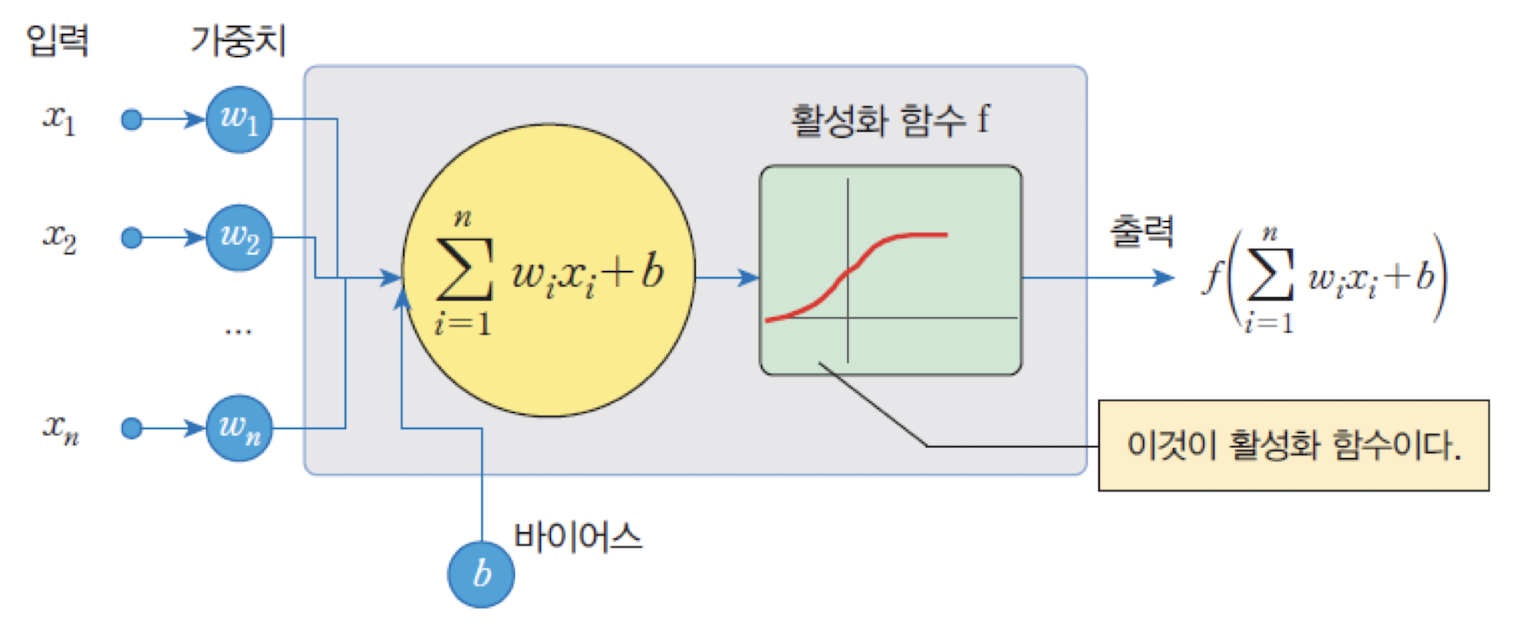
💡 Activation Function (활성화함수)
활성화 함수는 입력의 총합을 받아 출력값을 계산하는 함수이다.
✔️ 퍼셉트론의 계단 함수: 초기 퍼셉트론에서는 계단 함수(step function)를 사용하였다.
✔️ MLP의 비선형 함수: MLP에서는 다양한 비선형 함수(nonlinear function)들이 활성화 함수를 사용하여 복잡한 패턴을 학습할 수 있게 해준다.
-
일반적으로 활성화 함수로는
비선형 함수가 많이 사용된다. -
선형함수 레이어는 여러개를 결합해도 결국은 선형 함수 하나의 레이어로 대치될 수 있다는 것이 수학적으로 증명되었기 때문이다.
(복잡한 함수, 고차원적 패턴, 비선형적 관계들을 모델이 학습할 수 있게 된다.)
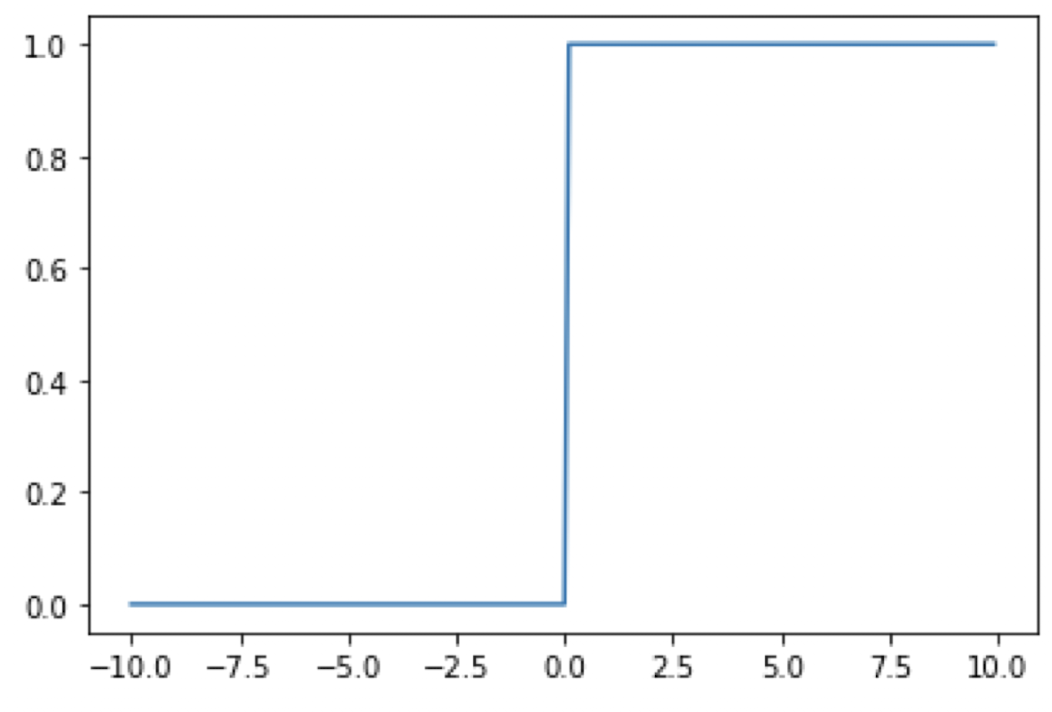
✔️ Step Function (계단 함수)
- 입력 신호의 총합이
0을 넘으면1을 출력하고, 그렇지 않으면0을 출력
📦 Code
# 계단 함수 정의 (방법 1: 조건문 사용)
def step(x):
if x > 0.000001: # 부동 소수점 오차 방지
return 1
else:
return 0
# 계단 함수 정의 (방법 2: 넘파이 배열을 받기 위하여 변경)
def step(x):
result = x > 0.000001 # True 또는 False
return result.astype(np.int32) # 정수로 반환 (1 또는 0)import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-10.0, 10.0, 0.1)
y = step(x)
plt.plot(x, y); plt.show()✔️ Sigmoid Function (시그모이드 함수)
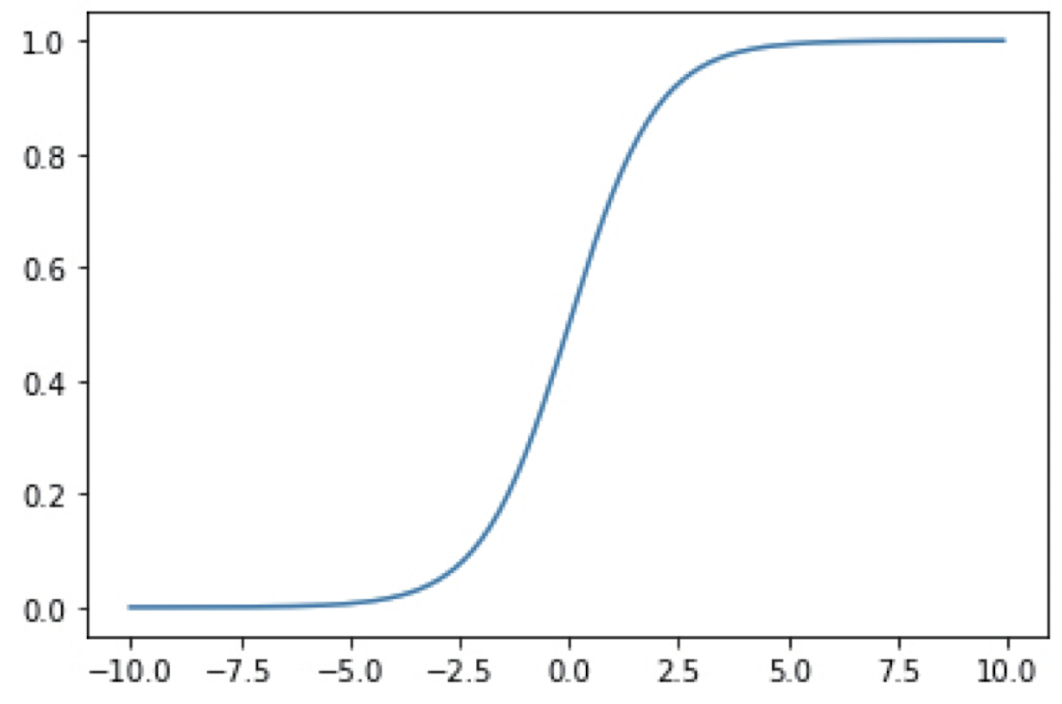
-
S자 형태를 가짐 -
1980년대부터 사용되어 온 전통적인 활성화 함수. 계단함수는 에서 급격하게 변화하여 미분이 불가능하지만 시그모이드 함수는
매끄럽게 변화하기 떄문에 언제 어디서나미분이 가능하다는 장점이 있다. -
경사하강법이라는 최적화 기법을 적용할 수 있다.
📦 Code
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1.0 / (1.0 + np.exp(-x))
x = np.arange(-10.0, 10.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.show()
✔️ ReLU Function (Rectified Linear Unit 함수)
-
최근에 많이 사용되는 활성화 함수.
-
입력이
0을 넘으면그대로출력, 입력이0보다 작으면 출력은0이 된다. -
미분도 간단하고 심층신경망에서 나타나는
gradient 감쇠가 일어나지 않아서 많이 사용된다.
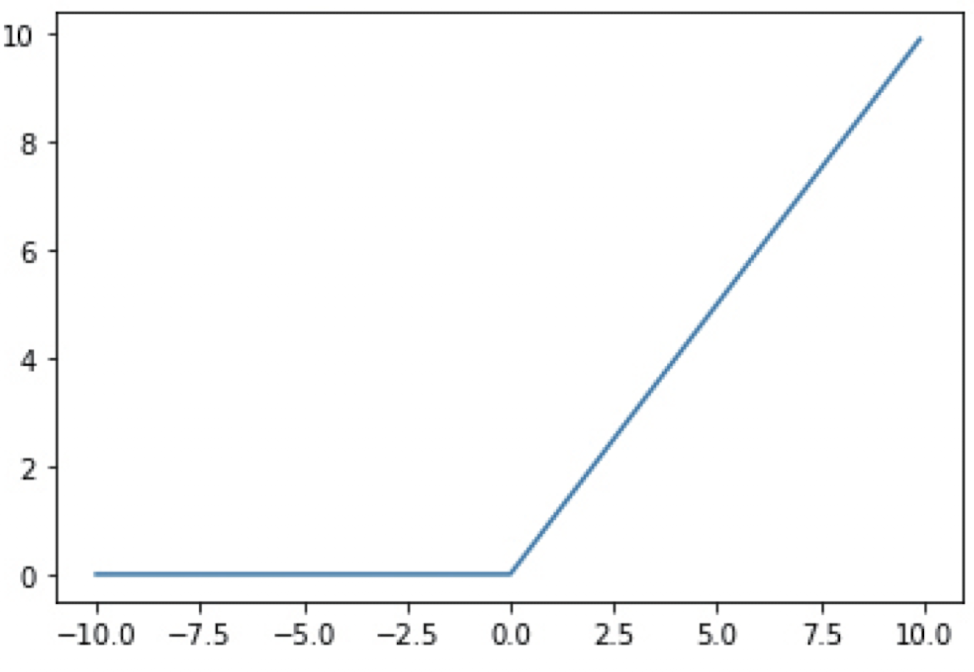
📦 Code
import numpy as np
import matplotlib.pyplot as plt
def relu(x):
return np.maximum(x, 0)
x = np.arange(-10.0, 10.0, 0.1)
y = relu(x)
plt.plot(x, y)
plt.show()✔️ tanh Function (Hyperbolic tangent 함수)
-
numpy에서 제공하고 있기 때문에, 별도의 함수 작성이 필요하지 않다. -
시그모이드 함수와 아주 비슷하지만 출력값이
-1에서1까지 이다. -
RNN에서 많이 사용된다.

📦 Code
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-np.pi, np.pi, 60)
y = np.tanh(x)
plt.plot(x, y)
plt.show()순방향 패스 (Forward Pass)
-
순방향 패스는 입력 신호가입력층에서 시작하여은닉층을 거쳐출력층으로 전파되는 과정을 의미한다. -
은닉층의 첫 번째 유닛에 대한 계산식은 다음과 같다.- : 입력 에서 은닉 유닛 로 가능 가중치
- : 바이어스 항
- : 활성화 함수 (예: sigmoid)
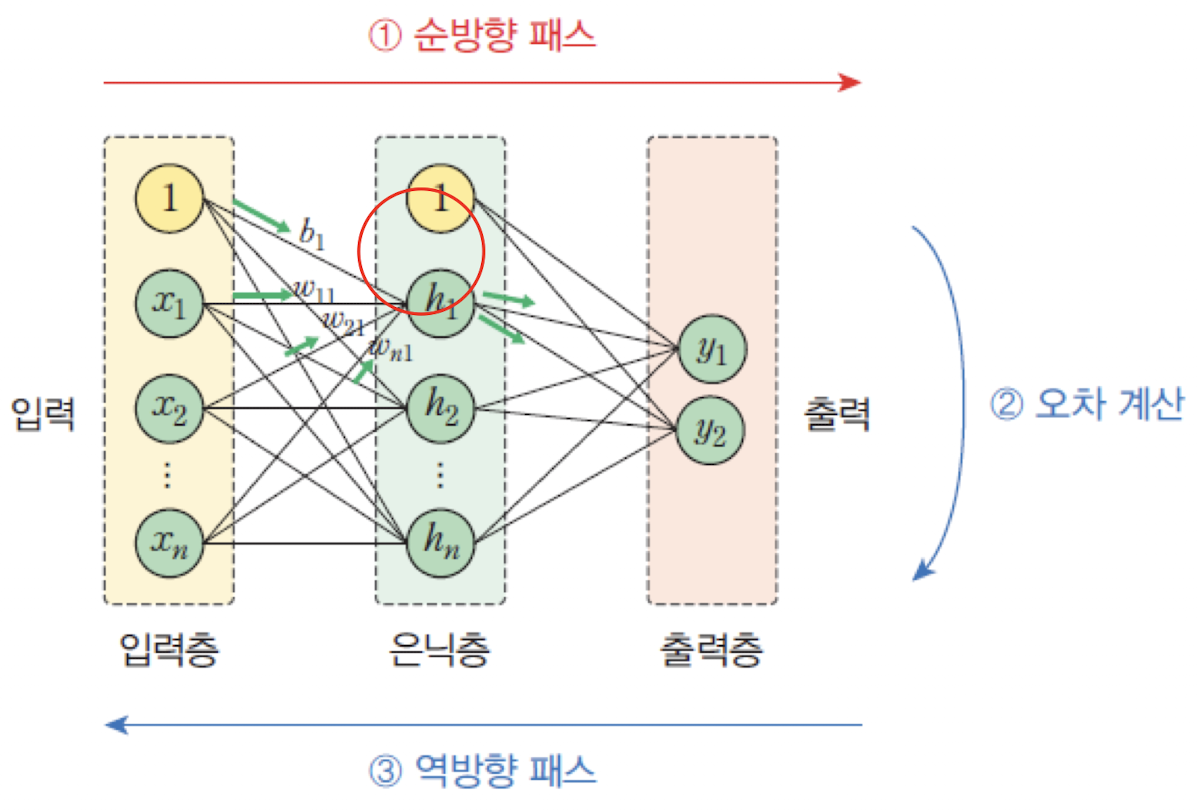
🔗 MLP의 순방향 패스_default
XOR 문제의 첫 번째 훈련 샘플 에 대한 은닉층과 출력층의 계산 흐름
✅ 전체 구조 요약
- 입력층:
- 은닉층: (
시그모이드함수 사용 )- 출력층:
모든 노드는 가중치 와 바이어스 를 통해 연결되어 있음.
📌 은닉 유닛 계산
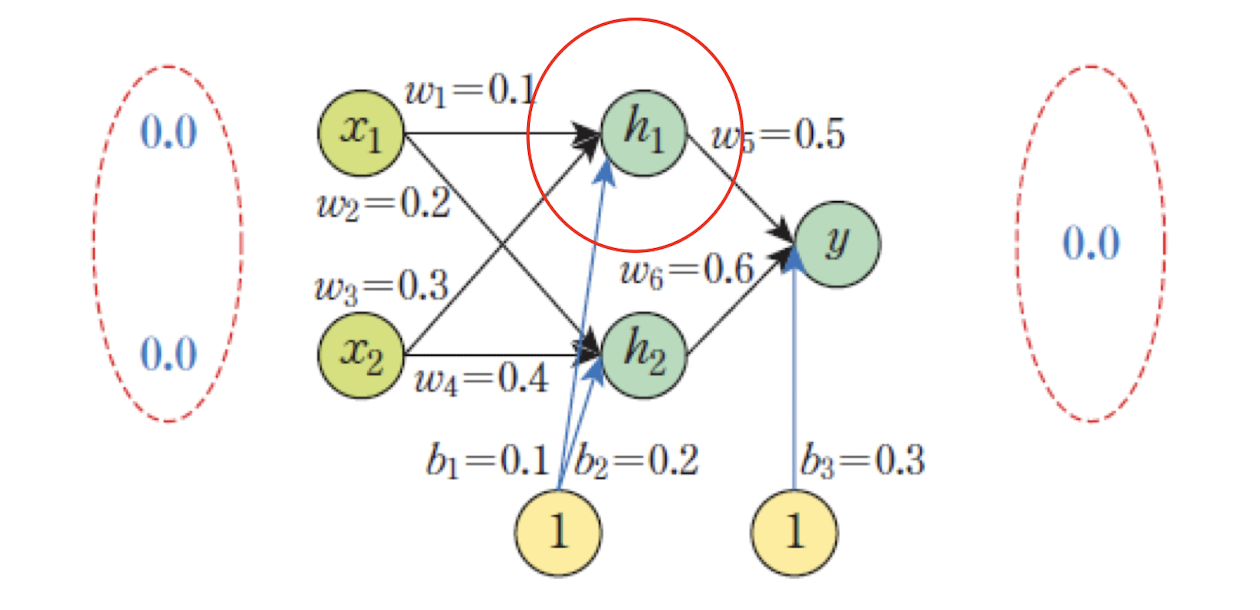
-
활성화 함수(sigmoid) 적용:
-
즉, 의 출력은 약
📌 은닉 유닛 계산
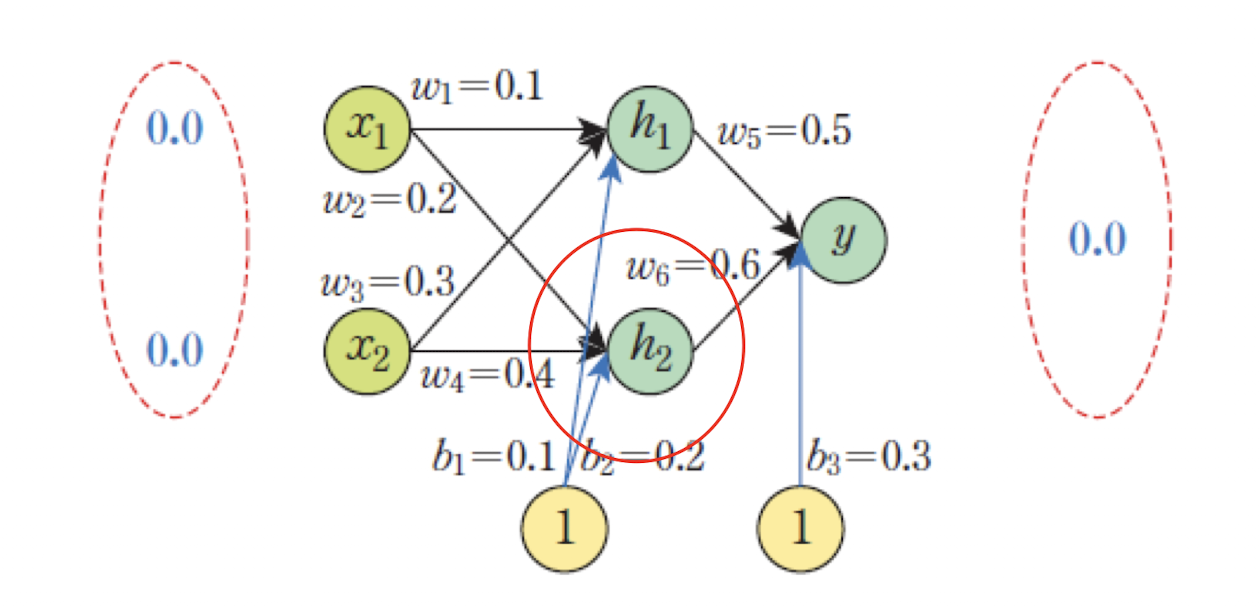
-
선형 결합 값:
-
활성화 함수(
sigmoid) 적용: -
즉, 의 출력은 약
📌 출력층 계산 과정

-
활성화 함수(
sigmoid) 적용: -
즉, 출력값은 약 0.71
📌 오차 확인
-
정답(label)은
0 -
신경망의 출력은
0.709383
➡️ 오차가 상당히 큼 → 역전파를 통해 가중치를 조정해야 함
🔗 MLP의 순방향 패스_행렬기반
📌 입력 → 은닉층 (첫 번째 레이어)
-
스칼라 계산:
-
행렬로 표현:
-
활성화 함수 (
sigmoid) 적용:
📌 은닉층 → 출력층 (두 번째 레이어)
-
스칼라 계산:
-
행렬로 표현:
-
활성화 함수 (
sigmoid) 적용:
➡️ 계산 효율 향상
➡️ 파이썬, 텐서플로우 코드 작성 용이
➡️ 미분(역전파)도 깔끔하게 정리됨
📦 Code
import numpy as np
# 시그모이드 함수
def actf(x):
return 1 / (1 + np.exp(-x))
# 시그모이드 함수의 미분
def actf_deriv(x):
return x * (1 - x)
# 신경망 구조 정의
inputs = 2 # 입력 유닛 개수
hiddens = 2 # 은닉 유닛 개수
outputs = 1 # 출력 유닛 개수
# 학습률 설정
learning_rate = 0.2
# XOR 훈련 데이터 (입력과 정답)
X = np.array([
[0, 0],
[0, 1],
[1, 0],
[1, 1]
])
T = np.array([
[0],
[1],
[1],
[0]
])# 가중치와 바이어스 초기화
W1 = np.array([[0.10, 0.20],
[0.30, 0.40]])
W2 = np.array([[0.50],
[0.60]])
B1 = np.array([0.1, 0.2])
B2 = np.array([0.3])
# 순방향 전파 함수
def predict(x):
layer0 = x # 입력층
Z1 = np.dot(layer0, W1) + B1 # 은닉층 선형 결합
layer1 = actf(Z1) # 은닉층 활성화
Z2 = np.dot(layer1, W2) + B2 # 출력층 선형 결합
layer2 = actf(Z2) # 출력층 활성화 (예측값)
return layer0, layer1, layer2
# 순서대로 계산됨def test():
for x, y in zip(X, T):
x = np.reshape(x, (1, -1)) # 입력을 2차원으로 변환 (1행, n열)
layer0, layer1, layer2 = predict(x)
print(x, y, layer2)
# 테스트 실행
test()
[[0 0]] [1] [[0.70938314]]
[[0 1]] [0] [[0.72844306]]
[[1 0]] [0] [[0.71791234]]
[[1 1]] [1] [[0.73598705]]
# 학습이 없으므로 난수만 출력된다.경사하강법 (Gradient Descent)
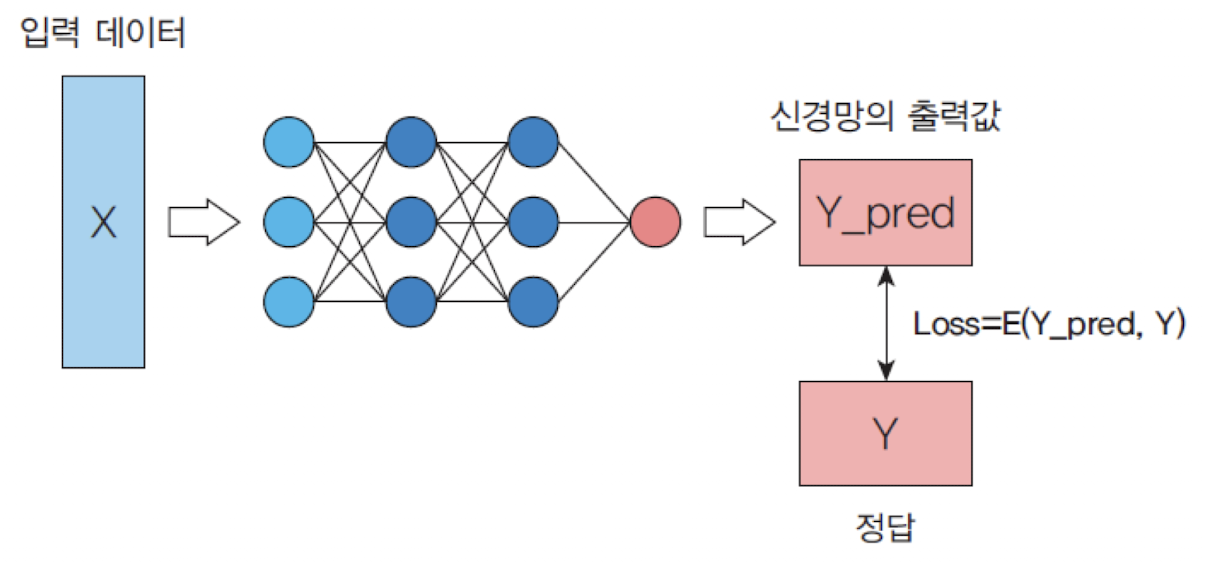
📉 손실 함수 (Loss Function)
-
신경망에서 학습을 시킬 때 는
실제 출력과원하는 출력사이의오차를 이용한다. -
신경망에서도 학습의 성과를 나타내는 지표를
손실함수(loss function)
📌 평균제곱 오차 (MSE)
예측값과 정답 간의 평균 제곱 오차
- : 출력층 유닛 의 예측값
- : 해당 유닛의 정답값
- : 현재 가중치 에 대한 오차 값
⚠️ 앞의 는 미분을 간단하게 만들기 위해 붙는 상수
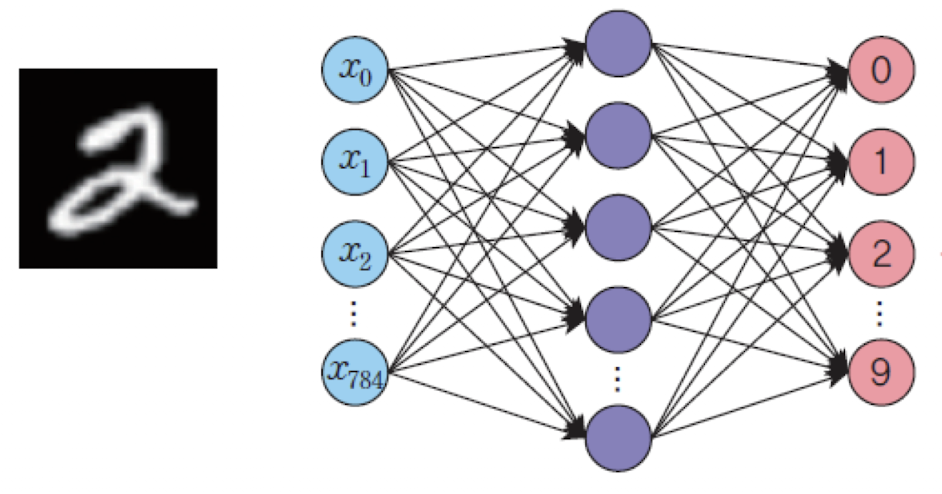
import numpy as np
# 예측값과 정답값
y = np.array([0.0, 0.0, 0.8, 0.1, 0.0, 0.0, 0.0, 0.1, 0.0, 0.0])
target = np.array([0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0])
# 평균 제곱 오차 함수 정의
def MSE(target, y):
return 0.5 * np.sum((y - target) ** 2)
# 정답에 가까운 예측
print(MSE(target, y)) # 0.029999...
# 예측값이 정답과 크게 다른 경우
y = np.array([0.9, 0.0, 0.1, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0])
print(MSE(target, y)) # 0.81
📌 경사하강법 (Gradient Descent)
-
역전파 알고리즘은 신경망 학습 문제를 최적화 문제(optimization)로 접근한다.
-
손실 함수의 기울기(1차 미분값)를 사용하여, 오차를 줄이는 방향으로 가중치를 조정하는 최적화 알고리즘이다.
- : 신경망의 가중치 파라미터
- : 가중치에 따른 손실 함수
- : 손실을 최소화하는 값을 구한다는 의미
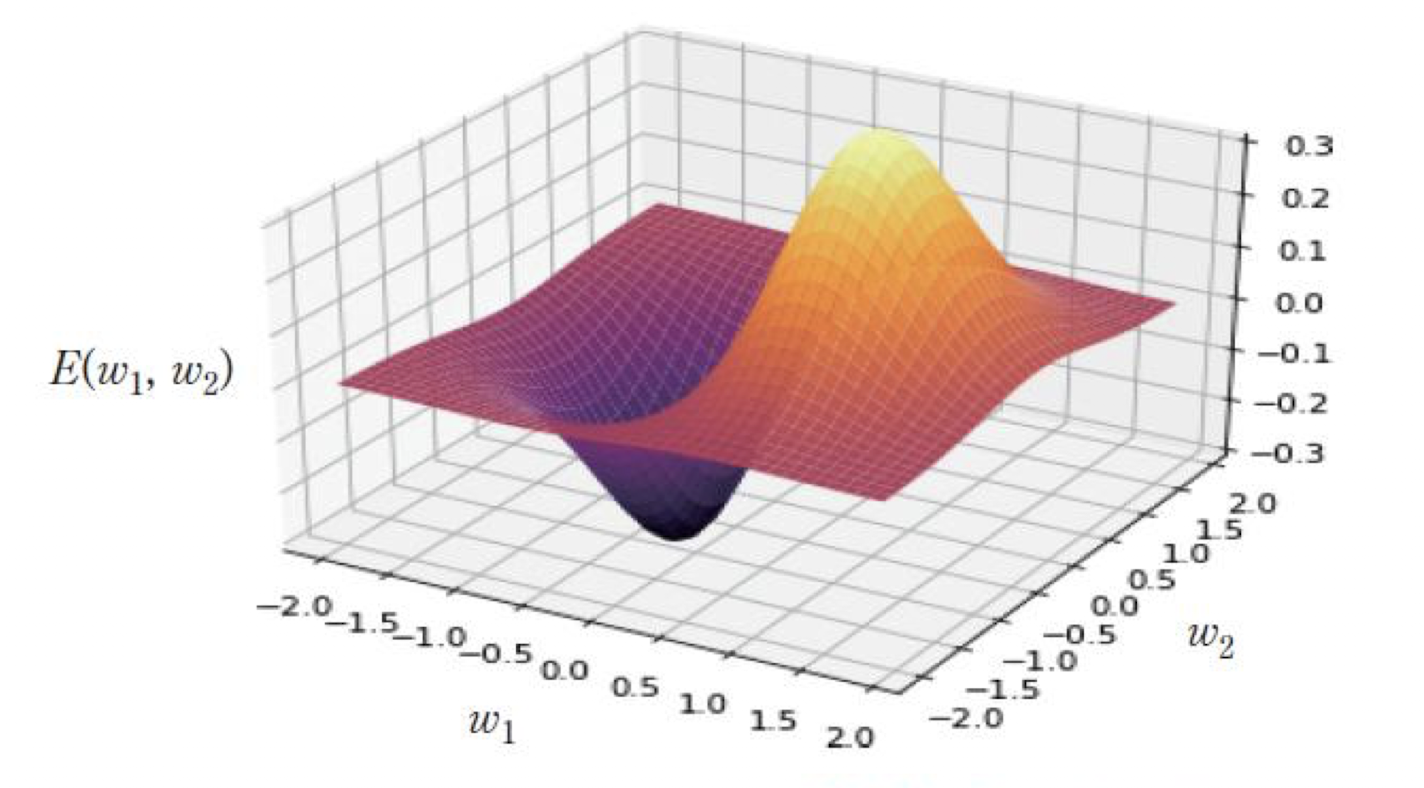
💡 신경망이 정답과의 오차를 가장 작게 만들도록 가중치를 학습하는 것!
✔️ 손실 함수의 그래디언트
로 미분한 값이며 에서 접선의 기울기를 뜻한다.
:
→ 가중치를 증가시키면 오차도 증가
→ 따라서 가중치를 줄이는 방향으로 업데이트
:
→ 가중치를 증가시키면 오차는 감소
→ 따라서 가중치를 늘리는 방향으로 업데이트
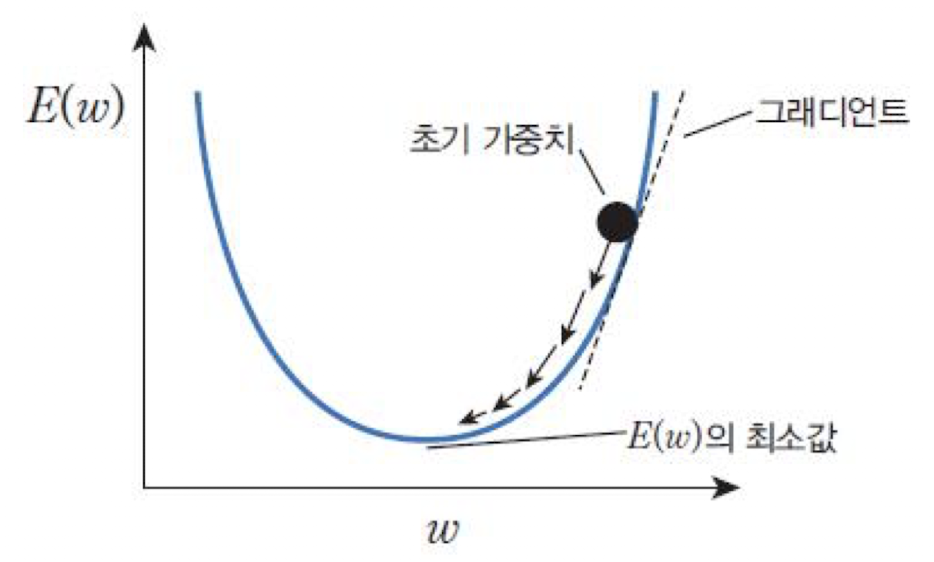
➡️ 오차를 최소화하기 위해 항상 기울기의 반대 방향으로 가중치를 조정!
Loss function:
gradient:
→ loss function: ,
gradient: →
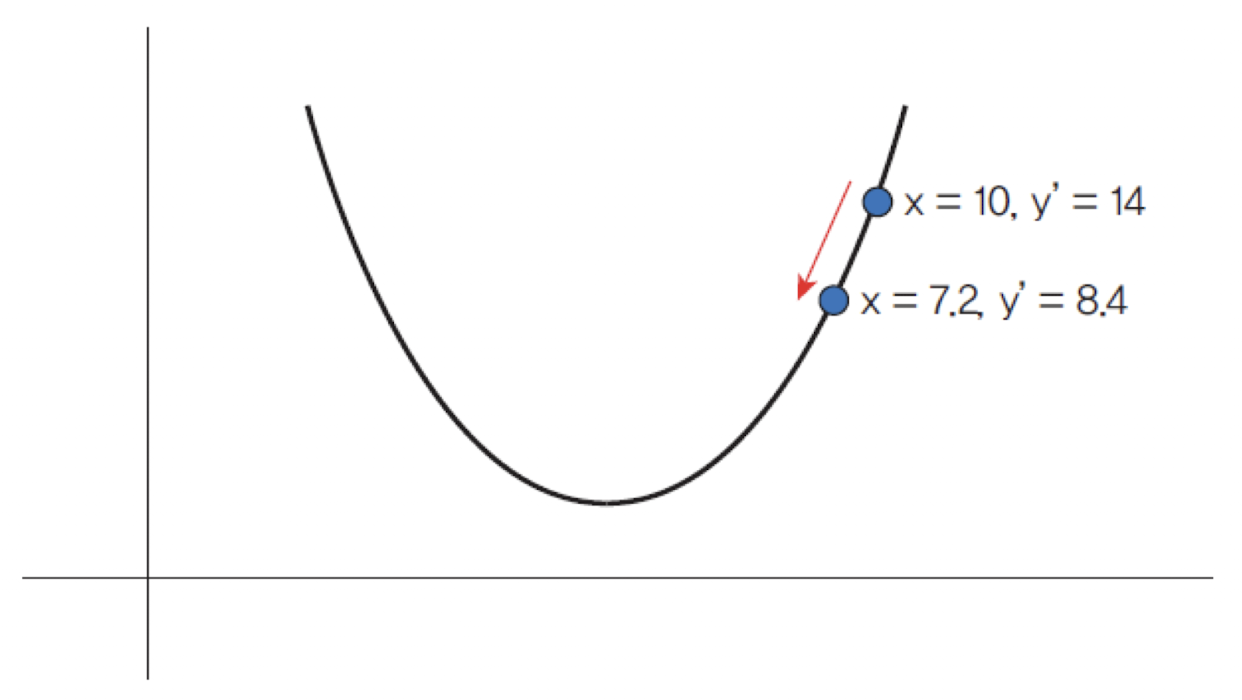
📦 Code
x = 10
learning_rate = 0.2
precision = 0.00001
max_iterations = 100
# 손실함수를 람다식으로 정의한다.
loss_func = lambda x: (x - 3) ** 2 + 10
# 그래디언트를 람다식으로 정의한다.
# 손실함수의 1차 미분값이다.
gradient = lambda x: 2 * x - 6
# 그래디언트 강하법
for i in range(max_iterations):
x = x - learning_rate * gradient(x)
print("손실함수값(", x, ") =", loss_func(x))
print("최소값 =", x)
손실함수값( 7.199999999999999 )= 27.639999999999993
손실함수값( 5.52 )= 16.350399999999997
손실함수값( 4.512 )= 12.286143999999998
손실함수값( 3.9071999999999996 )= 10.82301184
손실함수값( 3.54432 )= 10.2962842624
...
손실함수값( 3.0000000000000004 )= 10.0
최소값 = 3.0000000000000004from mpl_toolkits.mplot3d import axis3d
import matplotlib.pyplot as plt
import numpy as np
x = np.arange(-5, 5, 0.5)
y = np.arange(-5, 5, 0.5)
X, Y = np.meshgrid(x, y) # 참고 박스
Z = X**2 + Y**2 # 넘파이 연산
fig = plt.figure(figsize=(6,6))
ax = fig.add_subplot(111, projection='3d')
# 3차원 그래프를 그린다.
ax.plot_surface(X, Y, Z)
plt.show()
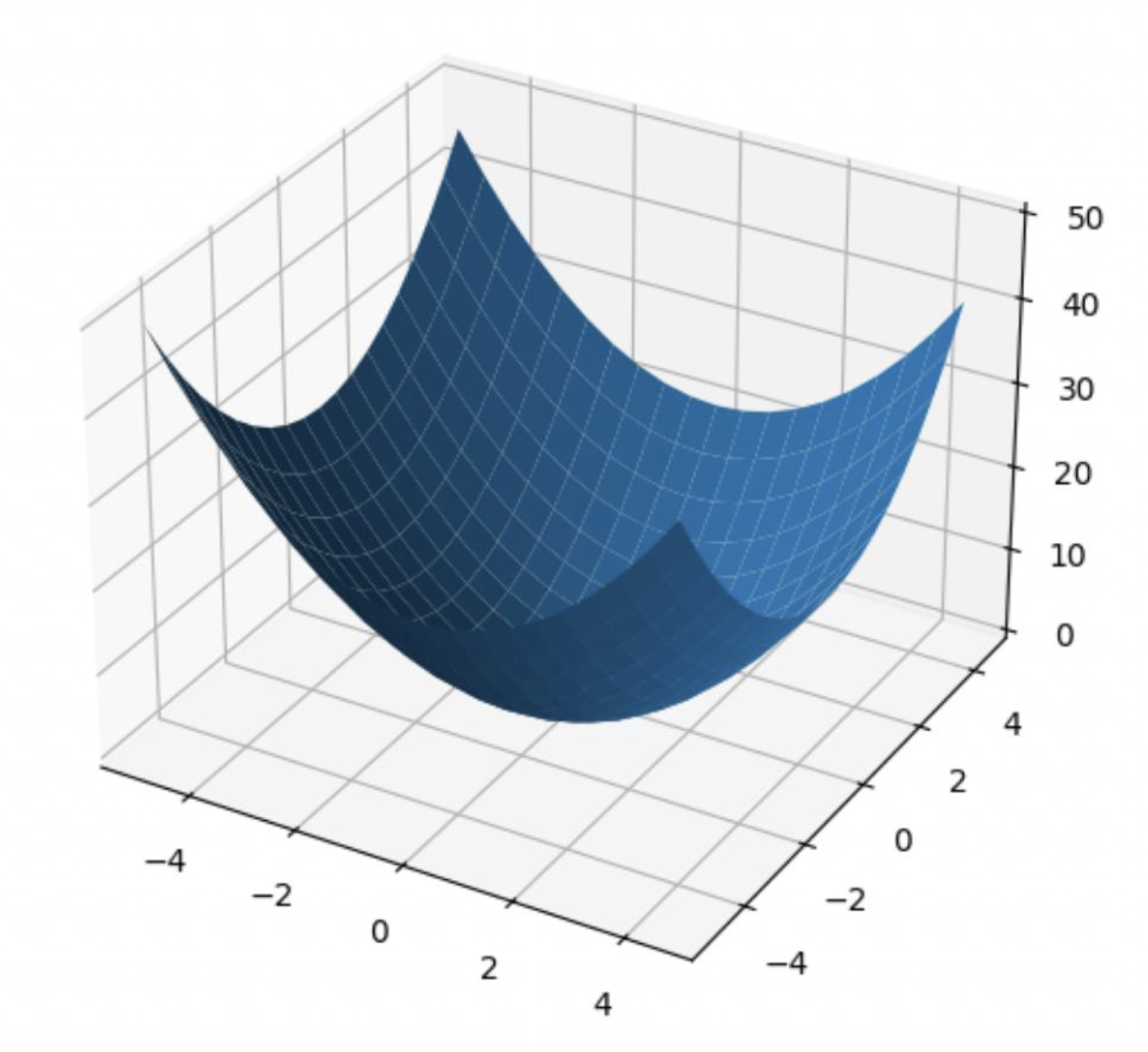
import matplotlib.pyplot as plt
import numpy as np
# x, y 좌표 설정
x = np.arange(-5, 5, 0.5)
y = np.arange(-5, 5, 0.5)
# 2D 그리드 생성
X, Y = np.meshgrid(x, y)
# 함수 f(x, y) = x² + y²의 그래디언트의 반대 방향 계산
U = -2 * X
V = -2 * Y
# 벡터 필드 시각화
plt.figure()
Q = plt.quiver(X, Y, U, V, units='width') # 화살표로 표현
plt.title("Gradient Descent Directions")
plt.grid(True)
plt.show()
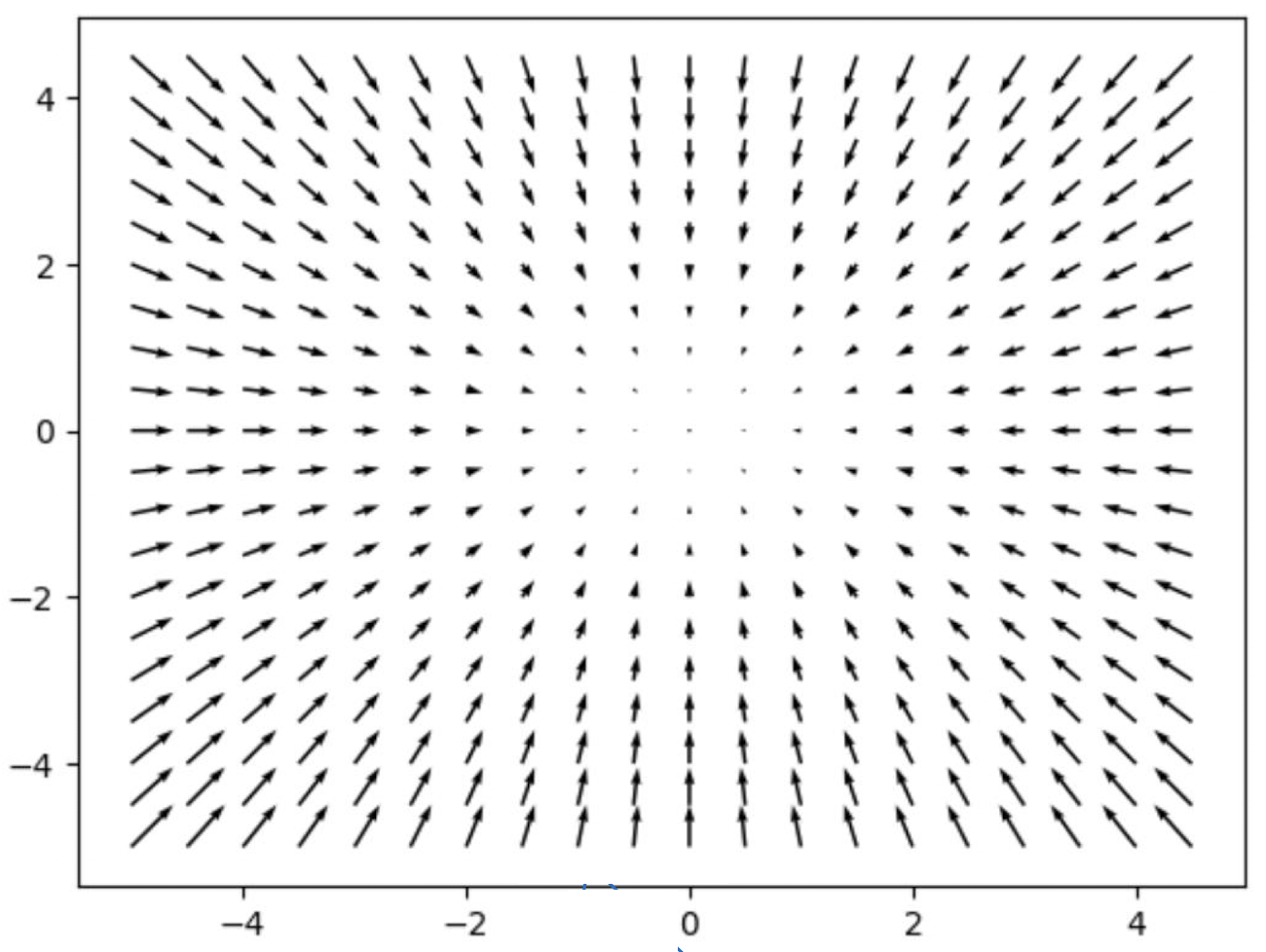
🏷️ 다음내용 "역전파"
다음 포스팅에 역전파 Backpropagation에 대한 내요을 다루겠다.
