저는 아래의 해당 책을 통해 정리하였지만, 해당 책은 수식에 대한 설명 위주라서 서치해서 찾은 자료를 함께 정리하였습니다. 참고 바랍니다.🏃‍♀️

3장 pdf

참고

1. Neural Network
2. Perceptron

앞서 공부했던 Perceptron은 linear classifier라는 한계가 있다. 선형 분리 불가능한 상황에서는 일정의 오류가 발생한다.

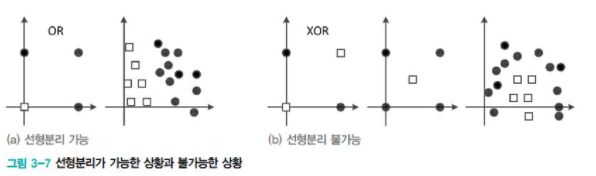
[그림3-7]을 통해 XOR 문제에서는 75%가 정확도의 한계라는 것을 알 수 있다. 이 한계를 지적하고 다층 구조를 이용한 극복 방안을 제시한 것이 Multilayer Perceptron이다. 그 이후 오류 역전파(back propagation) 알고리즘이 제안되었고, 이는 그 다음 포스팅에서 다룰 예정이다.

Multi-layer perceptron

1. Multi-layer Perceptron의 특징

Multilayer Perceptron은 여러 개의 퍼셉트론을 결합한 다층 구조를 이용하여 선형 분리가 불가능한 상황을 해결한다.

1. hidden layer가 있음
   hidden layer는 원래 특징 공간을 분류하는데 훨씬 유리한 새로운 특징 공간으로 변환합니다.
2. sigmoid activation function
   퍼셉트론은 [그림3-3(b)]을 activation function으로 활용하였다. 반면 다층 퍼셉트론은 sigmoid를 사용한다. 여기서는 출력이 연속값인데, 출력을 신뢰도로 간주함으로써 더 융통성 있게 의사결정이 가능하다.

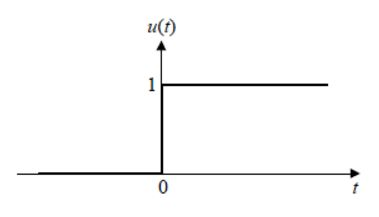
[step function]

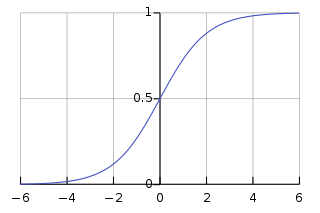
[sigmoid function]

3. back propagation algorithm을 사용한다.
   다층 퍼셉트론은 여러 층이 순차적으로 이어진 구조이므로, 역방향으로 진행하면서 한 번에 한 층씩 gradient를 계산하고 weight를 갱신하는 방식이다.

2. Activation Function

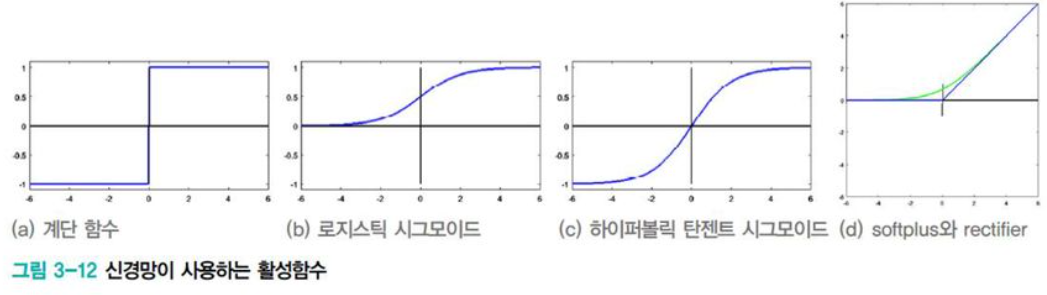
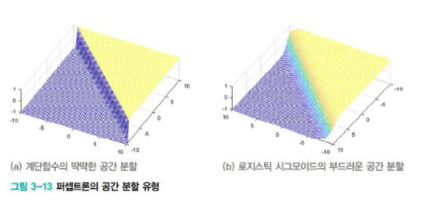
[그림3-12(a)]는 퍼셉트론이 사용하던 step activation function이다. 이 함수의 딱딱한 의사결정을 부드러운 의사결정으로 확장하기 위해서는 [그림3-12]의 (b)~(d)를 사용하면 된다.

[표3-1]을 참고하면 logistic sigmoid나 tanh sigmoid(그냥 sigmoid, tanh라고 더 자주 부른다.)는 매끄러운 곡선 모양이며 미분이 가능하다. 매개변수 α에 따라 기울기가 결정되는데, α가 클수록 가파르며 무한대이면 step function이 된다.

위 함수는 연산이 모두 간단하며 빨리 계산하는 성질을 갖고 있다. (activation function은 한 번 더 따로 정리할 예정이다.)

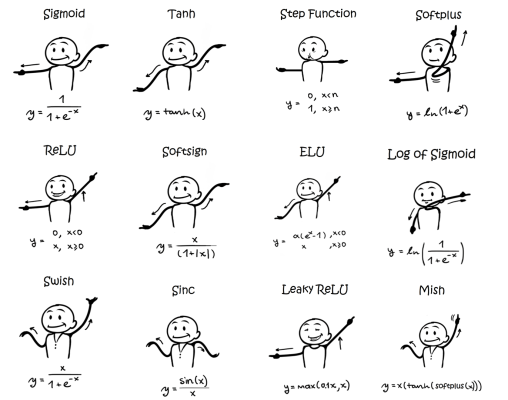
위의 귀여운 이미지를 통해 각 알고리즘마다 사용되는 activaion function을 기억해두면 성질을 파악하기 좋다.

퍼셉트론은 계단 함수를 사용했고, 다층 퍼셉트론은 sigmoid, tanh를 사용하였다. softplus나 ReLU는 뒤늦게 발견되었는데, 이는 딥러닝에서 주로 다루는 내용이다.

왜냐하면 딥러닝이 sigmoid나 tanh를 사용하면 학습 도중 gradient가 점점 작아져 0에 가까워지는 문제가 발생한다. 이를 gradient vanishing이라고 한다. 이때 ReLU를 사용하면 문제가 완화된다.

또한 ReLU는 비교 연산이기 때문에 속도 향상에 많은 기여를 한다. 하지만 음수를 모두 0으로 대체하기 때문에 문제가 또 발생한다. 이 해결 방법은 경사하강법(Gradient descent) 이고 아마 딥러닝을 공부했다면 한 번쯤은 들어봤을 법한 개념이고 꽤 중요하게 다룬다!

3. 구조

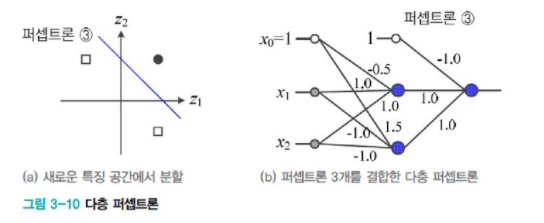
[그림3-10]은 XOR 분류 문제를 푸는 간단한 MLP이다. 이를 일반화한 구조는 아래와 같다.

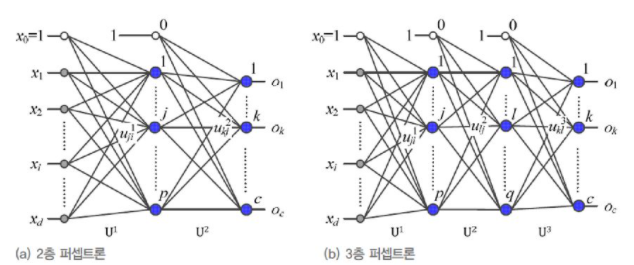
일벽층과 출력층에 놓인 새로운 층을 hidden layer라고 한다.

입력층은 주어진 feature vector를 입력하는 곳, 출력층은 neural network의 최종 출력이 나오는 곳이다. 두 곳 모두 값을 관찰할 수 있지만, hidden layer는 계산의 중간 과정이 보이지 않아 hidden이라는 이름이 붙었다. 여기서 퍼셉트론과 층이 여러 개여서 Multi-layer라는 이름이 붙었다.

[그림3-14(a)]는 은닉층이 하나인 다층 퍼셉트론이다. 입력층, 은닉층, 출력층 3개지만 입력층은 배제하기 때문에 2층 퍼셉트론이 되고, [그림3-14(b)]는 은닉층이 두 개인 다층 퍼셉트론이라 3층 퍼셉트론이라 부른다.

입력층에는 특징 벡터 x = (x1, x2, ..., xd)T를 받으려고 d개의 노드가 있다. 실제로는 1이 입력되는 bias 노드를 추가하여 d+1개의 노드가 있다.

출력층에는 c개의 노드가 있는데, 분류 문제에서는 부류의 개수에 해당한다.(class 개수) 예를 들어, iris datset이라면 c는 3, mnist 숫자 인식에서는 c가 10이다.

다시 말해, train set가 무엇인지 결정되면 Multi-layer perceptron 구조 중 입력 노드와 출력 노드의 개수는 자동으로 정해진다.

반면, hidden layer에 있는 노드의 개수 p는 사용자가 지정해야하는 하이퍼 매개변수(Hyper parameter)이다. 앞서 p는 Multi-layer perceptron의 용량을 규정한다고 했는데, 너무 크면 과잉적합, 너무 작으면 과소적합의 위험이 있으므로 적절한 값을 선택해야 한다.

parameter

2층 퍼셉트론의 parameter는 입력층과 hidden layer를 연결하는 weight가 있고, hidden layer와 출력층을 연결하는 parameter가 있다.

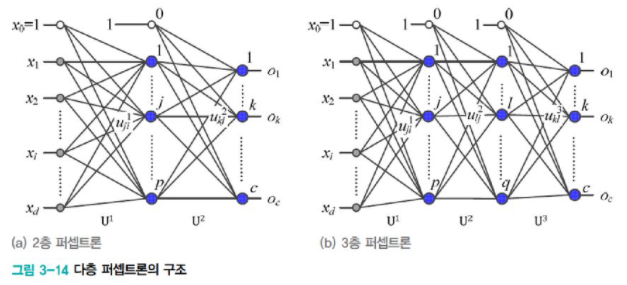
[그림3-14(a)]에서는 이들을 U1, U2라 표기하였다. U, V라 표기하여 구분할 수 있지만, 여러 개의 hidden layer를 쉽게 확장할 수 있도록 U1, U2라 표기한다.

이를 식으로 표현하면

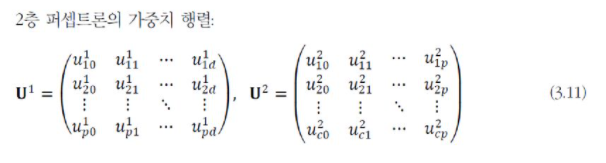
위와 같다.

여기서 한 가지 보고 가야하는 건, i번째 노드와 j번째 노드를 연결하는 가중치가 u_ji로 표기된다는 점이다. 몇 번째 층에 해당하는 가중치인지 표시된다.

4. 동작

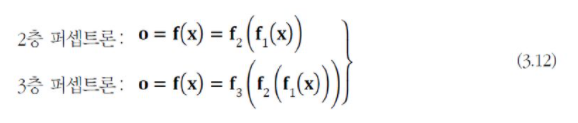
Multi-layer perceptron 동작은 벡터 x를 벡터 o로 매핑하는 함수이다.

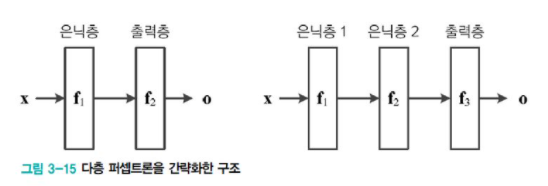
위의 그림이 식의 매핑 과정을 설명한다.

여러 퍼셉트론을 결합한 구조인 만큼, 연산도 연달아 일어나는 방식이라 이해하면 쉽다. 책에 나오는 자세한 수식 설명은 생략하겠다.

궁금하다면 위의 이미지를 참고하면 된다.

hidden layer의 역할

이쯤되면 hidden layer가 무엇을 하는지 의문이 들 것이다.

hidden layer는 원래 feature space를 새로운 feature space로 변환하는 feature extractor이다. 즉, hidden layer는 feature을 추출한다.

기계 학습에서는 이를 feature learning이라 한다. 딥러닝은 더 많은 단계를 거쳐 feature learning한다.

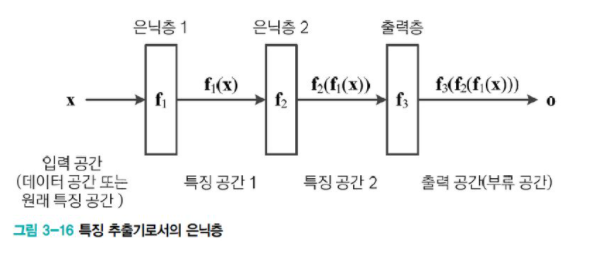
그렇다면 어떻게 f1, f2를 설정해야 우수한 feature space를 만들 수 있을까? 은닉층이 많은 깊은 신경망이어야 더 잘 학습하지만, 해당 책은 딥러닝을 이해하기 전 은닉층이 하나 뿐인 neural network의 예로 이해를 강조한다.

그 뒤에 다룰 내용은 Back Propagation과 Gradient Descent이다.