저는 아래의 해당 책을 통해 정리하였지만, 해당 책은 수식에 대한 설명 위주라서 서치해서 찾은 자료를 함께 정리하였습니다. 참고 바랍니다.🏃♀️

참고
Multi-layer Perceptron(다층 퍼셉트론)은 hidden layer 덕분에 선형분리가 불가능한 상황도 처리할 수 있는 용량을 갖게 되었다. 용량이 커질수록 추정해야 할 매개변수가 많아진다.
1969년 Multi-layer Perceptron 구조가 제안되었지만 회의적인 견해를 받았던 이유도 많은 매개변수를 추정할 마땅한 학습 알고리즘이 당시에 없었기 때문이다.
하지만 1986년에 back propagation이라는 효율적인 학습 알고리즘이 탄생한다. 이 알고리즘은 신경망 연구를 부활시켰으며, 현재 기계 학습에서 대세인 딥러닝의 모델이 된다.
1. 목적함수의 정의
훈련집합이 X = {x1, x2, ..., xn}과 부류 벡터 집합 Y = {y1, y2, ..., yn}이 있다. 소속 부류가 j번째이면 y_i = (0,0,...,1,...,0)T이다. 즉, j번째 요소만 1이고 나머지는 0인 원핫 코드로 표현된다.
만일 하이퍼볼릭 탄젠트(tanh)와 같이 범위가 (-1,1)인 activation function을 사용한다면 0을 -1로 바꾸면 된다.
이를 행렬로 표기하면 X와 Y는 nd와 nc 행렬이다. n은 sample의 개수, d는 feature vector의 차원, c는 class의 개수이다.
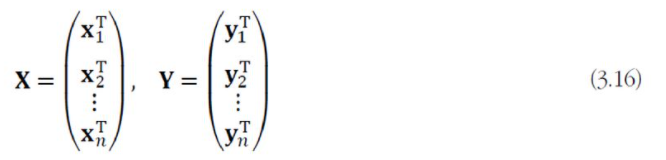
기계학습의 목표는 모든 sample을 옳게 분류하는 최적의 함수 f를 알아내는 것이다. 하지만 현실적으로 불가능하므로, 대부분 현실과 타협해 근사 최적해를 찾아낸다.
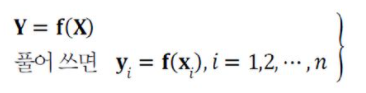
기계 학습은 multilayer perceptron의 출력 f(X; θ)와 주어진 class 정보인 Y의 차이를 최소화하는 최적의 매개변수 θ-hat을 찾아야 한다.
Stochastic gradient descent는 하나의 샘플에 대해 gradient를 계산하고 바로 weight를 갱신하는 방식이다. Batch gradient descent는 모든 sample의 gradient를 계산한 후에 한꺼번에 weight를 갱신하는 방법이다.

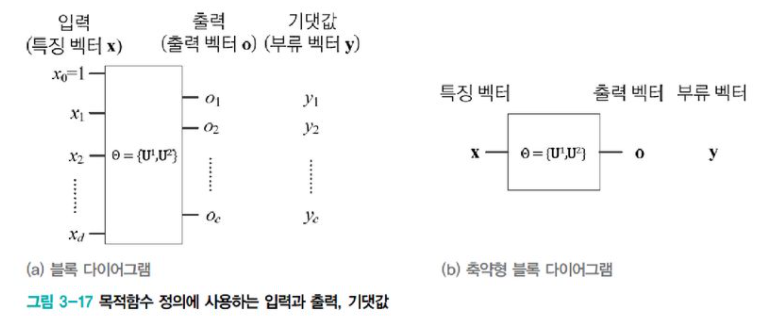
[그림3-19]가 [식3.19]를 보충 설명한다. neural network의 구조를 block으로 추상화하였고, 추정해야 할 매개변수 θ = {U1, U2}를 표시하였다. 특징 벡터 x가 입력되면 [식3.15]에 따라 feed forward 계산을 수행하여 출력 o를 얻은 다음 [식3.19]의 목적함수를 적용하여 x의 class vector와 출력 o의 평균제곱 오차(MSE, mean squared error)를 계산한다. 미분할 때 상수항을 1로 유지하여 수식 표현을 간단하게 하려고 1/2을 곱해준다.
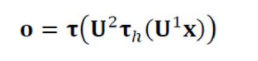
[식3.15]
MSE는 주로 multi-layer perceptron이 사용하는데, 딥러닝은 Cross Entropy Error, Log Likelihood를 사용한다.
딥러닝은 multi-layer perceptron보다 획기적인 성능 향상을 보여 주는데, 이 새로운 목적함수들도 성능 향상에 도움을 준다.
2. back propagation 알고리즘 설계
[식3.19]에서 수식을 매개변수 θ가 드러나도록 다시 쓰면 [식3.20]이 된다. θ의 값에 따라 출력이 정해지므로 o를 o(θ)로 표기했으며, MSE도 e 대신 J(θ)로 표기된다.

기계학습 알고리즘은 [식3.20]의 목적함숫값이 줄어드는 방향으로 θ, 즉 U1과 U2의 값을 수정해야 한다. gradient descent원리에 따라 [식3.21]이 성립된다.

back propagation 유도 과정
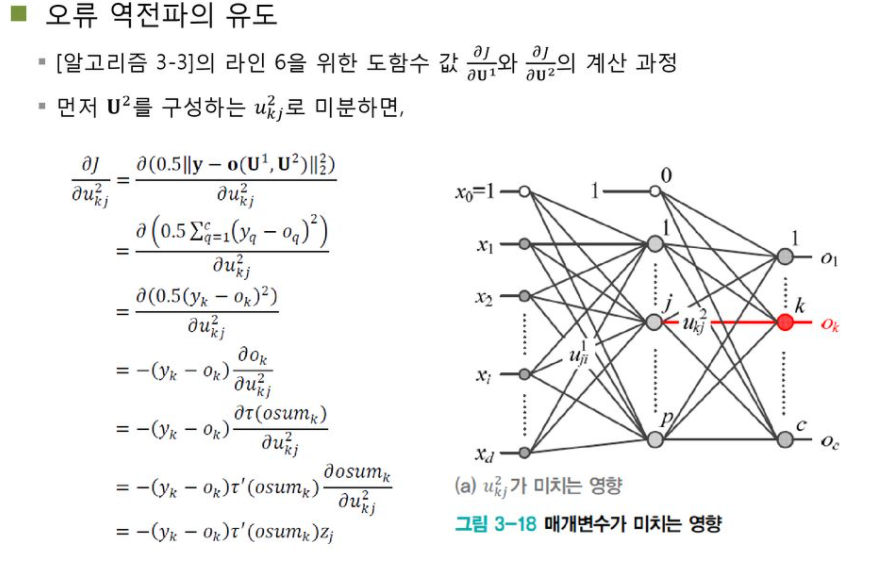
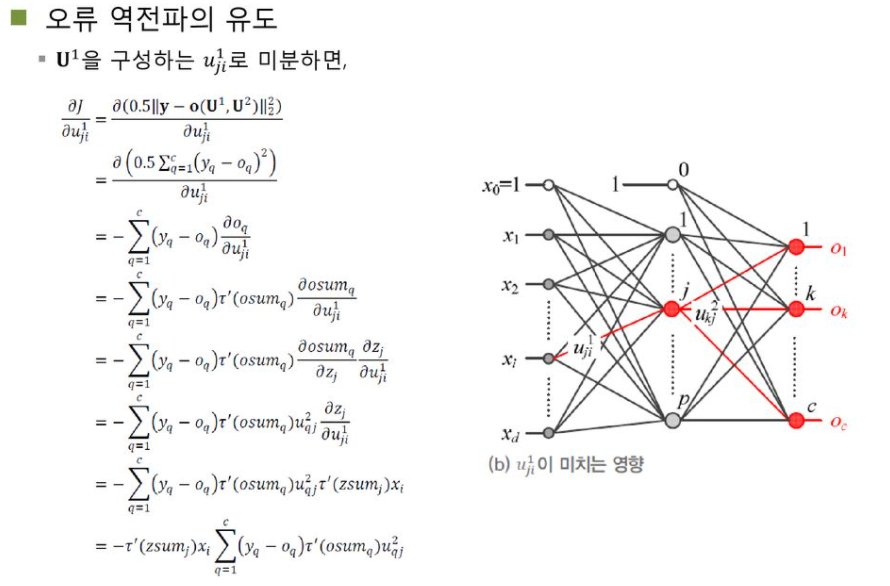

유도 과정은 해당 ppt를 참고하시길 바랍니다!
back propagation은 out layer를 역방향(왼쪽)으로 전파하며 gradient를 계산하는 알고리즘이다.
3. back propagation의 한계
back propagation은 경사 하강법의 한계에서 오는 건데, 항상 전역 최솟값인 global minimum을 찾는다고 보장할 수 없다는 것이다.
극솟값이 두 개 이상 존재하는 함수에 대해 가장 작은 최솟값을 찾는다고 할 수 없다. 알고리즘이 단순히 기울기가 작아지는 방향으로 움직이는 것이라서 시작점에 따라 결과도 달라진다.
