0. 목차
- Perceptron
- 경사하강법
- 경사하강법
- 편미분
- Local Minimum
- 데이터 처리
1. 경사 하강법
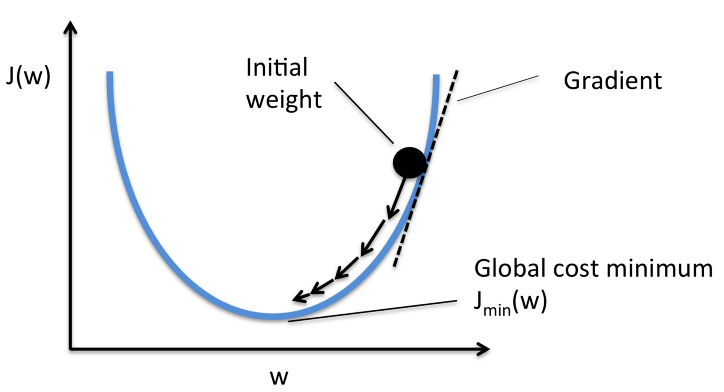
- 미분계수를 이용해 함수의 최솟값을 찾아가는 방법
- Loss가 최소가 되는 지점(W)을 찾아가는 방법
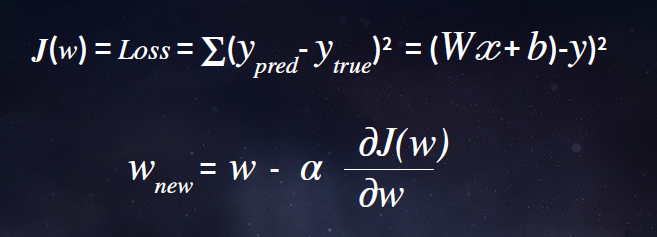
Loss는 예측한 값에서 실제 값을 뺀 값의 제곱을 의미합니다.
2. 편미분
- 미분은 접선의 기울기
이다.
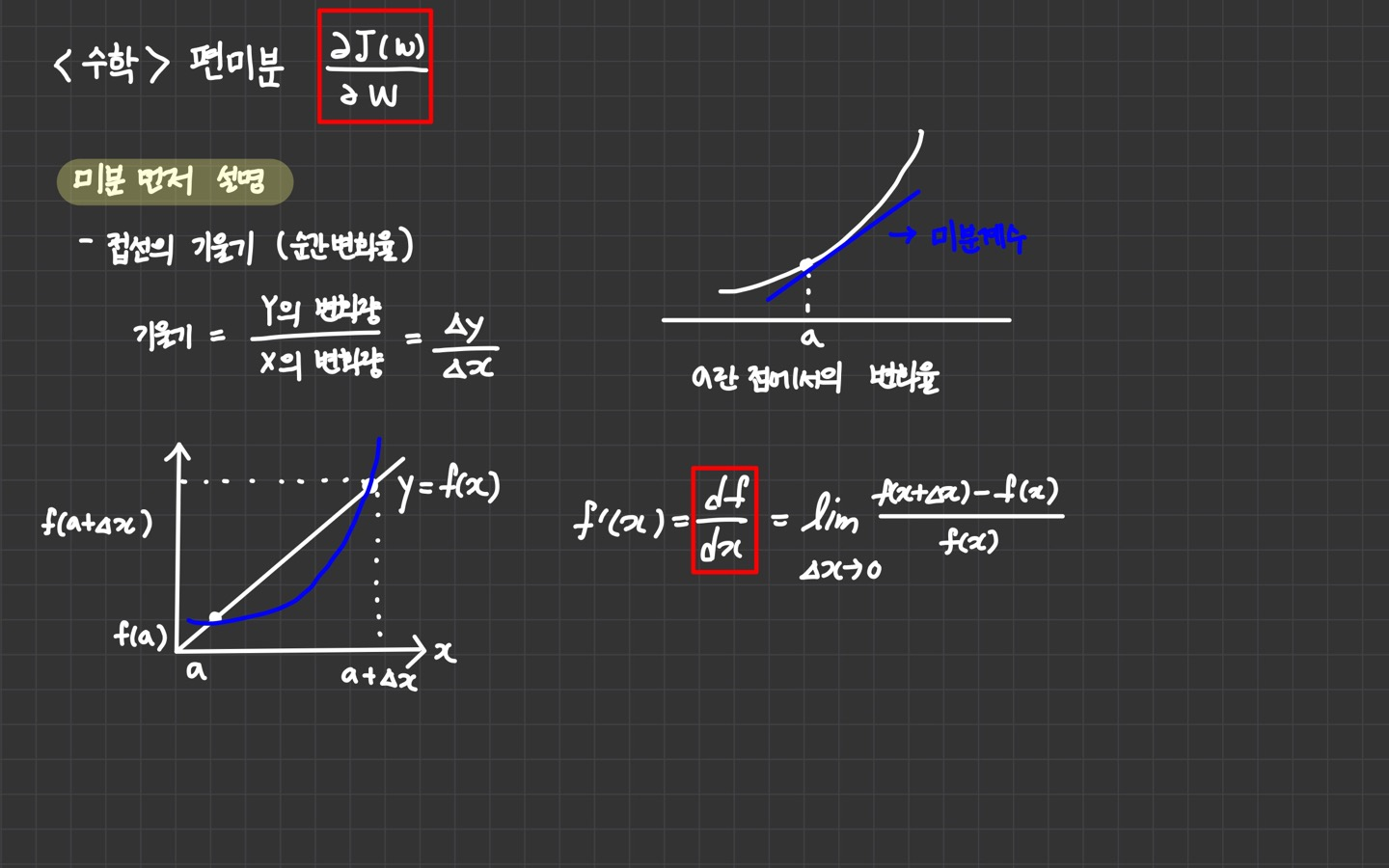
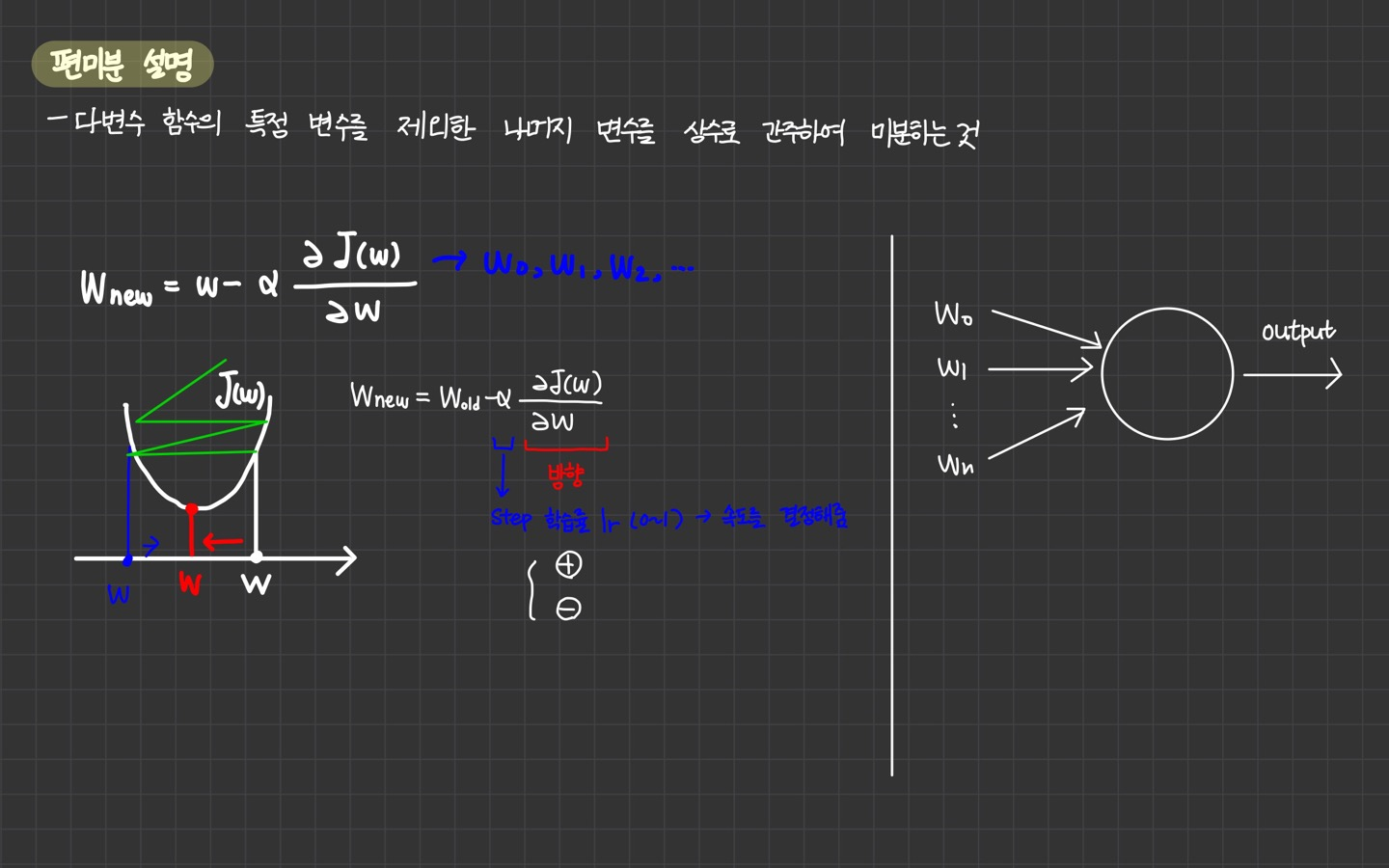
- 편미분은 다변수 함수의 특정 변수를 제외한 나머지 변수를 상수로 간주하여 미분하는 것
3. Local Minimum
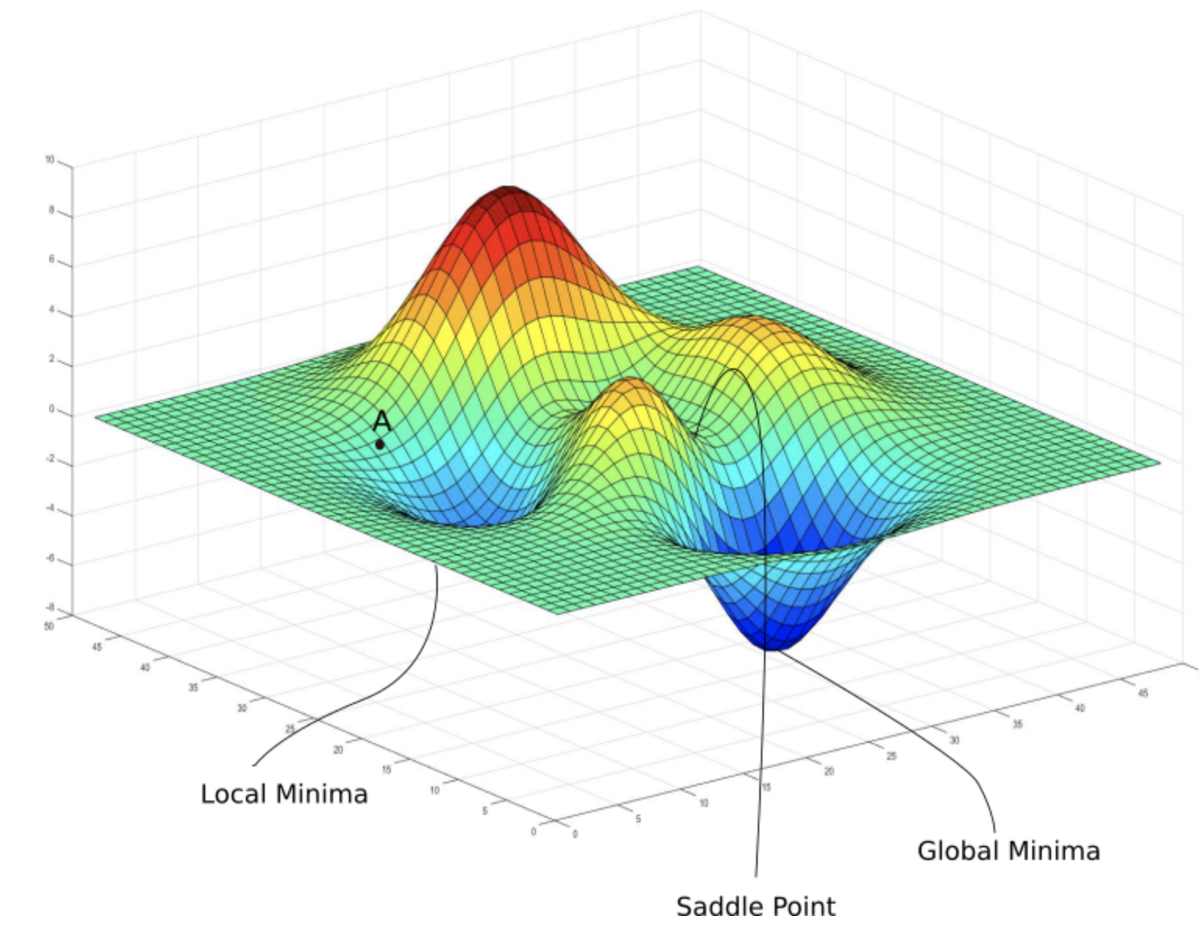
위의 그림을 살펴보면 Local minimum과 Global Minima가 나온다.
이를 2차원 평면에서 다시 그리면
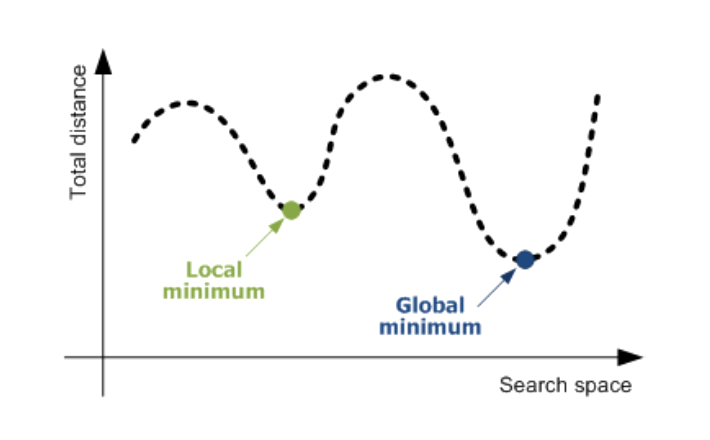
해당 그래프로 표현이 될 수 있다.
y값이 가장 낮은 부분이 Global Minima에 해당되고, 미분계수(접선의 기울기)가 0인 부분이 Local minimum에 속하게 된다.
우리가 도달해야하는 곳은 Global Minima인데, 어떤 w 값(가중치)은 Loss Function이 가장 낮은 구간(Global Minima)이 아니라 Local minimum에 도달하게 된다.
그래서 빠지게 되는 문제를 Local Minimum 문제라고 한다.
정리하면
w(가중치) 값의 시작점에 따라 Local minimum에 빠질 수 있다.

안녕하세요 글 잘 보고 있어요..!
제가 요즘 많이 고심하는데도 모르겠어서
여쭤보고 싶은 공업수학 문제가 있는데
혹시 답변 해주실 수 있으실까요..?
곤란 하시다면 답변 안 해주셔도 괜찮아요
문제는 이거예요…!
“분리가능 상미분 방정식은 양형태 상미분 방정식의 일부이고, 완전 상미분 방정식은 음형태 상미분 방정식 일부라고 볼 수 있다.
양형태의 상미분 방정식 중 분리가능한 상미분 방정식을 제외하고 남은 상미분 방정식들은 어떤 것들이 있는지 (즉, 분리가능하지 않은 상미분 방정식들), 음형태의 상미분 방정식 중 완전 상미분 방정식을 제외하고 남은 상미분 방정식들은 어떤 것들이 있는지 (즉, 완전하지 않은 상미분 방정식들) 쓰시오.
즉.
양형태의 상미분 방정식의 전체 집합을 W.
음형태의 상미분 방정식의 전체 집합을 U,
분리가능한 상미분 방정식의 전체 집합을 A,
완전 상미분 방정식의 전체 집합을 B
라고 할 때
집합 A^c ᑎ W 과 집합 B^c ᑎ U 에 대해 기술하는 문제이다. 그 집합에 해당하는 미분 방 정식의 예를 몇 개 구하고 그들의 공통된 특징을 기술하는 방법을 써도 좋고, 아니면 이 집 합에 속하는 방정식들의 특징을 바로 기술하여도 좋다.“