[DL] 퍼셉트론 - Linear Model, Activation Function

0. 목차

1. Perceptron
   • Linear Model
   • Perceptron
   • Activation Function
2. 경사하강법
3. 데이터 처리

딥러닝의 구성 요소

Data - Model - Output

1. Linear Model

1. 회귀(Regression)

2. 분류(Classification)

독립변수	종속변수	Task
습도, 풍속, 월, 미세먼지, 자외선지수	온도	회귀
지역 인구수, 매매량, 가구수	집값	회귀
제목, 본문내용, 메일주소	스팸메일 여부	분류
생산연도, 산도, 속성기간, 품종, 당도	와인 등급	분류

• Data: 독립변수
• Output: 종속변수

분류의 output 값은 개수를 정할 수 있다.

모델의 성능

• Linear model로 가정한다.(=데이터가 직선으로 표현할 수 있다)

$y = ax + b$

• 데이터를 가장 잘 설명해주는 a와 b를 찾는다.(a는 기울기, b는 절편)
• Loss가 최소가 되는 a와 b를 찾는다.

$Loss=Σ(y_{pred}-y_{true})^2$

2. Perceptron

• 1956년 Frank Rosemblatt에 의해 제안
• 인간의 신경망 구조를 도식화
• 가장 간단한 인공 신경망 구조

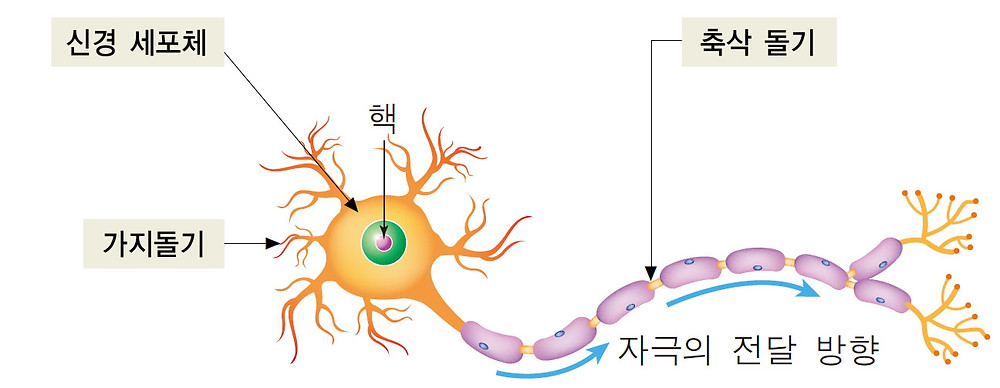
[Neuron의 구조]

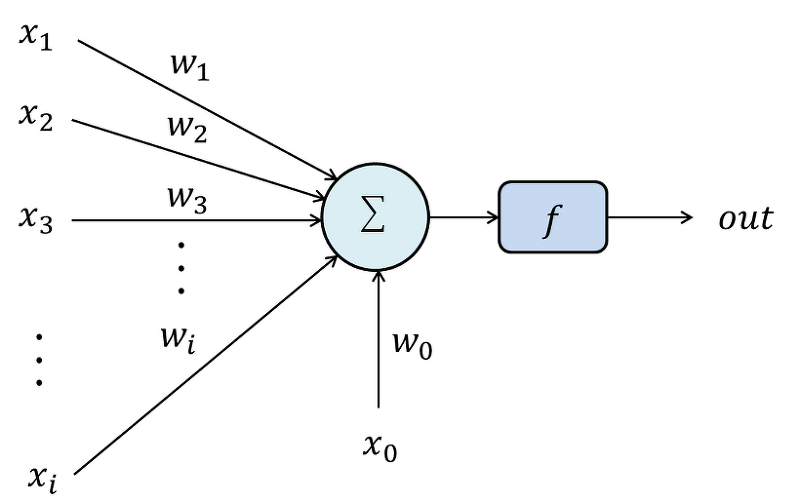
[McCulloch and Pits Model, 1943]

Perceptron의 구성요소

• 입력층, 은닉층, 출력층이 존재
• 데이터를 받아들이는 입력층, 입력층의 정보를 결합해 전달하고 출력층에서 결과값을 도출

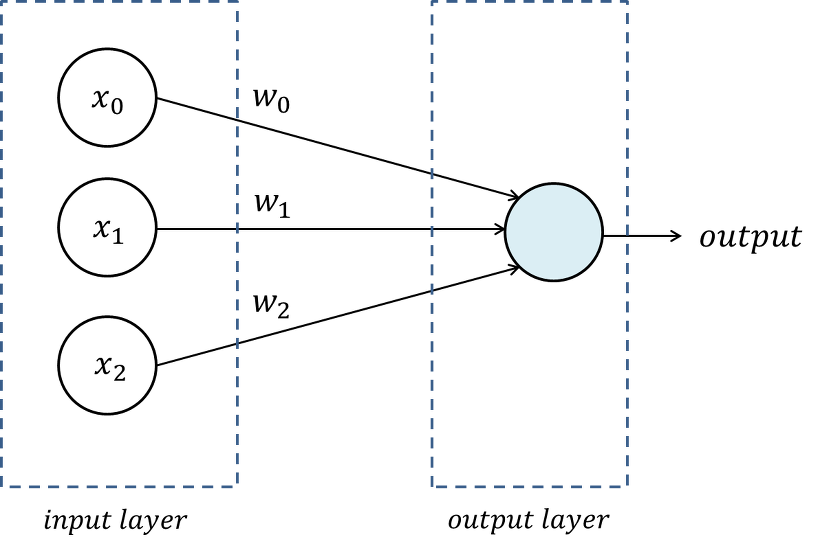
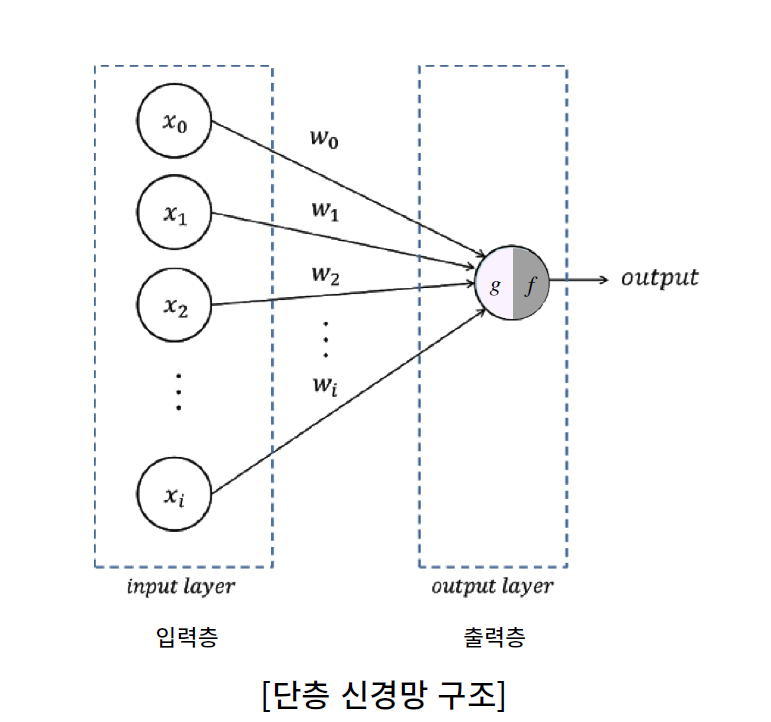
입력층 - 출력층

[단층 신경망 구조]

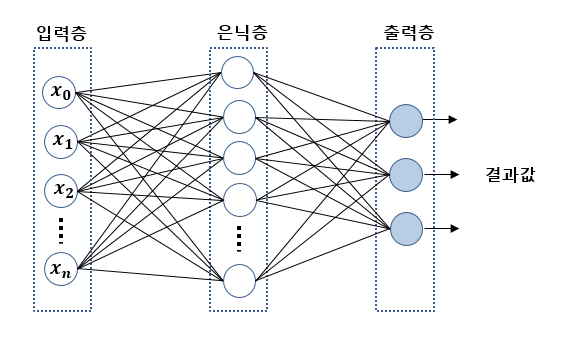
입력층 - 은닉층 - 출력층

[다층 신경망 구조]

• 입력층: input layer
• 은닉층: hidden layer
• 출력층: output layer

Perceptron의 구성 요소

$y_0 = w_0x_0+b_0$
$y_1 = w_1x_1+b_1$
...

$g(x)=$ $y_0$ + $y_1$ ...

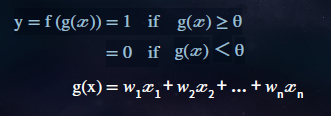
데이터 예시

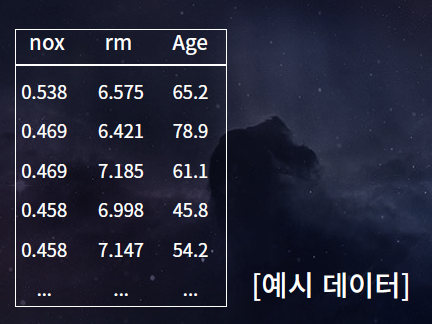
여기서 nox, rm, Age는 data 정보의 관점에서 feature라고도 하고, 행렬의 관점에서 column이라 부르기도 한다.

행으로 이루어진 것은 sample이라 생각하면 된다.

위의 식에서 0.538의 값은 $x_0$, 6.575의 값은 $x_1$, 65.2의 값은 $x_2$로 생각하면 된다.

3. Activation Function

활성화 함수(Activation function)

• f → 활성화함수(Activation function)
• non-linear 하다.

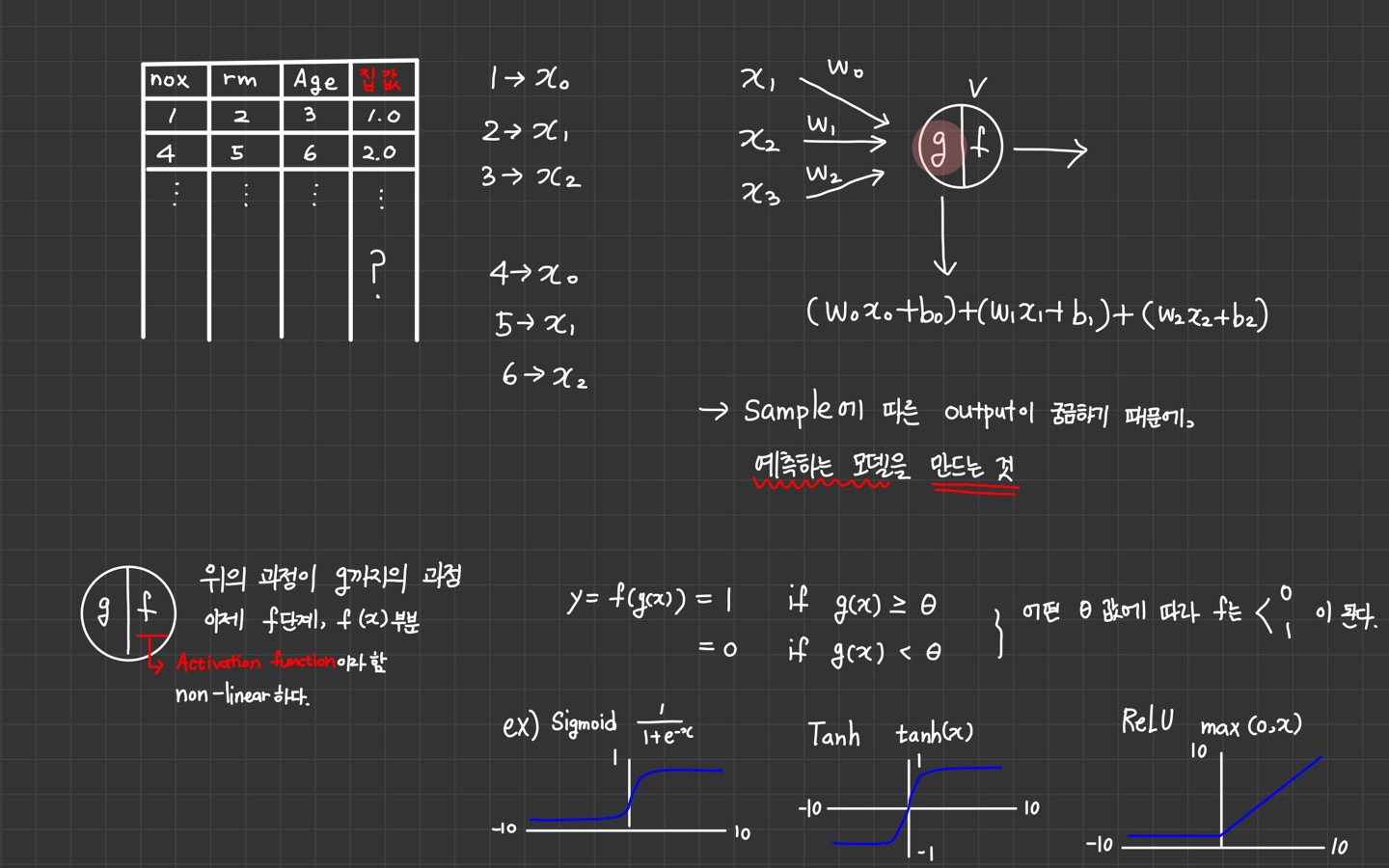
예시

• sigmoid
• Tanh
• ReLU

만약 g(x)를 sigmoid 함수에 집어 넣으면 0 또는 1의 값이 나올 것이다.

하지만 이건 regression 문제이기 때문에 0과 1로 나뉘는 것보다 다른 함수를 쓰는게 더 적절할 것이다.

이제 모델이 예측한 값 $a$가 있다고 하면, 그 값을 $y_{pred}$ 라고 한다.

그리고 실제 값을 $y_{true}$라고 한다면,

$(y_{pred}$ - $y_{true})^2$ 이 $Loss$ 값이 된다.

$(y_{pred}$ - $y_{true})^2 = Loss$