저는 해당 책과 ppt 자료를 바탕으로 포스팅하였습니다. 자세한 내용은 책과 ppt 자료를 참고하시면 감사하겠습니다.

이전 참고 글
선형 회귀 문제
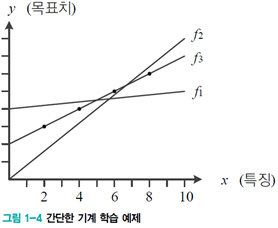
[그림1-4]의 예제는 직선 모델을 사용하여 회귀 문제를 풉니다. 이러한 기계 학습 알고리즘을 linear regression이라고 합니다.

linear regression은 위의 [식1.2]의 직선 모델을 사용하므로 추정해야 할 매개변수는 w와 b, 2개이다. 이 매개변수를 묶어서 Θ=(𝑤,𝑏)T이라 표기한다.
목적 함수(objective function)
처음에는 최적의 매개변숫값을 알 수 없으므로 난수를 생성하여 Θ1=(𝑤,𝑏)T가 되었다고 가정한다. Θ1을 개선하여 Θ2, Θ2를 개선하여 Θ3을 얻는 방식을 반복해 결국 최적의 매개변수 Θ-hat에 도달해야 한다.
이때 직선을 움직이기 위하 필요한 것이 목적함수(objective function)이라 하고 또는 비용 함수(cost function)라고 한다.
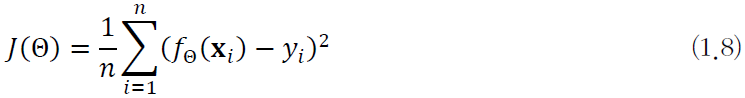
위 [식1.8]이 linear regression을 위한 cost function이다.
- 𝑓_Θ는 Θ를 매개변수로 가지는 직선을 의미하고, f(x;Θ)로 표기하기도 한다.
- 𝑓Θ (𝐱𝑖)는 예측함수의 출력이다.
- yi는 예측함수가 맞추어야 하는 목푯값이다.
- 𝑓Θ (𝐱𝑖)-yi는 xi에서의 오차이며, 이 식을 평균제곱오차(MSE, mean squared error)라고 부른다.
[예제 1-1] 풀어보기
train set은
- 𝕏={𝑥_1=(2.0),𝑥_2=(4.0), 𝑥_3=(6.0), 𝑥_4=(8.0)},
- 𝕐={𝑦_1=3.0, 𝑦_2=4.0, 𝑦_3=5.0, 𝑦_4=6.0}
이다. 초기 직선의 매개변수 Θ1 = (0.1, 4.0)T라 설정하고 J(Θ)에 대입하면,
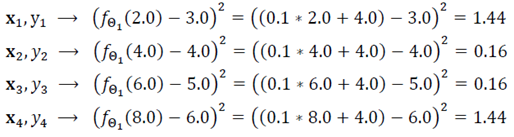
해당 값이 나온다. 계산하면 𝐽(Θ_1)은 0.8이 나온다. 이제 Θ_1을 개선하여 Θ_2=(0.8,0.0)T가 되었다고 가정한다.
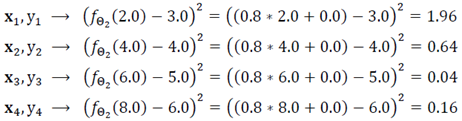
그러면 대입한 식이 위와 같이 나오고 𝐽(Θ_2)는 0.7의 값이 나온다. Θ_2는 Θ_1보다 0.1만큼 목적함수의 값이 줄어 오차가 개선되었음을 알 수 있다.
다시 Θ_2를 개선하여 Θ_3=(0.5,2.0)T가 되었다고 가정한다. 이때 𝐽(Θ_3)=0.0이 되어 Θ_3은 최적값 \ Θ ̂이 된다.
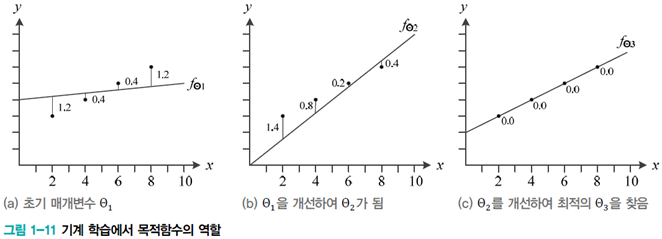
여기서 찾은 Θ_3을 최적의 매개변수 Θ^에 대입하고 학습을 마치면 된다. 이렇게 기계학습이 하는 일을 공식화하면

[식1.9]가 된다. 기계학습 알고리즘은 cost function이 작아지는 방향을 찾아 매개변숫값을 조정하는 일을 반복하는데 0.0 또는 0.0에 아주 가까운 값으로 수렴하면 학습을 마친다.
사실 위의 예제는 아주 간단한 linear regression이므로 굳이 이 방법 대신에 cost function을 매개변수 w로 미분하여 도함수가 0이 되는 수식을 전개해 최적값을 구할 수 있다.
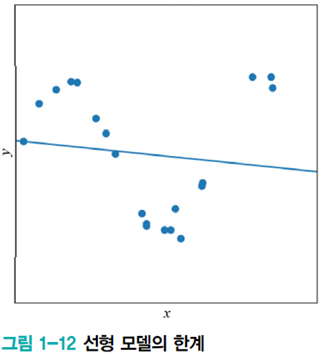
linear model의 한계
지금까지는 데이터가 선형을 이루는 아주 간단한 상황만을 고려하여 매개변숫값을 찾았다. 하지만 실제는 선형이 아니고 잡음이 섞인 데이터가 많다. 데이터에 직접 근사를 하면 아래 [그림1-12]처럼 최적해를 찾더라도 적지 않은 error가 발생한다. 이런 경우에는 비선형 모델이 필요하다. 이는 다음에 다루도록 하겠다!