저는 해당 책의 내용을 보고 정리하였으며 ppt 자료는 아래에 링크 첨부해두었습니다.

Preview
강화학습(reinforcement learning)의 핵심은 좋은 policy를 찾아내는 것이다. 좋은 policy가 있으면 누적 reward를 최대로 만들 최적 action을 매 순간 선택할 수 있기 떄문이다.
강화학습에서 좋은 policy를 찾는 것은 지도학습에서 목적함수의 optimum을 찾는 일에 비유할 수 있다. SGD를 이용해 optimum을 찾아가듯이 강화학습도 적절한 최적화 알고리즘을 사용하여 최적의 policy를 찾아야 한다.
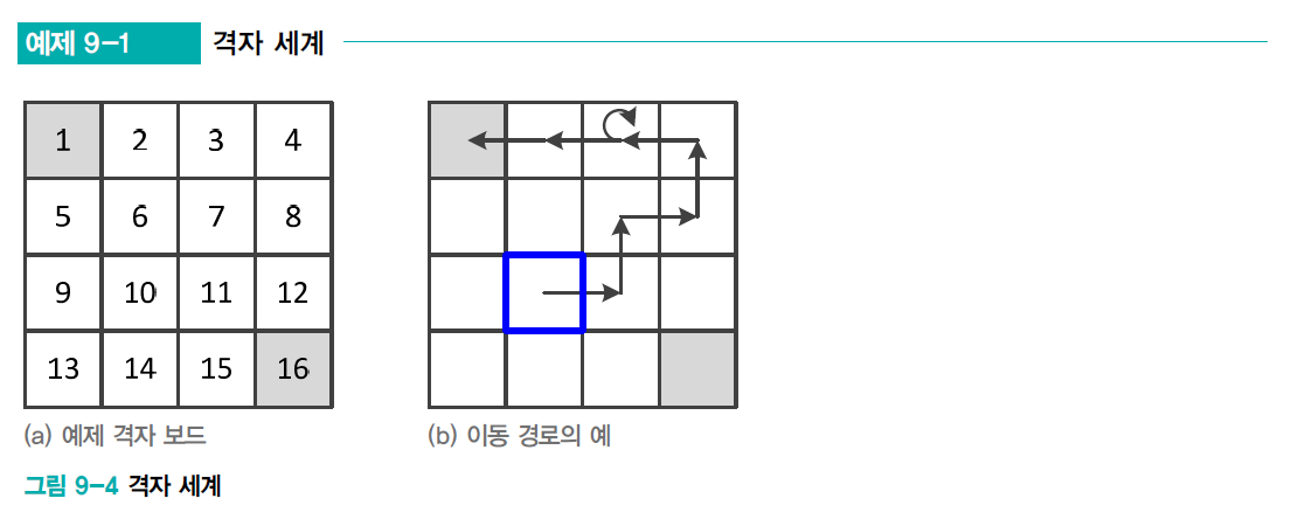
해당 grid처럼 좋은 policy를 찾는 것이 간단하지는 않다. grid가 1000*1000이 될 수 있고, 목표 지점이 흩어져 있거나, 함정이 있을 수도 있다.
좋은 policy란 누적 reward를 최대화하려고 일부러 함정에 빠지는 행동까지 추론할 수 있어야 한다.
해당 포스팅은 policy space가 너무 방대하여 직접 찾는 방법은 무모하고, 이를 도와주는 value function을 소개한다.
1. policy
policy는 𝜋로 표기하고, state s, action은 a이다.

위 식은 정책 𝜋는 상태 s에서 행동 a를 취할 확률을 명시한 것이다.
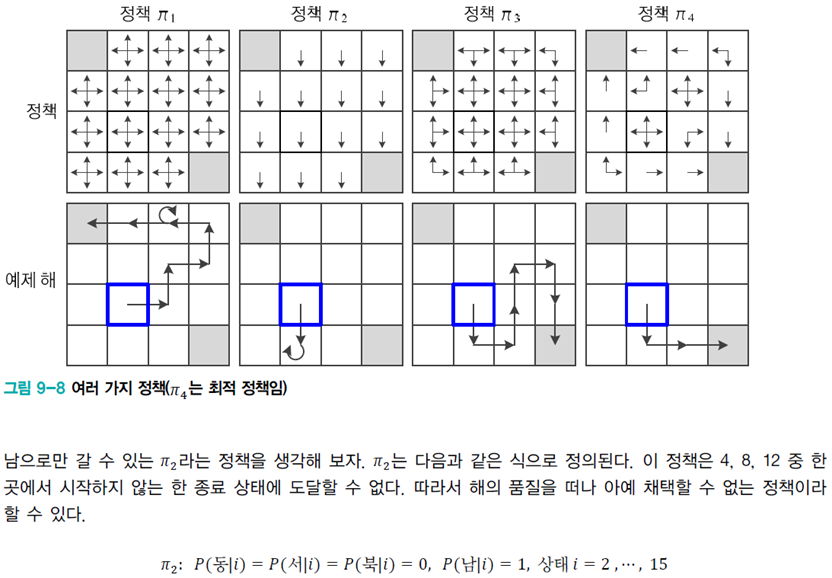


해당 이미지의 내용을 읽어보면 이해하는데 도움이 될 겁니다!
강화학습의 알고리즘이 할 일은

but, policy space가 방대하여 모든 policy를 일일이 평가하고 그중 제일 좋은 것을 선택하는 방법은 현실성이 없다. 따라서 value function을 이용하는 전략을 사용한다.
policy space란 서로 다른 policy의 집합을 말하며, state space보다 훨씬 더 방대하다. 강화학습에서는 직접 exploration하는 것 대신에 value function을 사용한다.
2. value function
value function은 특정 policy의 좋은 정도를 평가하는 함수이다. 특정 polocy에서 모든 state의 좋은 정도를 평가한다.
'좋은 정도'는 state s로부터 종료 상태에 이르기까지의 누적 reward 값의 추정치이다.
value function은 특정 policy 𝜋에서 추정하며 state s의 함수이므로 𝑣_𝜋 (𝑠)라 표기한다.


예제의 내용을 천천히 읽어보십시오!
[예제9-3]을 통해 value function으로 policy를 평가할 수 있음을 알았다.

식으로 쓰면 위와 같고 일반적인 수식으로 다시 표현하면
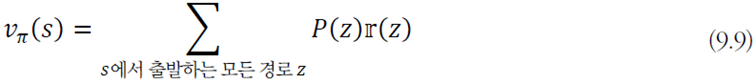
이와 같다. 𝑃(𝑧)는 경로 𝑧의 발생 확률, 𝕣(𝑧)는 경로 𝑧의 누적 reward 값이다.
누적 reward를 계산하는 식은 아래와같다.

1) episodic task
2) continuing task
강화학습에서는 유한한 경로를 가진 과업을 episodic task라고 하며, 무한 경로를 가진 과업을 continuing task라고 한다.
장기나 바둑 같이 일정한 시간이 지나면 반드시 끝나는 경기는 episodic task이고, 제어 시스템처럼 아주 오랜 시간 동작이 지속되는 경우는 continuing task라고 한다.
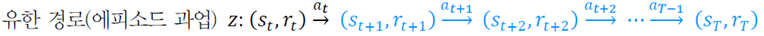
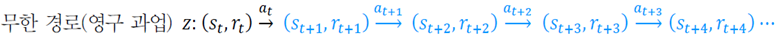
continuing task에서는 reward가 무한대에 가까워질 수 있으므로 reward를 discount한다. 이를 discounted accumulating reward라 하고, 𝛾은 할인율(discount rate)이고 0≤𝛾≤1이다.
이 방법은 현재 state에서 멀어질수록 reward를 discount하여 공헌도를 낮추는 전략이다.
3) Bellman equation
Bellman equation을 만족하는 value function이다. cs231n에서는 이를 Q-value function이라고 한다. 책에는 이 용어가 나오진 않는다.
cs231n의 Lecture14의 slide에는 아래의 내용이 나옵니다.
The optimal Q-value function Q* is the maximum expected cumulative reward achievable from a given (state, action) pair
optimal Q-value function이라는 것은 최적의 Q-value function을 의미하고, (state, action)의 pair을 통해 얻을 수 있는 최대의 누적 reward 값이라고 설명한다.
그리고 Q*이 Ballen equation을 만족한다.
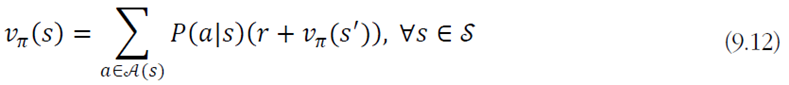
해당 책에서도 수식을 일반화 했을 때 이렇게 바뀐다. 𝑠에서 𝑎를 실행했을 때 𝑠′로 전환되는 과정이다.
여기서는 원래 (𝑠, 𝑎)라고 표기해야 하지만 편의상 𝑠'로 표기하였다.

(cs231n의 강의 슬라이드를 참고하셔서 해당 내용 이해에 도움이 되셨으면 합니다!)
여기서 봐야하는 것은 state 𝑠만 따르던 policy였던 value function이, (𝑠,𝑎)에 따르는 policy로 바뀐 것이 Q-value-function이고, 이것이 결국 optimal policy를 찾는 solution이 된다는 점이다!
그러면 만족한다고 하는 Bellman equation은 도대체 뭘까?

해당 PPT를 보았을 때, Bellman equation을 따른다는 아래의 식을 앞의 식과 비교를 해보자면,
value function은 앞의 state 𝑠를 고려하지 않았지만, agent는 각 state에서 policy에 따른 action을 취해야 하므로, 이를 고려한 value function으로 변환하여야 한다.
이렇게 변환된 policy를 고려한 value function이 Bellman Expectation Equation이다. (해당 식에서 E 기댓값을 사용했음을 알 수 있다.)
즉, Bellman Expectation Equation은 현재 state의 value function과 next state(𝑠')의 value function 사이의 Equation이다.
Bellman equation을 만족하는 수식은 현재 state의 value와 next state의 value 관계를 간결하게 표현하는 식이다.
- state에 대한 함수: value function
- state, action에 대한 함수: Q-value function
그래서 Q-value function은 Bellman equation이라 하는 것이다.
4) Bellman Optimality equation
optimal policy를 찾는 식을 value function으로 다시 표현하면 아래와 같다!
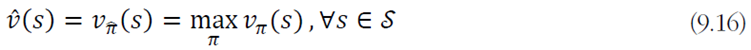
계산 가능한 수식으로 바꾸어 쓰면
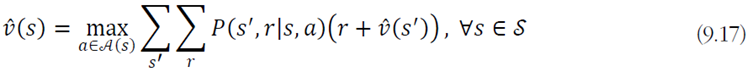
가 된다. 그러면 이제 cs231n에서 던져주는 식을 이해하기에 조금 더 가까워진다.
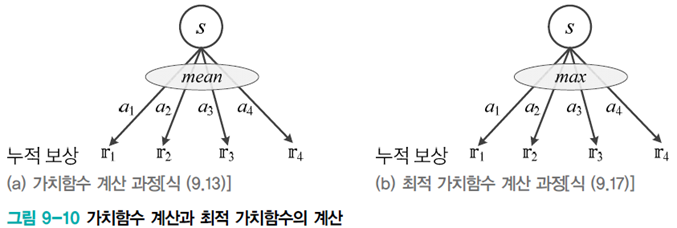
[식9.16]에서 [식9.17]은 mean에서 max로 대치한 것이다. [그림9-10]을 통해 계산 과정을 비교할 수 있다.
이 식을 다시 continuing task로 바꿔쓰면
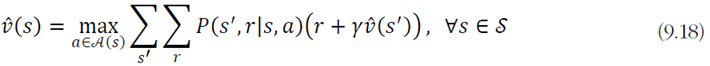
이와 같다.
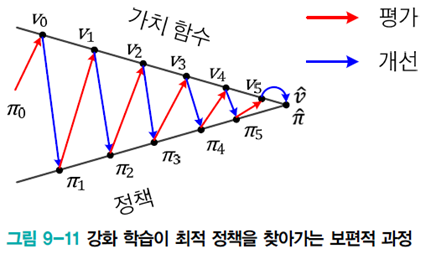
식을 계산 하는 방법은 state들이 순환적으로 연결되어 있는데, 어느 상태도 값이 정해져 있지 않다.
이들을 푸는 보편적 방법으로는
- policy를 임의로 설정하고 출발
- value function 계산
- policy 개선
- value function 계산
…
이를 해결하는 방법은 책에서 여러 가지를 제안하고 있지만, 일단 cs231n 강의 내용을 바탕으로 다시 정리하려고 한다.
