자료 출처
시계열 데이터를 공부할 예정입니다. 저는 'Forecasting: Principles and Practice'이란 온라인으로 올라온 교재 자료를 보고 정리하였습니다.
시계열 시리즈
목차
- 자기 회귀(AR, Autoregressive)
- 이동 평균(Moving Average)
- ARIMA 모델
이동 평균은 고전적인 시계열 분해 기법이라고 합니다.😁 이동 평균은 추세-주기를 측정하기 위해 사용한다고 합니다.
자기 회귀(Autoregressive)
자기 회귀는 무엇일까요? (방금 잠깐 정신줄을 놓다가 자귀 회귀라고 적어 버렸습니다☺)
자기 회귀 모델은 변수의 과거 값의 선형 조합을 이용하여 관심 있는 변수를 예측 하는 방법을 말합니다.
말 그대로 본인을 회귀한다는 의미에서 자기 회귀라고 이름을 지은 것 같습니다. 자신에 대한 변수의 회귀라는 의미가 담겨져 있는 것이죠!
따라서, 차수 p의 자기회귀 모델은 다음과 같이 쓸 수 있습니다.
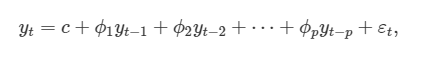
여기에서 εt는 백색잡음(white noise)입니다. 이것을 p 자기회귀 모델인 AR(p) 모델이라고 부릅니다!
자기회귀 모델(autoregressive model)은 다양한 종류의 서로 다른 시계열 패턴을 매우 유연하게 다룰 수 있다고 합니다.
매개변수를 바꾸었을 때 어떤 시계열 패턴이 나오는지 그림으로 보겠습니다.
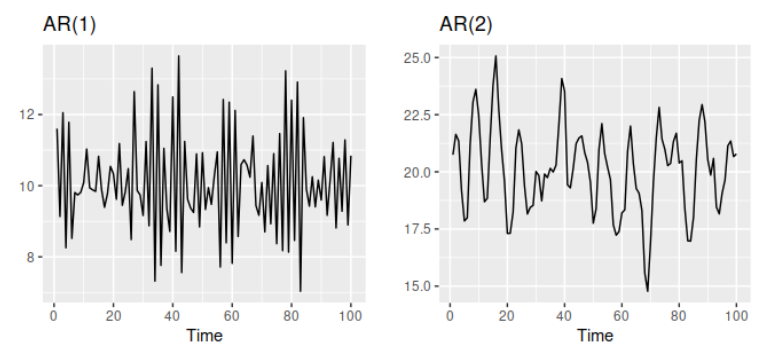
Figure: 매개변수를 다르게 설정한 자기회귀 모델로부터 얻은 데이터의 두 가지 예
이동 평균(moving average)
차수 m의 이동 평균의 식은 아래와 같습니다.
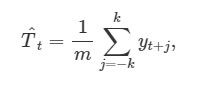
m = 2k+1 입니다 즉, k 기간 안의 시계열 값을 평균하여 t의 추세-주기를 측정하는 것입니다.
측정 시기가 비슷하면 값도 비슷해집니다. 따라서 평균이 데이터의 무작위성을 줄여주며 매끄러운 추세-주기 성분만 남긴다고 합니다.
Table: 남 호주 지역 연간 주거용 전력 판매량. 1989–2008.
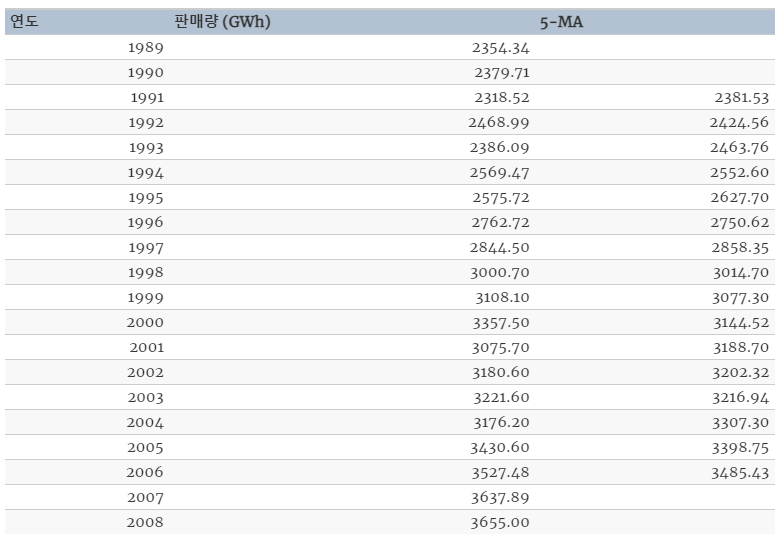
위의 table을 보면 추세-주기(trend-cycle)의 측정값을 나타내는 차수(order) 5의 이동 평균(moving average)가 있습니다.
차수가 5이니 1989–1993, 1990–1994, 1991-1995, ... 순으로 계산한 평균이 적혀 있는 것입니다. 5년이 각 기간이 되는 것입니다.
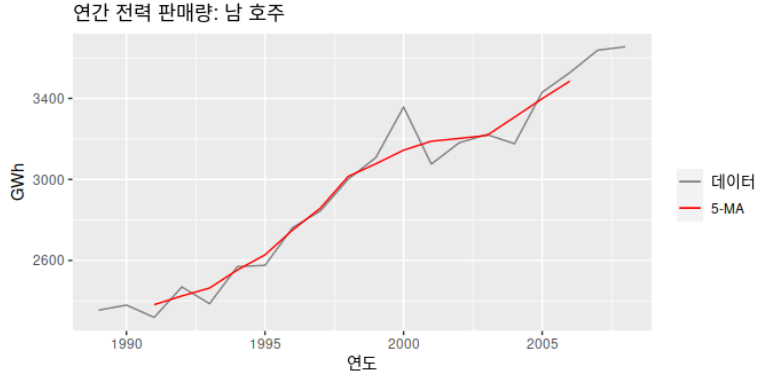
원래의 데이터에서 5-MA가 더 매끄럽다는 것을 알 수 있죠?
이동평균(moving average)의 차수(order)는 추세-주기 추정치의 매끄러운 정도를 결정합니다. 일반적으로, 더 큰 차수가 더 매끄러운 곡선을 의미합니다.
지금까지 MA, 이동 평균을 아주 간단하게 살펴보았습니다!
ARIMA 모델
ARIMA 모델은 시계열을 예측하는 또 하나의 접근 방법입니다. ARIMA 모델은 시계열을 예측할 때 가장 널리 사용하는 접근 방식이고, 주어진 문제를 상호 보완적으로 다루도록 하는 접근 방식입니다.
ARIMA 모델은 데이터에 나타나는 자기상관(autocorrelation)을 표현하는데 목적이 있습니다.
차분을 구하는 것을 자기회귀와 이동 평균 모델과 결합하면, 비-계절성(non-seasonal) ARIMA 모델을 얻을 수 있습니다.
ARIMA는 AutoRegressive Integrated Moving Average (이동 평균을 누적한 자기회귀)의 약자입니다. 이 맥락에서 “누적(integration)”은 차분의 반대 의미를 갖습니다).
자기회귀(autoregression)와 이동 평균 모델에 사용되는 것과 같은 정상성(stationarity)과 가역성(invertiblity) 조건은 ARIMA 모델에도 적용됩니다.
ARIMA 모델의 모수 p, q, d
ARIMA를 효과적으로 활용하기 위해서는 ARIMA의 모수(parameter)를 잘 설정해야 합니다.
이 파라미터가 올바른 예측식을 구하는데 핵심적인 요소가 됩니다.
- p : 자기회귀 모형(AR)의 시차
- q : 이동평균 모형(MA)의 시차
- d : 차분누적(I) 횟수
p와 q는 일반적으로 p + q < 2, p * q=0인 값을 사용한다고 합니다. p와 q 중 하나는 0이라는 뜻인데, 시계열 데이터가 AR이나 MA 중 하나의 경향만 가지기 때문입니다.
ACF, PACF
개념 정리 자료 출처: 여기
이제 모수를 설정하는데 중요한 ACF, PACF를 설명하고 있습니다.
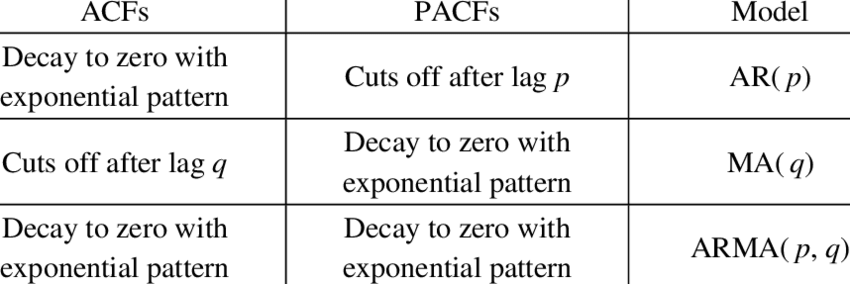
이미지 출처: The model identification from ACF and PACF plots Download Table (researchgate.net)
ACF를 통해 MA 모델의 시차 q를 결정하고, PACF를 통해 AR 모델의 시차 p를 결정할 수 있습니다.
자기상관함수(Autocorrelation Fucntion, ACF)
ACF는 yt와 yt+k 사이에 correlation을 측정하는 것입니다. yt와 yt+k가 얼마나 관계가 있는지를 측정하는 것이며, 수식은 아래와 같습니다.
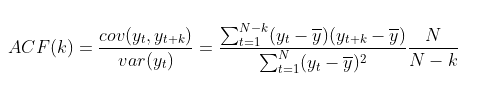
yt와 yt+k의 공분산에 yt의 분산을 나누어주었습니다.
이처럼 수식에서 확인할 수 잇듯이, k가 값이 커짐에 따라 ACF(k)의 값은 작아집니다.
ACF의 주요 성질로는
- ACF(0) = 1
- ACF(k) = ACK(-k)
입니다!
편자기상관함수(Partial Autocorrelation Fucntion, PACF)
ACF는 분명히 활용성이 뛰어나고 중요한 Tool이지만 모든 시계열 데이터의 특성을 분석하는 것에는 한계가 있습니다.
시계열 모델 중에 대표적인 AR(q)모델이나 MA(p)모델중에 어떤 것을 활용하고 어떤 시차(lag)를 적용할지에 대해서 ACF만을 활용하여 결정하는 것은 어렵습니다.
그렇기 때문에 PACF를 활용한 추가적인 분석이 필요합니다.
PACF는 yt와 yt+k와의 correlation을 측정하는 것은 ACF와 동일하나, t와 t+k 사이에 다른 y값들의 영향력을 배제하고 측정합니다.
수식은 다음과 같습니다.
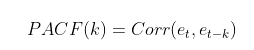
이 식에서 et는
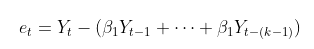
를 의미합니다.
즉, et는 yt−k를 제외하고 yt−1에서 yt−(k−1)로 설명될 부분들을 제거한 것입니다. et−k도 마찬가지로 볼 수 있습니다.
따라서 Corr(et,et−1)을 계산한다는 것은 온전히 yt와 yt+k의 관계만 보는 것입니다.
AR, MA 모델을 결정할 때, ACF와 PACF는 데이터 상황에 따라 다르지만
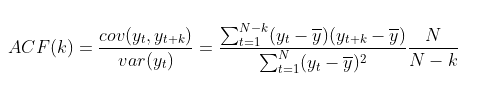
이렇게 활용될 수 있습니다!

