시계열 패턴(trend, seasonality, cycle), 잔차(Residual)

미남로그·2021년 9월 3일

시계열 데이터를 공부할 예정입니다. 저는 'Forecasting: Principles and Practice'이란 온라인으로 올라온 교재 자료를 보고 정리하였습니다.

1. 시계열 패턴

시계열을 이해하고 왔다면, 더 잘 이해하기 위해 추세(trend)와 계절성(seasonality) 같은 단어를 정의하면 좋습니다.

데이터가 장기적으로 증가하거나 감소할 때, 추세(trend)가 존재합니다. 추세는 선형적일 필요가 없다고 합니다. 때때로 어떤 추세가 증가에서 감소로 변화하는 경우에, 그것을 '추세의 방향이 변화했다'라고 말할 수 있습니다.

해마다, 특정한 때, 1주일마다, 특정 요일마다 나타나는 것 같은 계절성 요일이 시계열에 영향을 줄 때, 계절성(seasonality) 패턴이 나타납니다.

계절성은 '빈도'의 형태로 나타납니다. 빈도가 항상 일정하며 알려져 있어야 합니다.

고정된 빈두가 아닌 형태로 증가나 감소하는 모습을 보일 때 주기(cycle)이 나타납니다. 보통 이러한 변동은 경제 상황 때문에 나타난다고 합니다.

막상 이렇게 3개를 정리하고 보니 저도 주기성과 계절성이 헷갈립니다.🙄 하지만 이 둘은 아주아주아주 다르다고 하네요.

일정한 빈도로 나타나지 않는 요동은 주기적입니다. 빈도가 변하지 않고 연중 어떤 시기와 관련되어 있는 것이 계절성입니다.

예를 들어, '타이레놀 월별 매출액'으로 비유를 들자면 월별 매출액에는 월별이라는 빈도의 형태가있고, 일정합니다. 연말에 매출이 조금 더 오르는데 이건 계절성이 나타난다고 볼 수 있습니다. 연중 어떤 특정한 시기와 연관되어 있기 때문입니다.

하지만 코로나 때문에 '타이레놀'은 많이 팔렸습니다. 매출이 급격히 뛰었습니다. 이는 계절성 패턴의 길이보다 길고 변동성이 더 큽니다. 이는 일정한 빈도로 나타나지 않기도 합니다. 이를 주기성이라고 합니다.

많은 시계열 데이터에는 추세(trend), 계절성(seasonality), 주기(cycle)가 있습니다.

시계열 모델에서 “잔차(Residuals)”는 모델을 맞춘 후에 남는 것을 의미합니다.

다양한 시계열 모델에서, 잔차(residual) 는 관측값과 대응되는 적합값(fitted value)과 관측값의 차이와 같습니다.

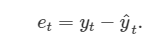
노드에서는 시계열 분해 개념에서 잔차(residual)의 개념이 등장합니다. 시계열 안에 추세(trend)와 계절성(seasonal)이 있는 경우, 이동 평균 제거, 차분(differencing) 등을 거치지 않고 정상성 시계열을 분리할 수 있는 방법을 제시하는데요.

그것이 시계열에서 추세(trend)와 계절성(seasonal)을 제거하고 난 나머지, 잔차(Residual)를 통해 p-value 값을 구하는 방법이었습니다.

잔차(residual)는 어떤 모델이 데이터의 정보를 적절하게 잡아냈는지 여부를 확인할 때 유용합니다. 좋은 예측 기법은 다음과 같은 특징을 갖는 잔차(residual)를 냅니다.

잔차(residual)에는 상관 관계가 없습니다. 잔차 사이에 상관관계(correlation)가 있다면, 잔차에 예측값을 계산할 때 사용해야하는 정보가 남아 있다는 것을 의미합니다.

미남이 귀엽죠