12강 바로 보러가기 클릭
이상하게 12강은 한국어 자막이 없네요. 자막 설정 시, 영어 자막이 뜹니다. 오늘은 크래머 공식의 기하학적 의미에 대한 강의입니다.
이 12강을 공부하기 전에, 아래의 3개의 강의를 보고 오면 좋다고 합니다.
행렬식과 내적과 이중성, 역행렬과 Rank, Null space에 대한 이해를 필요로 하고 있습니다.
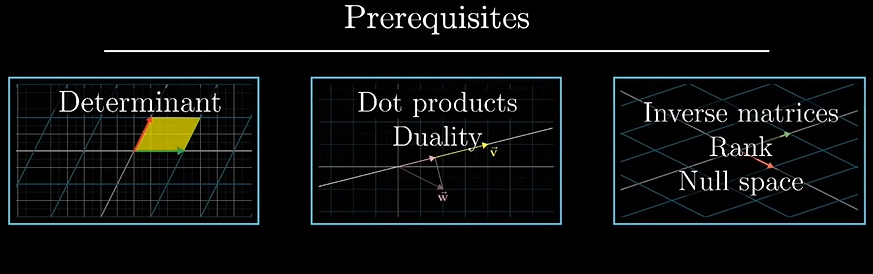
행렬식의 이해
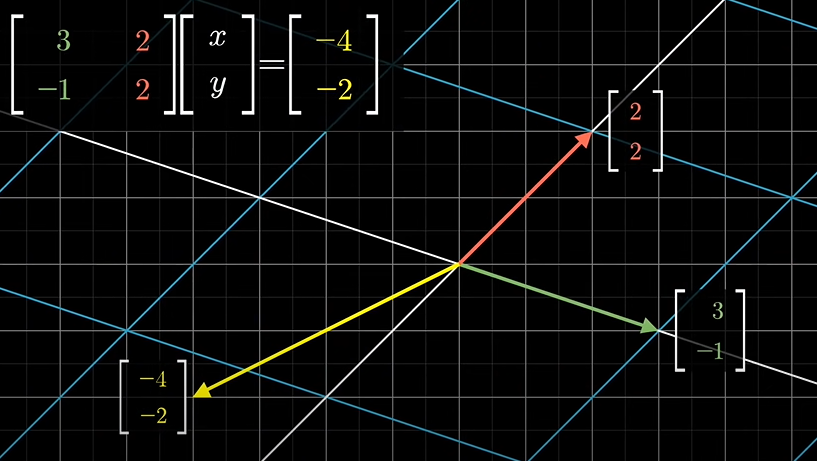
위의 행렬식을 통해서 두 기저 벡터에 의한 변환을 알 수 있습니다.
또한, 각 열벡터로 구성된 평행사변형의 넓이와 같은 의미를 갖는다는 것을 앞에서 배웠습니다.
0의 행렬식
det(A)=0인 0의 행렬식은 무엇을 의미하나요? 입력 중 어느 것도 주어진 출력에 도달하지 않거나 해당 출력에 도달하는 입력이 있습니다.
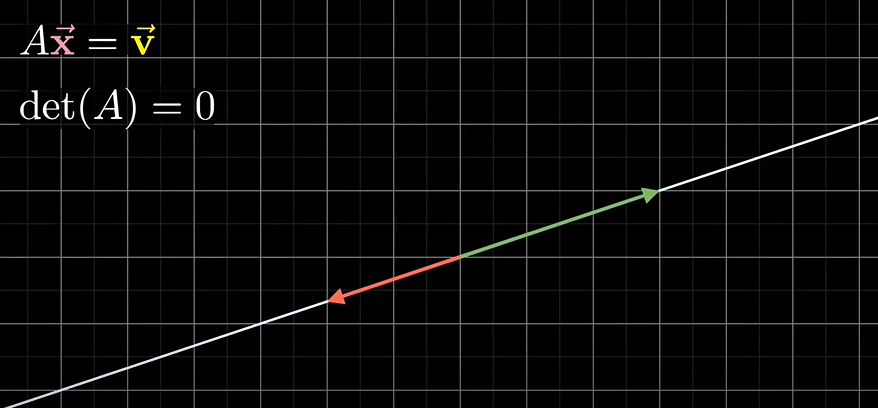
이건 입력의 차원의 축소를 생각하면 더 쉬운데요. 평생사변형을 구성하는 벡터가 평행이면 이 넓이는 무조건 0이 됩니다.
용어를 사용하여 표현하면,
행렬 A의 열벡터가 모두 선형독립이 아니라면 평생사변형의 넓이는 0이 되고, 역행렬을 갖지 않는 행렬이 됩니다.
0의 행렬식이 아니라 전제
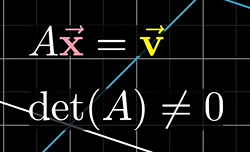
이 비디오에서는 행렬식이 0이 아니라고 전제한다고 합니다.
크래머 공식
평행사변형의 넓이를 구하는 방법은 어떻게 되나요?
평행사변형의 넓이 = 밑변 x 높이
생각보다 간단합니다!
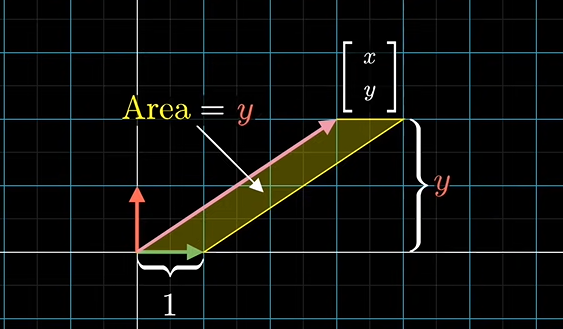
위 이미지에서 Area는 벡터의 y좌표를 설명하는 값이 됩니다.
크래머 공식의 기하학적 의미는 행렬식이 결국 두 벡터가 이루는 평행사변형의 넓이와 같다는 점과 밑변 x 높이로 계산할 수 있다는 두 가지 사실이 기하학적 의미를 해석할 수 있습니다.
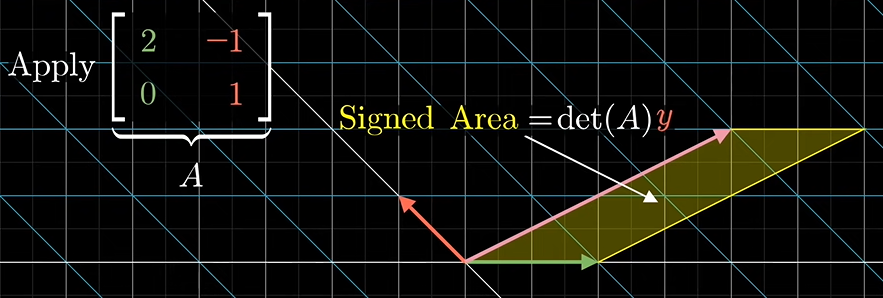
여기서 평행사변형의 넓이가 저렇게 표현이 되었듯이 y좌표는

해당 식으로 표현될 수 있습니다.
평행사변형의 넓이에 행렬식을 나눈 값입니다.
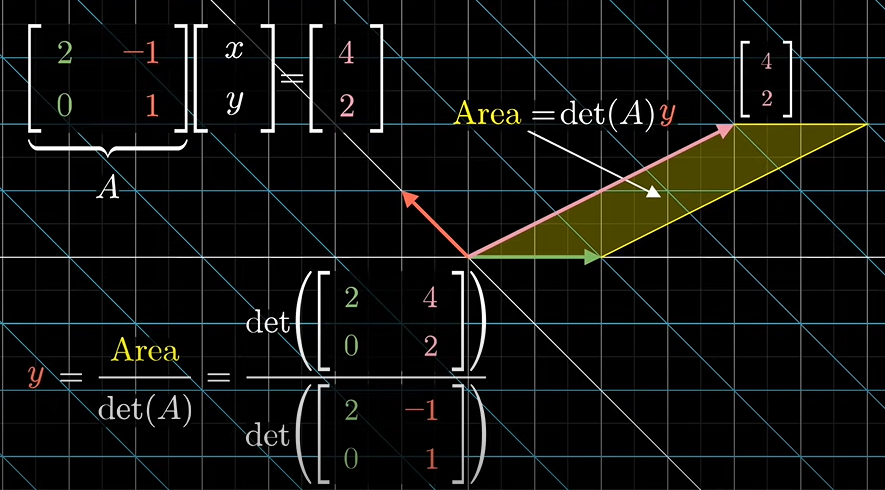
위 사진을 통해서 y가 어떻게 구해지는지 이해가 가실 것입니다!
y를 구하기 위해 첫 번째 열에 행렬의 첫 번째 벡터가 오고 두 번째 열에 출력되는 벡터 값이 옵니다.
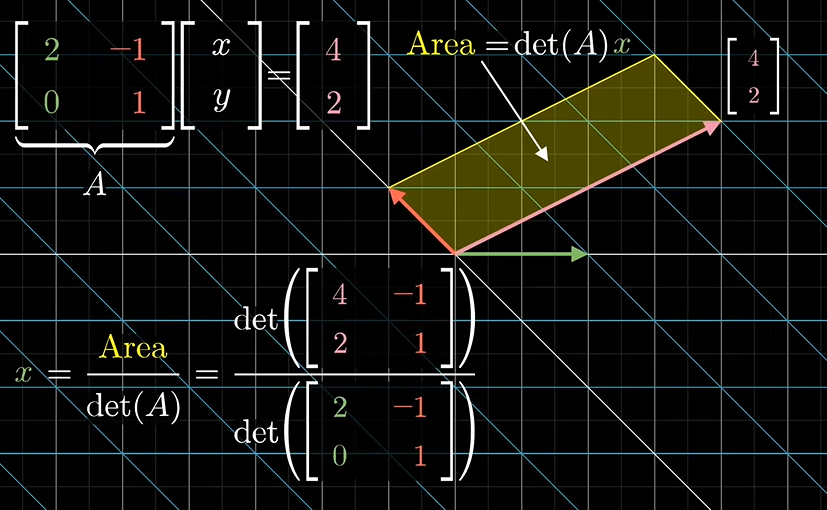
x를 구할 때도 방식은 같습니다. 첫 번째 열이 출력 벡터가 되고 두 번째 열이 행렬의 두 번째 벡터 자리에 옵니다.
이런식으로 선형 시스템에서 볼 수 있는 숫자인 벡터 값을 이용하여 해를 구하는 방식을 크래머 공식이라 합니다.
선형 방정식의 연립을 이용한 방법입니다.
즉, 크래머 공식은 방정식의 해를 얻을 때 사용할 수 있는 공식입니다.
임의의 nxn 사이즈 행렬 A와 nx1 사이즈의 벡터 b, x=[x_1, x_2, ..., x_n].T 가 있다면,
Ax=b
가 성립할 때, 솔루션 x의 각 원소 x_i for 1,2,...,n은
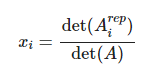
와 같이 정해진다는 공식입니다.
여기서 A_i(rep)는 행렬 A의 i번째 열을 b벡터로 치환한 행렬입니다.
크래머 공식을 더 자세히 이해하고 싶다면 해당 블로그를 추천합니다.
공돌이의 수학노트: 크래머 공식의 기하학적 의미
