Linear Algebra

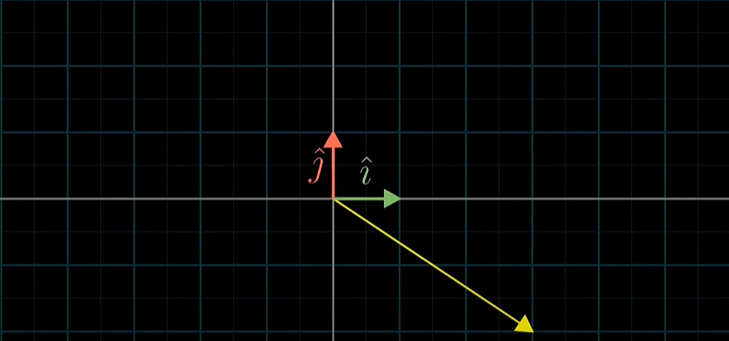
오른쪽 방향의 길이 1벡터를 "아이-햇(i-hat)"이라 부르며, x축의 단위벡터라고 합니다.위쪽 방향으로 길이 1벡터를 "제이-햇(j-hat)"이라 부르거나 y축의 단위벡터라고 합니다.이 둘을 좌표계의 기저(basis)라고 부릅니다. 기저(basis) 벡터들은 그 스

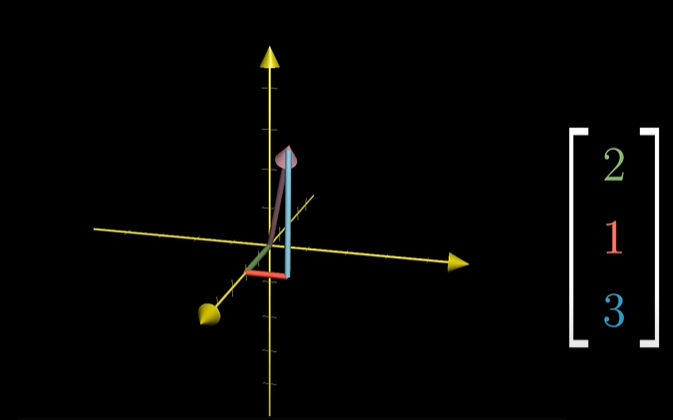
1강 Vector 강의벡터의 합벡터의 곱선형대수의 벡터는 원점에 뿌리를 둔다.숫자 리스트는 벡터의 좌표를 의미 리스트 형태로 벡터를 두는 건 기하학적 해석이다. ex. -2, 3 모든 숫자쌍은 각각 하나의 벡터와 대응되고 반대로 모든 벡터는 각각 대응되는 숫자쌍이

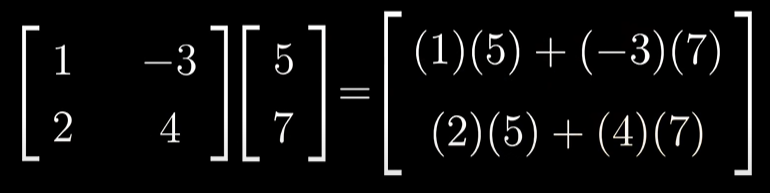
"불행히도, 아무도 매트릭스가 무엇인지 말할 수 없으니 직접 봐야합니다."영화, 매트릭스 모피어스다들 영화 매트릭스 보셨나요? Matrix가 무엇일까요?😁선형변환입력을 받고 결과물을 반환하는 무엇특정 벡터를 다른 벡터로 바꾸는 변환 같은 것입니다."함수(functio

기저 벡터가 선형 변환에 의해 어떻게 옮겨졌는지를 알면 그 선형 변환이 무엇인지 파악할 수 있습니다.예를 들어, 2차원 공간에서는 i-hat, j-hat으로 말입니다. 모든 벡터들은 i-hat, j-hat의 선형 결합으로 모두 표현이 가능하기 때문입니다.선형 변환 이후

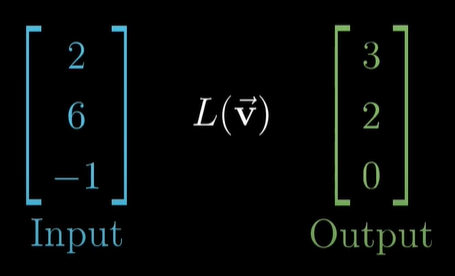
3차원 벡터를 입력 받아서 3차원 벡터를 출력합니다.3차원 공간을 상상해 봅시다. 2차원 공간과 같이 격자선은 평행하고, 간격이 일정합니다. 원점은 고정되어 있습니다. 공간의 모든 점들은 벡터의 끝점을 대신합니다. 입력(input) 벡터를 받아서 움직여서 대엉되는 결과

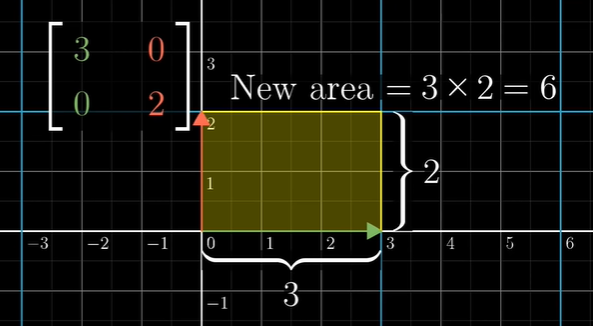
6강 강의 바로가기예전에 선형대수학 수업을 들었을 때, 행렬식에 대해 배웠었다. 행렬식(determinants)이란 역의 존재 \- 역수의 존재(ab=1을 만족하는 실수 a의 역수 b가 존재할 조건은 a != 0 일 때)역 행렬의 존재(AB=I을 만족하는 행렬 A의

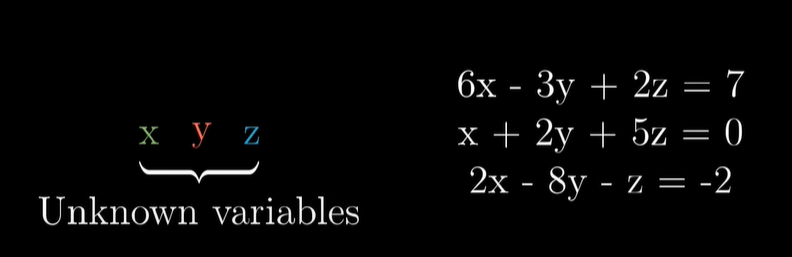
강의 보기System of equationsInverse matricesRankColumn spaceNull space방정식계란 미지수인 변수 리스트와 변수들과 관련된 방정식의 리스트를 가진 경우를 말합니다.각 방정식 내에서 각 변수들의 역할은 어떤 상수를 스케일링하는

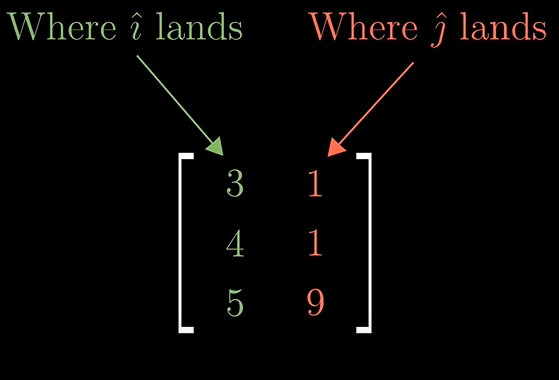
Chapter8 강의 보기이번 강의는 이때까지 배웠던 행렬식(determinant)과는 다른 형태를 배우게 될 것입니다. 왜냐하면 이때까지 2x2, 3x3 같은 n차 정방 행렬만 보았기 때문입니다!그래서 저희는 선형변환도 2→2차원, 3→3차원의 변형만 다루었죠.오늘은

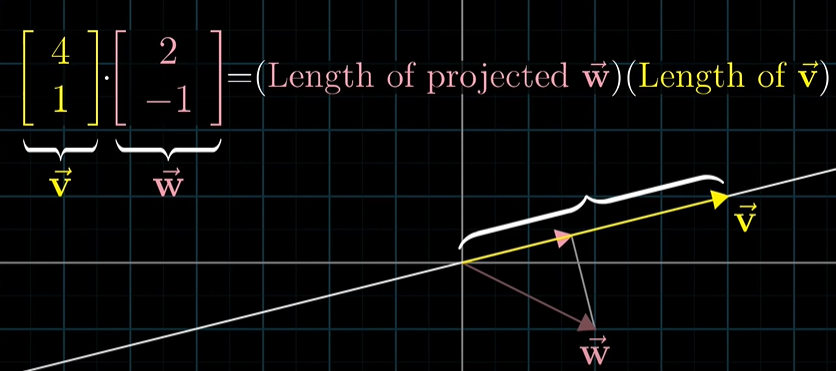
강의 바로 보러 가기 클릭보통 내적의 개념은 선형대수학에서 벡터를 배우고 난 바로 뒤에 위치해 있습니다. 하지만 이 강의에서는 챕터 9에서야 내적에 대한 개념을 보여주고 있습니다. 내적에 대한 이해가 뒤에서 하는 것이 더 쉽다고 하는데요! 내적이 무엇인지 알아보러 갑시

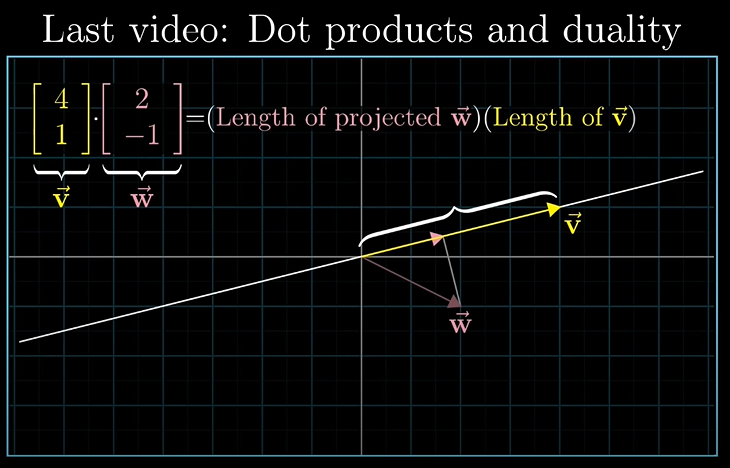
강의 보러가기: 클릭지난 강의에서는 내적(dot product)과 선형 변환에 대해 배웠습니다.이번 강의에서는 외적(cross product)에 대해 설명할 예정입니다.벡터 v, w의 외적은 x 기호를 사용하여 v X w 라고 적고, 평행사변형의 면적(area)를 뜻합

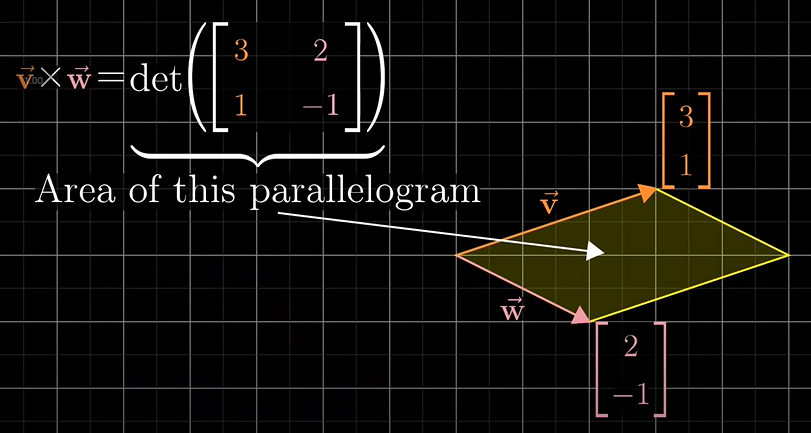
강의 보러 가기 ch11. Cross products Chapter 11 Cross products in the light of linear transformations 이번 챕터 11을 공부하기 위해서 선행 학습이 되어야 하는 부분이 있습니다. 바로 행렬식을

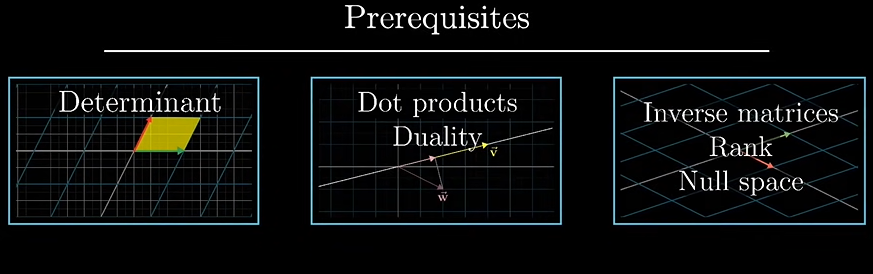
12강 바로 보러가기 클릭이상하게 12강은 한국어 자막이 없네요. 자막 설정 시, 영어 자막이 뜹니다. 오늘은 크래머 공식의 기하학적 의미에 대한 강의입니다.이 12강을 공부하기 전에, 아래의 3개의 강의를 보고 오면 좋다고 합니다.행렬식과 내적과 이중성, 역행렬과 R