자료 출처

시계열 데이터를 공부할 예정입니다. 저는 'Forecasting: Principles and Practice'이란 온라인으로 올라온 교재 자료를 보고 정리하였습니다.

FPP

시계열 시리즈

1. 시계열 데이터 정리
2. 관련 통계 개념 정리
3. 시계열 패턴과 잔차
4. 자기 회귀(Autoregressive), 이동 평균(Moving average), ARIMA 모델

목차

시계열 데이터를 다루기 전에 통계학에서 나오는 개념을 공부하고 가려고 합니다!

지금 포스팅에서 정리할 것은

1. 평균(average)
2. 분산(Variance)
3. 공분산(Covariance)
4. 상관계수(Correlation)
5. 자기공분산(Autocovariance)
6. 자기상관계수(Autocorrelation)
7. Q&A
8. 정리

입니다! (와 차라리 죽여줘🥺)

정상성 시계열

아까 정상성을 갖는 시계열 데이터를 공부하고 왔습니다.(보러 가기) 정상성(stationarity)을 나타내는 시계열은 시계열의 특징이 해당 시계열이 관측된 시간에 무관해야 합니다. 또한, 이 시간의 추이와 상관없이 일정해야 하는 통계적인 특성이 세 가지 있습니다.

1. 평균
2. 분산
3. 자기공분산

입니다.

이 말은 다시 설명하면 시계열의 평균과 분산, 자기공분산이 시간의 흐름에 따라 체계적으로 변화하지 않아야 한다는 것입니다. 만약 이것이 정상성이 아닐 경우엔 문제가 될 수 있습니다.

평균(average)

자료 집합의 평균값은 자료 집합내의 모든 값을 더하여 자료의 개수로 나눈 것입니다.

이것은 확률론에서는 기댓값이라고도 말합니다. 어떤 확률적 사건에 대한 평균의 의미입니다. 모평균이라고도 합니다.

통계학에서는 평균말고 표본 평균이라는 개념도 있는데요. 표본 평균이란 것은 모집단에서 표본을 추출하여 그 표본들의 평균을 구하고 그 평균의 집단을 대표하는 값을 말합니다.

분산(Variance)

분산(variance)은 관측값에서 평균을 뺀 값을 제곱하여 모두 더한 값에 전체 개수로 나눠서 구한 값을 말합니다. 즉, 차이값의 제곱의 평균이다.

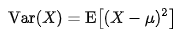
공분산(Covariance)

2개의 확률변수의 선형 관계를 나타내는 값입니다. 만약 2개의 변수가 있는데 하나의 값이 상승하는 경향을 보일 때, 다른 값도 상승하는 선형 상관성이 있다면 양수의 공분산을 가진다고 말할 수 있습니다.

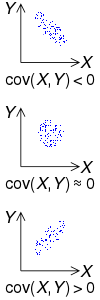
두 개의 확률 변수 X, Y의 상관성과 공분산의 부호입니다.

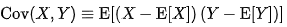
공식은 이렇습니다!

공분산은 확률변수들의 벡터 공간 상에서의 내적을 의미하기도 합니다. 벡터에서 적용되는 벡터합 X + Y 및 aX와 같은 스칼라곱의 성질도 지닙니다.

상관계수(Correlation)

상관 계수는 상관관계 분석에서 두 변수 간에 선형 관계의 정도를 수량화하는 측도룰 말합니다.

두 변수 X, Y 사이의 상관관계 정도를 나타내는 수치를 말하는 것이죠! 상관계수는 피어슨(Karl Pearson)에 의해 제안되었기 때문에 피어슨의 상관계수라고도 합니다.

보통 기호는 r로 표시하며 -1부터 1까지의 값을 가집니다. 절댓값의 크기로 생각하고 1에 가까울 수록 두 변수 간의 연관성이 크고, 0에 가까울 수록 매우 약함을 의미한다고 생각하면 됩니다.

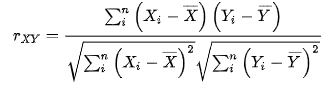
식은 이렇습니다.

상관계수 = 공분산 / 표준편차 * 표준편차 입니다.

자기공분산(Autocovariance)

공분산은 동일한 시간에서 2개 변수의 상관관계를 분석하는 것을 의미하는데요. 그렇다면 자기 공분산은 무엇일까요?

자기공분산은 서로 다른 2개의 시간에 대한 변수 값의 공분산을 계산하는 것입니다. 그렇기 때문에 시계열 데이터에서 시간의 추이와 상관없이 일정해야하는 것이 공분산이 아닌 '자기공분산'이었던 것이죠.

자기공분산 함수는 시간에 따른 값들의 상관 관계가 어떻게 되는지 파악할 수 있습니다. 따라서 자기공분산 함수는 시계열 데이터의 추세와 크기를 파악하는 데에 용이하게 활용됩니다.

자기상관계수(Autocorrelation)

공분산과 자기공분산의 차이처럼, 상관계수와 자기상관계수의 차이도 비슷합니다.

상관계수는 특정 동일 시점을 횡단면으로 해서 Y와 다른 X1, X2, ... 변수들 간의 관계를 분석하는 것입니다.

자기상관계수는 동일한 변수(Yt, Yt-1, Yt-2, ...)의 서로 다른 시간 차이(time lag)를 두고 관계를 분석하는 것입니다.

즉, 상관계수가 두 변수 사이의 선형 관계의 크기를 측정하는 것처럼, 자기상관계수는 시계열의 시차 값 사이의 선형 관계를 측정합니다.

시차 그래프가 있다면 각 패널과 몇 가지 자기상관 계수가 있습니다.

예를 들어, r1은 yt와 yt-1 사이의 관계를 측정하고, r2는 yt와 yt-2 사이의 관계를 측정하는 식입니다!

rk를 식으로 표현하면,

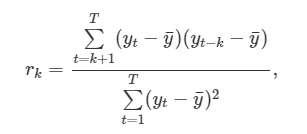
이렇습니다!

여기서 T는 시계열의 길이를 뜻합니다.

아래의 표는 맥주 생산량 데이터에 대한 처음 9개의 자기상관계수를 의미합니다.

• r4는 다른 시차들보다 값이 높습니다. 이것은 계절성 패턴 때문입니다.
• r2는 다른 시차들보다 더 큰 음의 값을 가집니다. 저점이 고점 직후의 2개 분기마다 나타나는 경향이 있기 때문입니다.

이렇게 간단히 개념 용어를 정리해보았습니다.

Q&A

1. 공분산(Covariance)와 상관계수(Correlation)의 차이?

공분산이 0보다 크면 X가 증가할 때 Y도 증가한다는 것을 의미하고, 0보다 작으면 X가 증가할 때 Y는 감소합니다. 만약 공분산이 0이면 두 변수 간에는 아무런 상관 관계가 없다고 말합니다.

이렇게 공분산은 두 변수 간에 양의 상관관계가 있는지, 음의 상관관계가 있는지를 알려줍니다. 하지만 상관관계가 얼마나 큰 지는 알 수 없습니다!

그것을 알려주기 위한 것이 상관계수입니다. 위로 올라가서 식을 보고 오면 더 이해가 빠를 것입니다. 왜냐하면 공분산에 각각의 표준편차의 곱을 나누어주었기 때문인데요.

r은 [-1, 1]의 값을 가진다고 하였죠. 이것은 양과 음의 상관관계를 알려줄 뿐만 아니라, r의 절댓값이 1에 가깝냐에 따라 얼마나 상관성이 큰 지를 알 수 있습니다.

• 1에 가까울 수록 상관성이 큰 것(절댓값 기준)
• 0에 가까울 수록 상관성이 작은 것

2. 만약 변수 X와 X의 상관계수를 구한다면?

그것은 분산을 뜻합니다. 분산으로서 데이터의 분포를 알 수 있기 때문이죠. 그래서 X와 X의 상관계수는 분산 그 자체입니다!

3. 두 확률변수 X, Y가 서로 독립이면 공분산(Covariance)와 상관계수(Correlation)은 어떻게 되나요?

독립이라는 조건은 두 변수의 모든 관계가 없다는 것을 의미합니다. 그렇다면 공분산은 두 확률변수 간에 상관관계를 알려주는 것이기 때문에 서로 독립이면 모든 관계가 없다는 것을 의미하기 때문에 공분산은 0입니다.

근데 상관계수는 얼마일까요? 상관계수는 공분산에 각각 변수의 표준편차의 곱을 나눠주는 식이었습니다. 그래서 상관계수도 단순하게 0이 된다고 이해하면 됩니다. 서로 간의 상관관계가 없기 때문에 상관성을 알려주는 상관계수도 0을 의미합니다.

4. 자기와의 공분산이라면 그냥 분산이 되는데, 분산이라고 하지 않고 자기공분산이라고 하는 이유는 무엇인가요?

공분산과 자기공분산의 차이에는 시간에 대한 변수 차이가 있었습니다. 즉, 자기공분산이란 일정 시간 h를 사이에 둔 자기자신과의 공분산을 의미합니다.

5. X(t)와 X(t+h) 사이의 공분산과 X(t-h)와 X(t) 사이의 공분산은 항상 일정한가요? 아니면 어떤 조건 하에서만 성립하나요?

X가 만약 정상성 시계열 변수라면 두 식 사이의 공분산은 일정합니다. 정상성 시계열에 한해 시차가 같다면 데이터의 상관성이 동일한 주기성을 보여줍니다.

정리

지금까지 통계적 용어를 간단하게 정리해보았고, 정상성 시계열은 해당 시계열이 관측된 시간에 무관해야 한다는 점을 살펴보았고, 이에 근거하여 평균과 분산, 자기공분산이 일정해야 한다는 것을 배웠습니다.