Generative model - ①

Learning a Generative Model

input에 대한 distribution $p(x)$ (e.g., 강아지 이미지)를 학습

$p(x)$를 학습해서, 우리는

• Generation : 새로운 강아지 이미지 $\tilde{x}$를 sampling
• Density estimation : 어떤 사진이 $p(x)$에 주어졌을 때, 이 사진이 강아지 같은지 아닌지 판단
  • Density는 Probability의 의미
  • 어떤 이미지가 강아지와 유사하면 값이 크고, 아니면 낮음
  • explicit model이라고 부름
    
    

베르누이 분포(Bernoulli distribution)

• 나올 수 있는 경우의 수는 2개
• parameter는 1개(p)
  
  

Categorical distribution

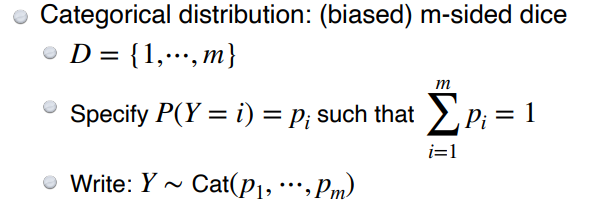
• m개의 면을 갖는 주사위를 던질 때의 확률
• m-1개의 parameter가 필요 (m-1개를 알면 나머지 한 개는 1에서 빼주면 됨)
  
  
  

• 흑백 이미지이므로 0, 1로 표현 가능 → $2^{n}$개의 경우가 존재
• 매우 많은 parameter가 필요
  
  

---

Independence

• 필요한 parameter 수를 상당히 많이 줄여줌
• 각 pixel을 독립적으로 계산했기 때문에, 유의미한 output은 도출하기 어려움
  
  
  
  

---

Conditional Independence

$If\ x⊥y|z, \ then\ p(x|y,\ z) = p(x|z)$

z가 주어졌을 때 x, y가 independent하다면, 조건부 확률에서 y를 제거해도 상관없음

chain rule

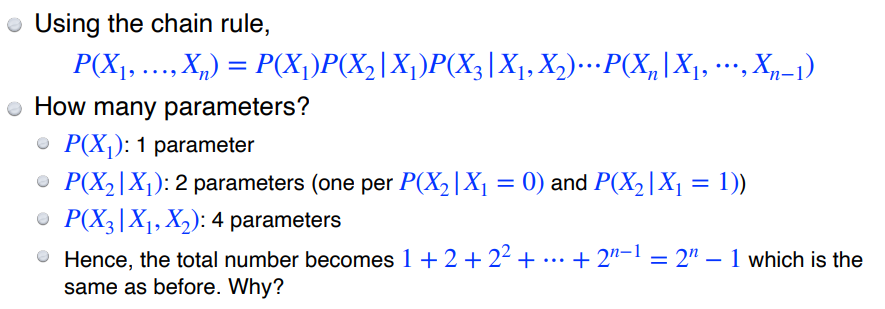
• $P(X_{1})$ = 0 or 1 : P(X)는 pixel에 대한 확률분포로 0 또는 1 값만 가질 수 있음**

• $p(x_{2}|x_{1})$은 $x_{1}$이 0 또는 1의 값을 가질 수 있어 parameter가 2개 필요하며, $p(x_{1})$의 경우 parameter가 1개 필요하므로 총 parameter은 2n-1
  
• 완전 종속 관계일 때에 비해 파라미터 수가 많이 줄어들음

---

Autoregressive Model

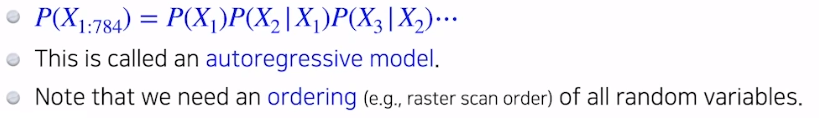
• 임의의 방법으로 2 또는 3차원의 이미지를 한 줄로 피는 ordering 작업이 필요하다.
  • 모든 random variables에 대해 한 줄로 펼침 (784차원 벡터)
• 장점
  • Sampling이 쉬움 (Sequential한 sampling)
  • 병렬화가 불가능해 생성은 느림
  • 새로운 이미지에 대해 probability를 계산할 수 있음
    • 이 때는 병렬화가 가능해 빠름

Nade

• explicit model
• discrete random variable 뿐만 아니라 continuous random variable에 대해서도 modeling 가능
  
  
  
  
  
  
  
  

---

---

※ 모든 이미지의 출처는 네이버 커넥트재단 부스트캠프 AI Tech 5기입니다. ※