Generative model - ②

Maximum Likelihood Learning

어떤 기준으로 분포 사이의 거리가 좋다는 것을 판단할 것인가?

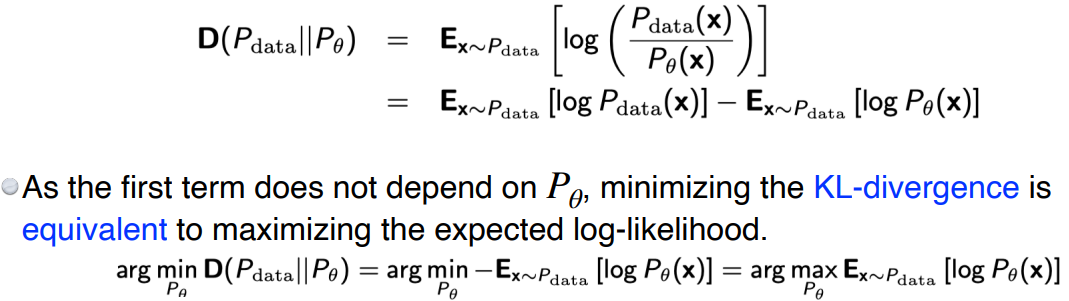
KL-divergence

$P_{data}$ : 실제 강아지 사진의 distribution

$P_{θ}$ : 우리가 모델링해서 얻은 강아지 사진의 distribution

KL-divergence 값을 최소화하는 것이 두 분포의 거리를 최소화하는 것이다.

• 수식에 따라 $logP_{θ}(x)$를 최대화하면, 해당 값은 음수이기 때문에 KL-divergence가 작아진다.
  
  
  
  

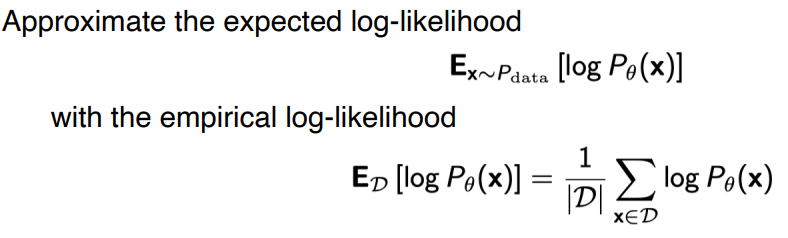
• 전체 data에 대해 기대값을 구하는 것은 불가능하므로 empirical log-likelihood 사용
  • $P_{data}$분포에서 dataset(D)을 구했다고 가정하고, 그 data만 가지고 $P_{θ}$을 학습

• D개의 dataset 내 이미지 input에 대해서만 $P_{θ}$가 최대가 되도록 학습
• 데이터의 숫자가 크지 않을 땐 정확하지 않음
  
  

Empirical Risk Minimization(ERM)

• model이 overfitting이 일어날 수 있음
  • e.g., 강아지 이미지 100개로 학습시킬 때, 모델이 해당 이미지 100개만 다 외워버릴 수 있음
• hypothesis space(model space)를 줄여서 문제 해결
  - 모든 분포의 공간에서 문제를 해결하는 것이 아닌, generative model을 modeling할 수 있는 space를 줄임
  - 전체 generative model의 성능을 떨어뜨릴 수 있음 (underfitting)
  
  
  

---

Latent Variable Models (VAE)

Variational Inference (VI)

→ 찾고자하는 분포가 너무 복잡해서 모델링할 수 없을 때, 간단한 모델로 근사

• Posterior Distribution
  • 데이터가 주어졌을 때, parameter의 확률 분포
  • 대다수 경우 posterior distribution은 구할 수 없음
• Variational Distribution
  • posterior distribution에 근사하는 분포를 구함
  • true posterior와 KL-divergence를 minimize하도록 최적화하는 것이 목표
  • 상대적으로 표현력이 떨어짐

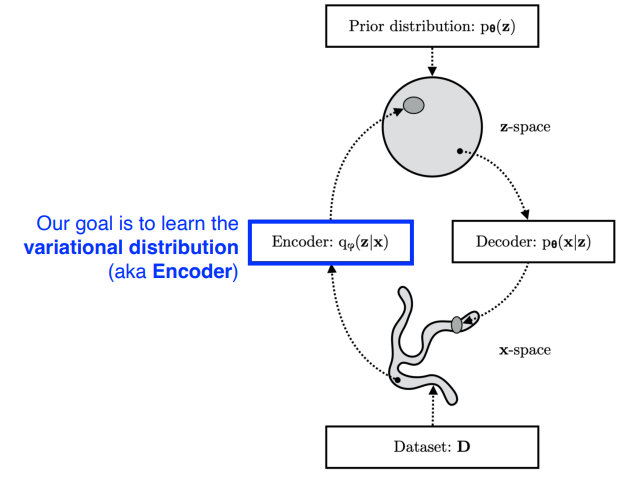
• Prior distribution에서 z를 sampling
  • Prior distribution은 내가 임의로 정해놓은 distribution
  • encoder의 output이 z (latent vector)
• x는 z가 학습된 decoder를 통과한 것으로, x가 원래 data와 비슷하도록 encoder, decoder 학습

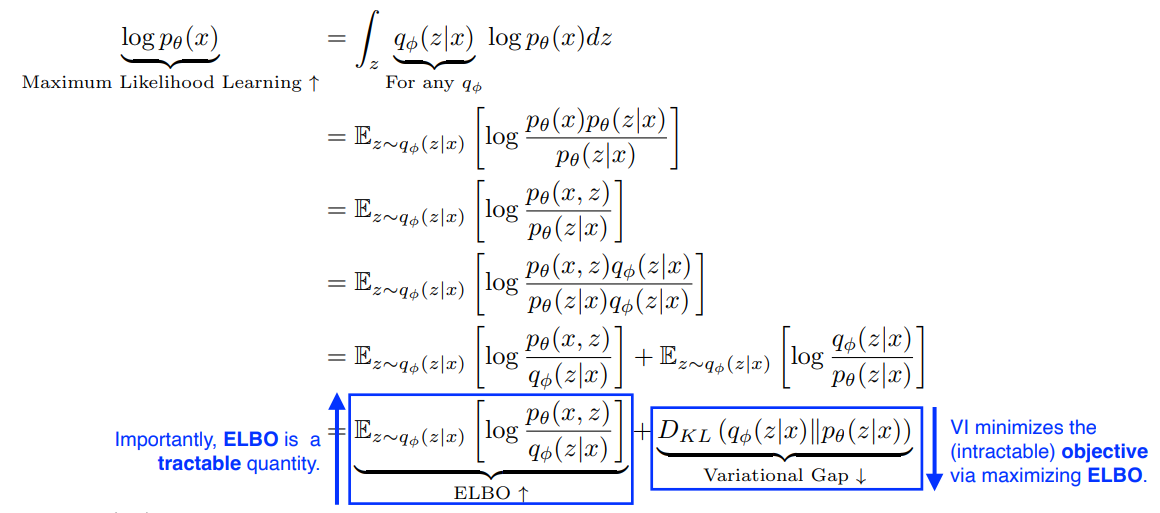
$logp\theta(x)$를 maximize 시키기위해 적분을 하면,

• ELBO (Evidence Lower Bound) & Variational Gap으로 나뉨
• Variational Gap은 posterior $p_{\theta}$가 포함되어 있어 계산이 불가능
• 따라서 ELBO를 Maximize 함으로써 전체 likelihood를 maximize
  
  
  
  

ELBO (Evidence Lower Bound)

$q_ϕ$ : encoder, $p_\theta$ (prior distribution) : decoder

• Reconstruction Term은 encoder와 decoder를 모두 통과한 term

  • Reconstruction loss를 minimize
    
    

$D_{KL}(q_ϕ(z|x)||p(z))$

• encoder와 미리 정해놓은 prior distribution 거리를 최소화
  
  

💡 Auto-encoder를 만든 후 encoder, decoder를 통과하는 Reconstruction loss를 최소화하는 동시에, data x를 encoder에 통과시켜 나온 latent vector z가 미리 정해놓은 prior distribution과 비슷하게 만드는 prior fitting term을 최소화시키는 최적화 방식으로 학습

Limitation

• likelihood evaluate이 어려움
• prior fitting term이 미분가능해야한다
  • 대부분 prior distribution은 gaussian 사용

---

Generative Adversarial Networks (GAN)

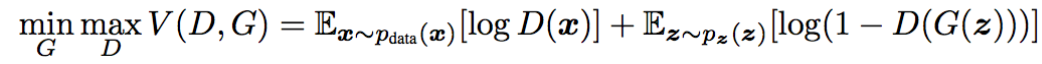
• 두 네트워크 Generator와 Discriminator가 서로를 적대하며 속이는 구조
  
  
  

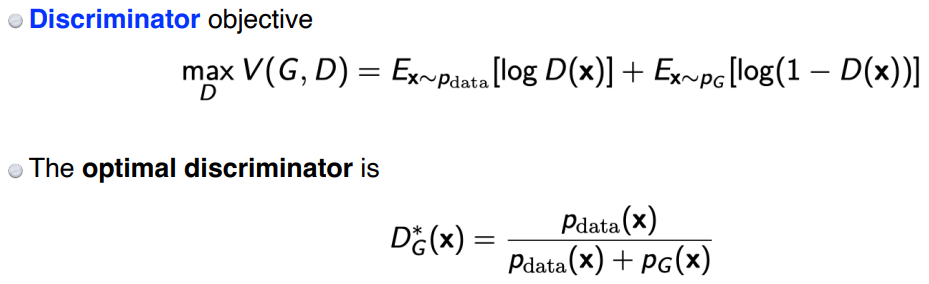
• 전체 식에서 G를 고정하고 D에 대해 풀면 위 그림과 같이 나온다.
  
  
  

• Generator Objective에 앞서 구한 Discriminator Objective를 대입 후 식을 정리하면, $2D_{JSD}[p_{data}, \ p_{G}]-log4$ 식이 도출된다.
  • data의 prior distribution과 Generator의 distribution 사이의 Jenson-Shannon Divergence를 최소화하는 objective를 갖는다.

---

Diffusion Models

→ image를 noise로부터 생성
→ 구현이 어렵고 생성 시간이 오래걸리지만, 성능이 월등함

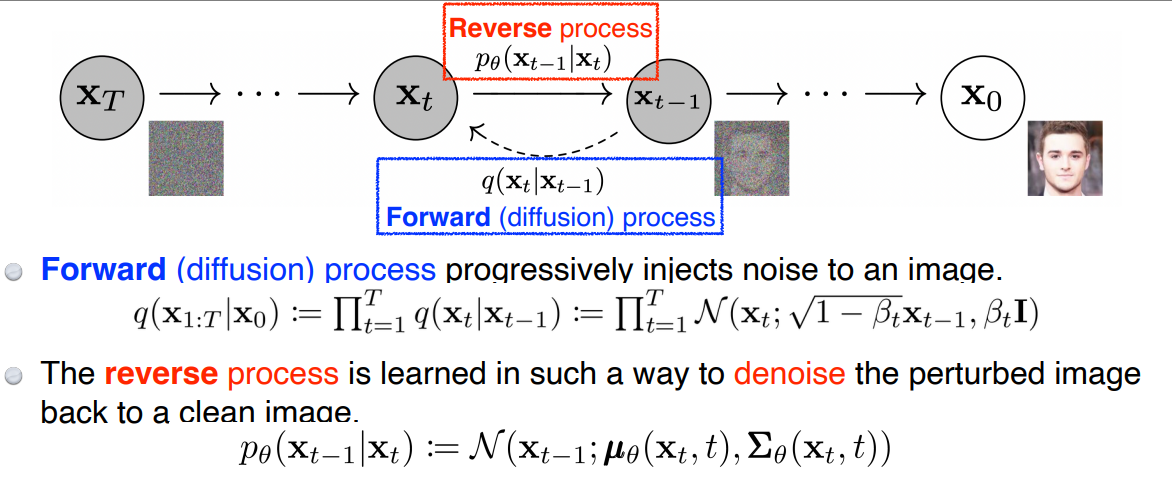
• Forward (diffusion) process
  • 이미지에 noise를 집어넣어 이미지를 점점 noise화 시킴
  • 미리 정해져있음
• reverse process
  • 미리 정해진 방법으로 noise를 집어넣은 이미지에 noise를 없애고 원래 이미지 복원 학습
  • noise를 집어넣는 step이 1000번이었다면, reverse process도 1000번의 step을 가짐

---

---

※ 모든 이미지의 출처는 네이버 커넥트재단 부스트캠프 AI Tech 5기입니다. ※