Seq2Seq - ①

홍찬우·2023년 7월 22일

DL NLP 네이버 부스트캠프

0

Seq2Seq

Seq2Seq 이란?

seq2seq는 입력된 시퀀스로부터 다른 도메인의 시퀀스를 출력하는 모델
- 입력 시퀀스와 출력 시퀀스를 각각 질문과 대답으로 구성하면 챗봇
- 입력 시퀀스와 출력 시퀀스를 각각 입력 문장과 번역 문장으로 만들면 번역기
RNN 기반이며 RNN을 어떻게 조립했냐에 따라 seq2seq 구조가 만들어짐

Seq2Seq 모델 내부 구조

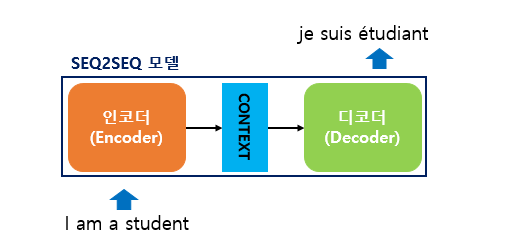
인코더는 입력 문장의 모든 단어들을 순차적으로 입력받은 뒤에 마지막에 이 모든 단어 정보들을 압축해서 하나의 벡터로 만드는데, 이를 컨텍스트 벡터(context vector)라고 함
입력 문장의 정보가 하나의 컨텍스트 벡터로 모두 압축되면 인코더는 컨텍스트 벡터를 디코더로 전송
디코더는 컨텍스트 벡터를 받아서 번역된 단어를 한 개씩 순차적으로 출력

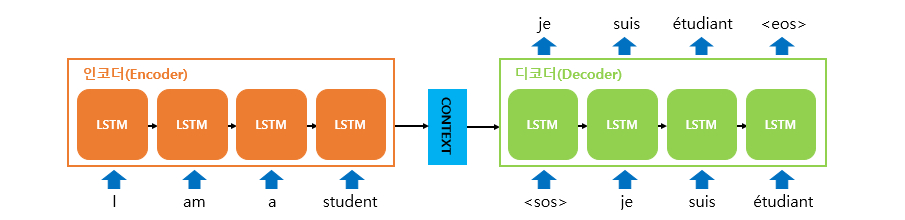
인코더 아키텍처와 디코더 아키텍처의 내부는 사실 두 개의 RNN 아키텍처
- 성능 문제로 인해 바닐라 RNN보다는 LSTM or GRU 사용

인코더

입력 문장은 단어 토큰화를 통해서 단어 단위로 쪼개지고, 단어 토큰 각각은 RNN 셀의 각 시점의 입력
인코더 RNN 셀은 모든 단어를 입력받은 뒤에 인코더 RNN 셀의 마지막 시점의 은닉 상태를 디코더 RNN 셀로 넘겨줌
- 이를 컨텍스트 벡터라고 한다.
- 컨텍스트 벡터는 디코더 RNN 셀의 첫번째 은닉 상태에 사용

※ 은닉 상태 (Hidden State)

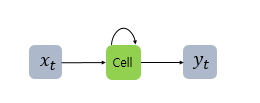
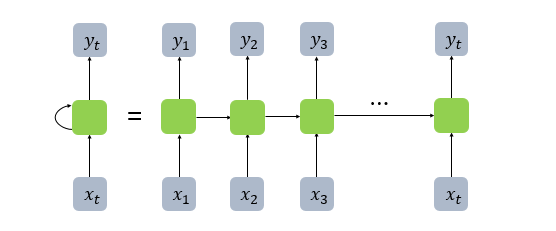
그림의 Cell을 메모리 셀 또는 RNN 셀이라고 표현
- 이전의 값을 기억하려고 하는 일종의 메모리 역할을 수행
- 각각의 시점(time step)에서 바로 이전 시점에서의 은닉층의 메모리 셀에서 나온 값을 자신의 입력으로 사용하는 재귀적 활동
- 메모리 셀이 출력층 방향 또는 다음 시점인 t+1의 자신에게 보내는 값을 은닉 상태(hidden state)
- t시점의 메모리 셀은 t-1시점의 메모리 셀이 보낸 은닉 상태값을 t시점의 은닉 상태 계산을 위한 입력값으로 사용

디코더

디코더는 기본적으로 RNNLM(RNN Language Model)
초기 입력으로 문장의 시작을 의미하는 심볼 <sos>가 들어감

디코더 테스트 과정

디코더는 <sos>가 입력되면, 다음에 등장할 확률이 높은 단어를 예측
첫번째 시점(time step)의 디코더 RNN 셀은 다음에 등장할 단어로 je를 예측
첫번째 시점의 디코더 RNN 셀은 예측된 단어 je를 다음 시점의 RNN 셀의 입력으로 입력
두번째 시점의 디코더 RNN 셀은 입력된 단어 je로부터 다시 다음에 올 단어인 suis를 예측하고, 또 다시 이것을 다음 시점의 RNN 셀의 입력으로 보냄
디코더는 이런 식으로 기본적으로 다음에 올 단어를 예측하고, 그 예측한 단어를 다음 시점의 RNN 셀의 입력으로 넣는 행위를 반복
문장의 끝을 의미하는 심볼인 <eos> 가 다음 단어로 예측될 때까지 반복

Seq2Seq는 훈련 과정과 테스트 과정(또는 실제 번역기를 사람이 쓸 때)의 작동 방식이 다름

훈련 과정
- 디코더에게 인코더가 보낸 컨텍스트 벡터와 실제 정답인 상황인 <sos> je suis étudiant를 입력 받았을 때, je suis étudiant <eos>가 나와야 된다고 정답을 알려주면서 훈련
테스트 과정
- 오직 컨텍스트 벡터와 <sos>만을 입력으로 받은 후에 다음에 올 단어를 예측하고, 그 단어를 다음 시점의 RNN 셀의 입력으로 넣는 행위를 반복

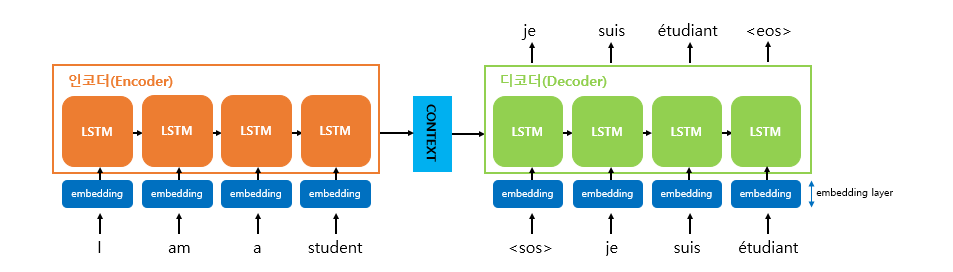
컨텍스트 벡터

컨텍스트 벡터는 사실 인코더에서의 마지막 RNN 셀의 은닉 상태값을 말하는 것
입력 문장의 모든 단어 토큰들의 정보를 요약해서 담고있다고 할 수 있음

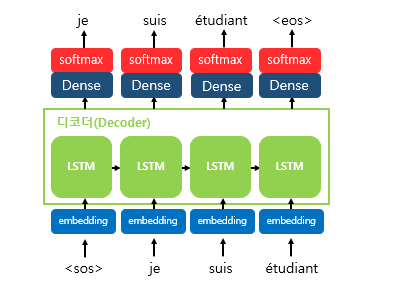
디코더는 인코더의 마지막 RNN 셀의 은닉 상태인 컨텍스트 벡터를 첫번째 은닉 상태의 값으로 사용
디코더의 첫번째 RNN 셀은 이 첫번째 은닉 상태의 값과, 현재 t에서의 입력값인 로부터, 다음에 등장할 단어를 예측
소프트맥스 함수를 통해 출력 시퀀스의 각 단어별 확률값을 반환하고, 디코더는 출력 단어를 결정

Attention

Attention의 아이디어

입력 시퀀스가 길어지면 출력 시퀀스의 정확도가 떨어지는 것을 보정해주기 위해 등장
seq2seq 모델
- 하나의 고정된 크기의 벡터에 모든 정보를 압축하려고 하니까 정보 손실이 발생
- RNN의 고질적인 문제인 기울기 소실(vanishing gradient) 문제가 존재
디코더에서 출력 단어를 예측하는 매 시점마다, 인코더에서의 전체 입력 문장을 다시 한 번 참고
전체 입력 문장을 전부 다 동일한 비율로 참고하는 것이 아니라, 해당 시점에서 예측해야할 단어와 연관이 있는 입력 단어 부분을 좀 더 집중(attention)

Attention Function

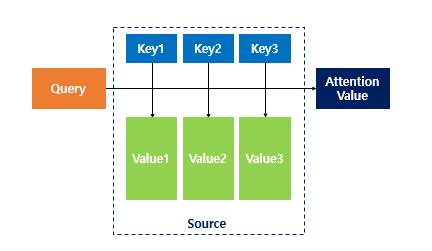
Attention(Q, K, V) = Attention Value

주어진 Query에 대해서 모든 Key와의 유사도를 각각 구함
이 유사도를 키와 맵핑되어있는 각각의 Value에 반영
유사도가 반영된 Value을 모두 더해서 리턴하며, 이를 Attention Value라고 함

Q = Query : t 시점의 디코더 셀에서의 은닉 상태
K = Keys : 모든 시점의 인코더 셀의 은닉 상태들
V = Values : 모든 시점의 인코더 셀의 은닉 상태들

Dot-Product Attention

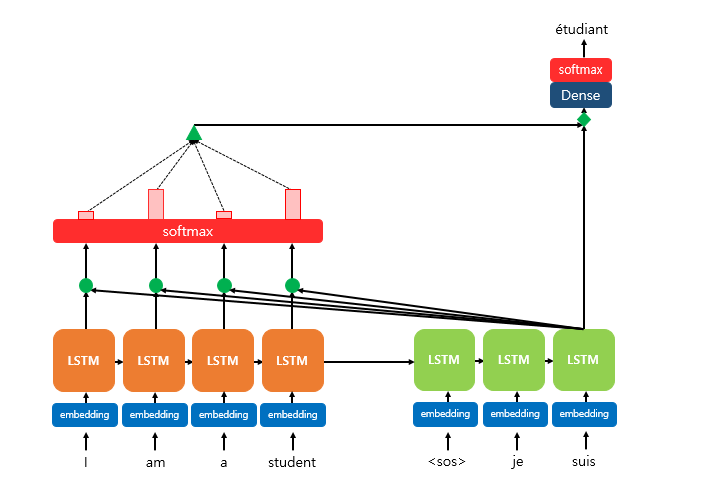
디코더의 세번째 LSTM 셀에서 출력 단어를 예측한다고 하자.
- 디코더의 세번째 LSTM 셀은 출력 단어를 예측하기 위해서 인코더의 모든 입력 단어들의 정보를 다시 한 번 참고
- softmax 위 초록색 삼각형은, 각 입력 단어를 디코더의 예측에 도움이 되는 정도로 수치화하여 측정한 후 이를 하나의 정보로 담아서 디코더로 전송된 것

Process 순서

Attention Score를 구한다.

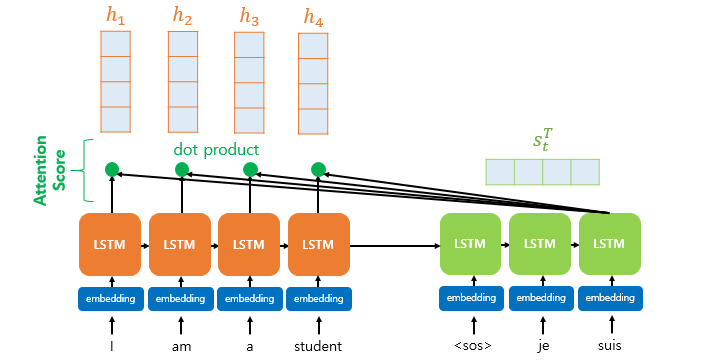
Attention Score
- 디코더의 시점 t에서 단어를 예측하기 위해, 인코더의 모든 은닉 상태 각각이 디코더의 현 시점의 은닉 상태 $s_t$ 와 얼마나 유사한지를 판단하는 스코어 값

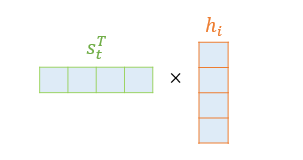
$s_t$ 의 Transpose와 인코더 i번째 time step의 은닉 상태 $h_i$ 와 내적

소프트맥스(softmax) 함수를 통해 어텐션 분포(Attention Distribution)를 구한다.

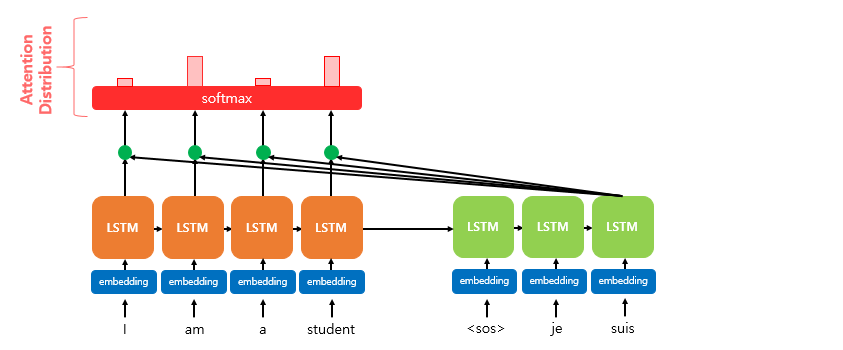
초록색 원은 $e^t$ 이며, 이에 softmax 함수를 적용해 모든 값을 합하면 1이 되는 확률분포를 얻음
- 이를 어텐션 분포(Attention distribution)이라 하며, 각 값은 어텐션 가중치라고 함
- e.g. I, am, a, student 각각에 softmax 함수를 적용해 0.1, 0.4, 0.1, 0.4의 분포를 얻음
디코더 시점 t에서 어텐션 가중치 모음값을 α^t라고 할 때,

\alpha^{t}=softmax(e^{t})

각 인코더의 어텐션 가중치와 은닉 상태를 가중합하여 어텐션 값(Attention Value)을 구한다.

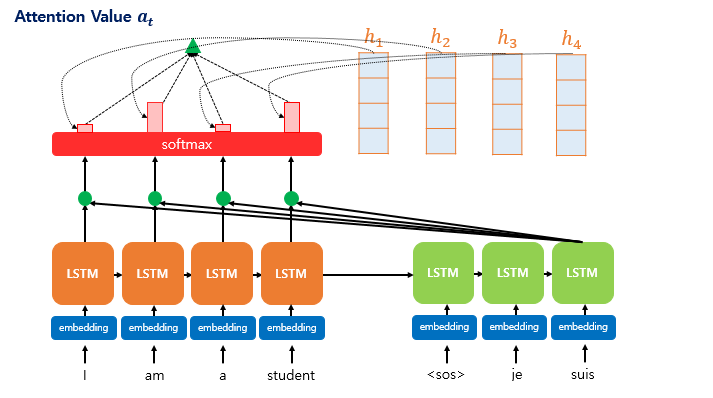
Attention의 최종 결과값을 얻기 위해 각 인코더의 은닉 상태( $h_i$ )와 어텐션 가중치 값( $α^t_i$ )들을 곱하고, 최종적으로 모두 더한다.

a_{t} = \sum^{N}_{i=1}\alpha^{t}_{i}h_{i}

$a_t$ 는 인코더의 문맥을 포함하고 있다고하여, 컨텍스트 벡터(context vector)라고도 함

어텐션 값과 디코더의 t 시점의 은닉 상태를 연결한다.(Concatenate)

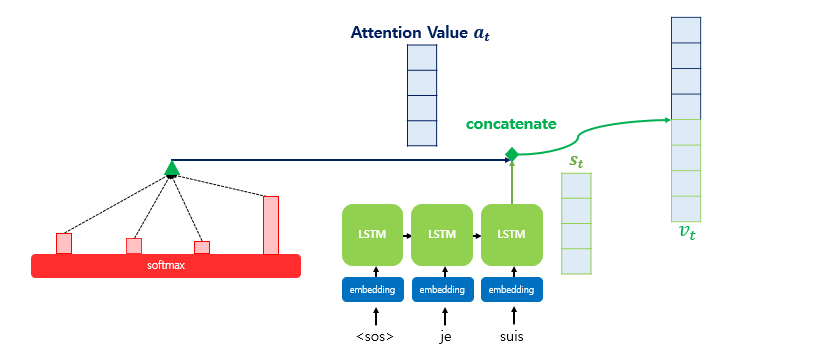
어텐션 값 $a_t$ 와 $s_t$ 를 concat해 벡터 생성( $v_t$ )

출력층 연산의 입력이 되는 $\tilde{s_t}$ 를 계산

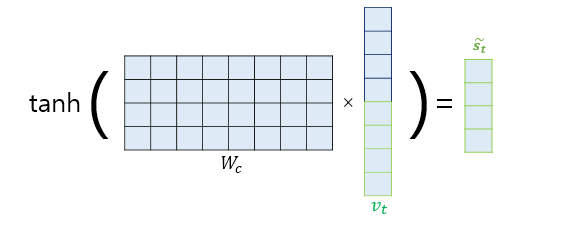
어텐션 메커니즘을 사용하지 않는 seq2seq에서는 출력층의 입력이 t시점의 은닉 상태인 st
어텐션의 경우 $\tilde{s_t}$

\tilde{s_t}=tanh(W_{c}[a_{t};s_{t}] + b_{c})

W $_c$ 는 학습 가능한 가중치 행렬, $b_c$ 는 편향

$\hat{s_t}$ 을 출력층의 입력으로 사용

\hat{y_{t}}=softmax(W_{y}\tilde{s_{t}}+b_{y})

이미지 출처: wikidocs

AI-Kid

이전 포스트

Generative model - ②

다음 포스트

Self Attention & Multi-head Attention - ①

0개의 댓글