이번 시간에는 backpropagation과 Neural Network에 대해서 알아보도록 하겠습니다.

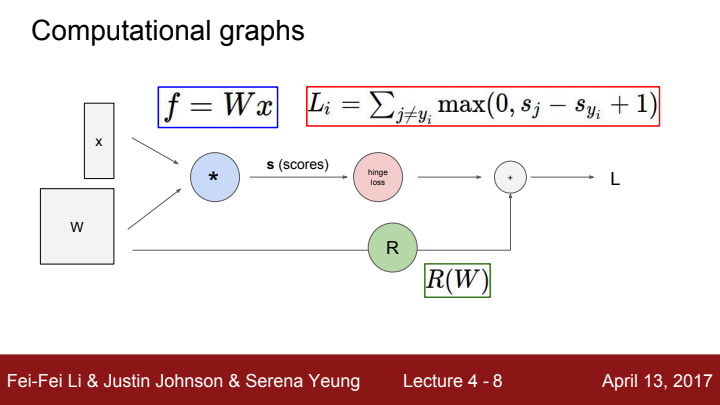
지난 시간에 배운 Loss를 구하는 방법을 graph로 도식화 해보았습니다. W,x를 입력으로 가지는 score function의 출력값을 ground truth 값과 비교하여 sum을 한 data loss term과, W만을 입력으로 가지는 regularization term을 weighted sum하여 전체 loss를 구해줬습니다.

우리가 지난 시간 GD, SGD에 대해 공부하며 W를 gradient값을 가지고 optimization한다고 배웠었죠? backpropagation은 바로 그 gradient를 구하고 optimization을 수행하는 일련의 과정을 뜻합니다.

모델에 input을 넣어 output값을 얻어내는 과정을 forward pass(순전파)라고 하고, output값을 가지고 가중치 W와 bias 값을 학습(업데이트)하는 과정을 backpropagation(역전파)라고 합니다.

---

Backpropagation

backpropagation 과정을 이해하기 위해 간단한 다변수 미적분 문제를 예시로 들고왔습니다. $f(x,y,z)=(x+y)z$ 라는 수식에서 각각 x,y,z 방향으로의 gradient를 구해보겠습니다. 대학교 미분적분학 과정을 수강해보셨다면, 이 문제는 chain rule을 이용해서 풀어야 한다는 사실을 알고 계실 겁니다.

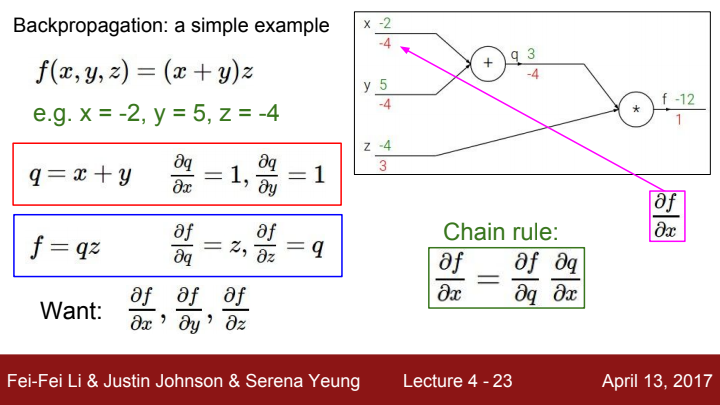
$x+y = q$ 라고 치환하게 된다면 원래의 수식을 $f=qz$ 라는 간단한 형태의 2변수 함수라고 생각할 수 있게 됩니다. $\partial f/ \partial x,\partial f/ \partial y$를 구하기 위해선 우선 $\partial f/\partial q$ 를 구한 뒤 $\partial q/ \partial x, \partial q/ \partial y$ 를 계산하여 multiplication해주면 되겠죠?

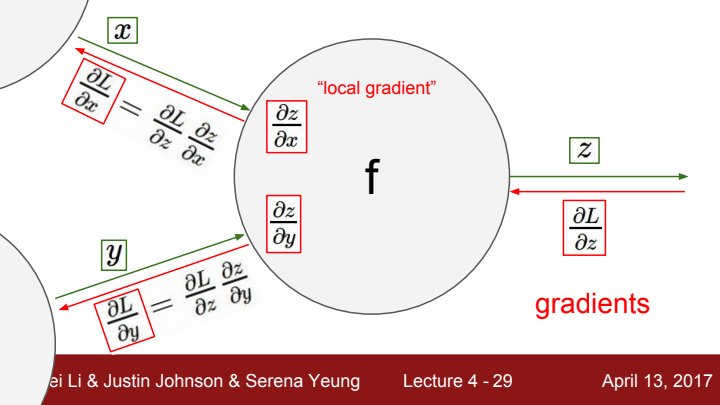
다음과 같이 linear classifier의 score function, Neural Network의 layer, activation function 등 어떠한 입출력 관계를 가지는 함수 하나에서 구한 gradient를 local gradient라고 하고, 최종 출력에서 해당 local gradient 이전 단계까지의 모든 local gradient를 chain rule에 따라 곱해준 값을 upstream gradient라고 합니다. 해당 local에서의 최종 gradient를 구해주려면 upstream gradient와 local gradient를 chain rule에 따라 곱해주면 됩니다.

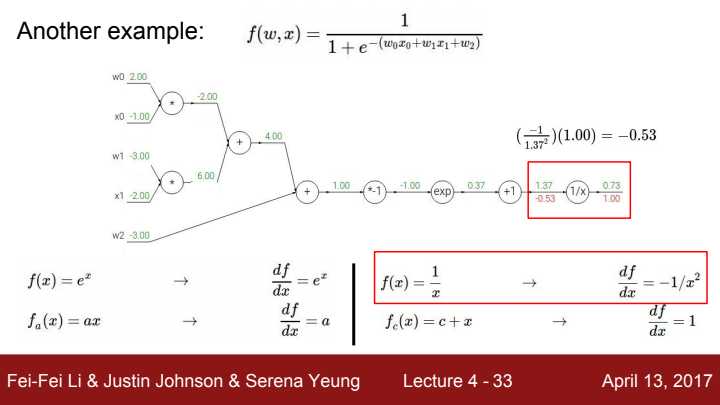
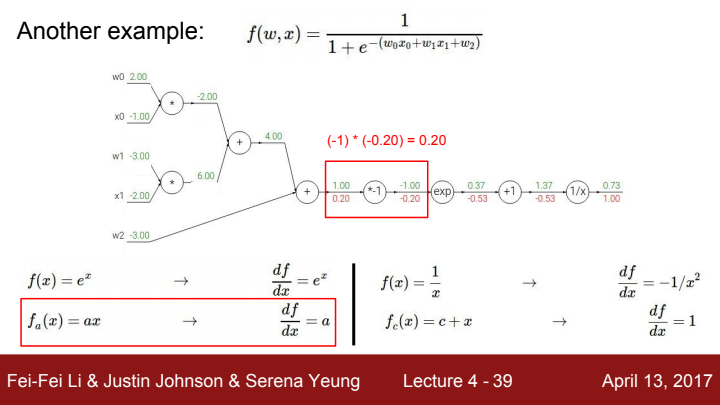
$w_0x_0, w_1x_1, w_2$의 add gate이전까지의 upstream gradient를 순서대로 구하는 과정입니다.

add gate의 gradient는 각 add term들에 대한 편미분이 되기 때문에 각 방향으로의 local gradient는 1이 되겠죠? $w_0x_0 + w_1x_1$을 a라는 term으로 보았을 때, add gate에서 a와 $w_2$방향으로의 local gradient는 모두 1이고 total gradient는 둘 다 upstream gradient값과 동일합니다.

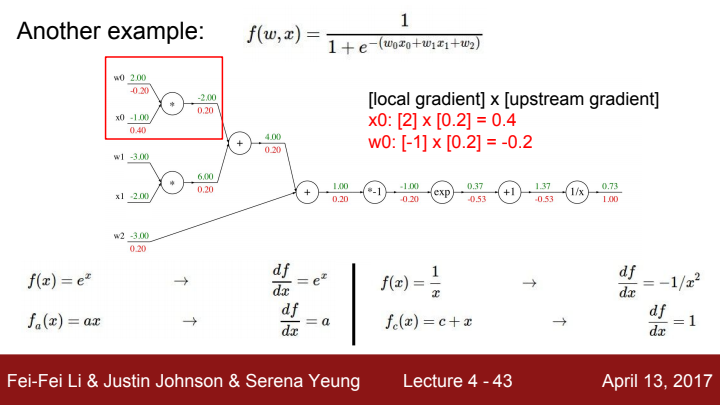
이로써 우리는 $\partial f/ \partial w_0, \partial f / \partial w_2$ 값을 구하게 되었습니다.
($w_1$에 대한 gradient는 $\partial f/ \partial w_0$와 같은 방식으로 구하면 되므로 굳이 ppt에서 보여주진 않고 있습니다)

우리는 이 gradient 값에 음수를 취한 learning rate를 곱해준 만큼 가중치 값을 +해줌으로써 backpropagation을 완료하게 됩니다.

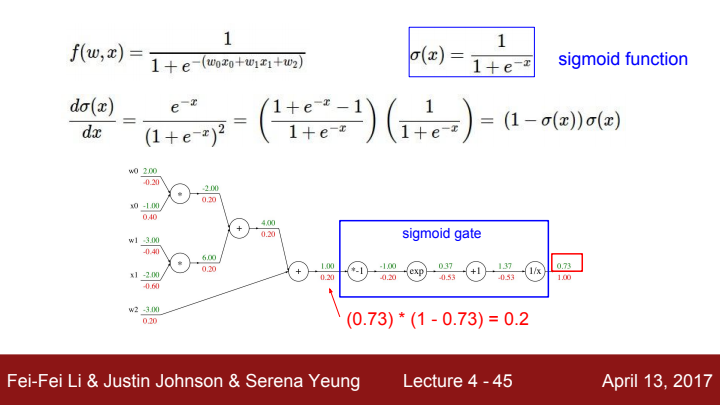
참고로 위에서 사용된 함수 f(w,x)는 sigmoid function이라고 하는 머신 러닝/딥 러닝에서 아주 유명한 함수 중 하나입니다. 이전 강의에서 analytic gradient를 구할 때 명료한 expression들을 미리 정의해두고 거기에 숫자만 대입하는 식으로 gradient를 구해준다고 했었죠? sigmoid function $\sigma$의 gradient에 대한 expression은 $\partial \sigma/\partial x = (1-\sigma(x))\cdot\sigma(x)$입니다. 위 그림에서 이 expression을 사용해줌으로써 더욱 쉽고 빠르게 sigmoid gate의 local gradient를 구해주는 걸 볼 수 있죠?

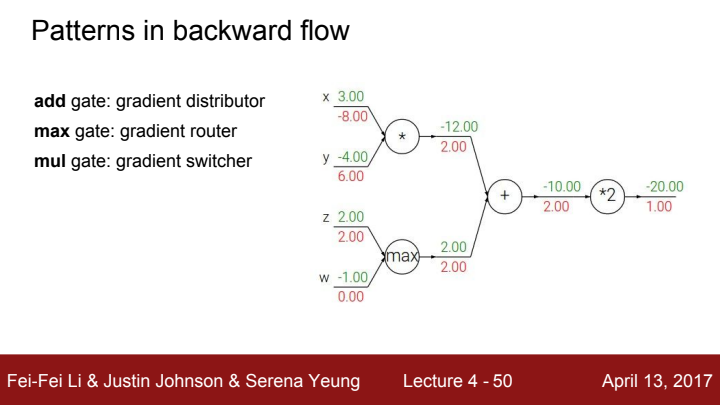
add gate의 경우 앞서 설명드렸다시피, upstream gradient을 input들에게 distribute해주는 역할을 합니다.

max gate의 경우 max gate로 들어온 input값들 중 가장 큰 input에게만 upstream gradient를 전달해주고 나머지 input들의 local gradient를 0으로 만드는 역할을 합니다.

max gate의 router라는 역할에 대해 잘 이해하고 기억해주세요! 이후 배울 강의에서 activation function을 다루게 될 때 이 max라는 함수를 ReLU라는 이름으로 다시 만나게 될 것입니다.

multiplication gate는 들어온 input들의 local gradient를 해당 gate로 들어온 다른 input값으로 switch해주는 역할을 합니다. 위 그림에서의 mul gate를 보면, x에 대한 local gradient가 y값인 -4, y에 대한 local gradient가 x값인 3으로 들어가는 모습을 볼 수 있습니다.

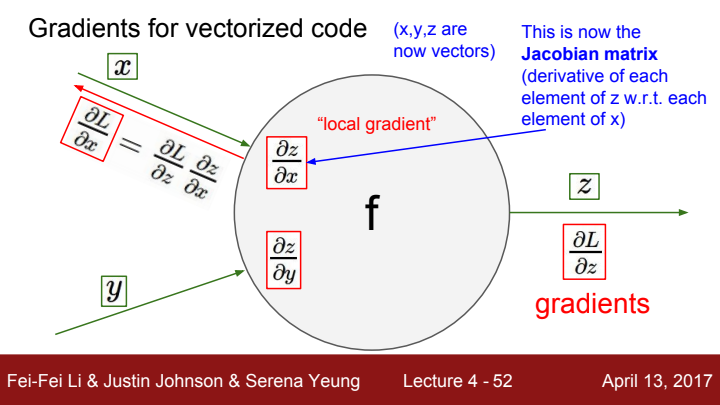
이전까지는 gradient를 구하는 과정에서의 input과 output을 1개짜리 변수라 가정하고 이야기를 나눠보았습니다. 하지만 우리가 딥러닝에서 다룰 이미지나 자연어 같은 input data의 경우 scalar값이 아닌 vector, matrix의 형태입니다.

이 vector에 대한 local gradient는 Jacobian matrix로 표현이 됩니다. Jacobian matrix란 output vector인 $\vec{z}$의 각 element들을 $\vec{x}, \vec{y}$의 각 element들로 편미분한 값들을 모아놓은 matrix를 의미합니다.

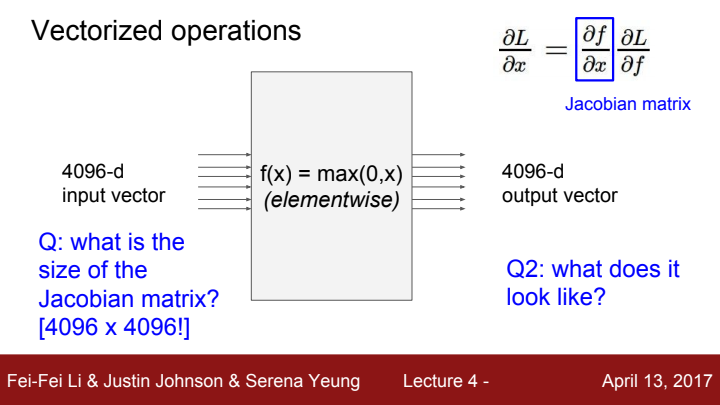
예를 들어 $f(x)=max(0,x)$라는 함수에 대한 Jacobian matrix에 대해 한 번 생각해보도록 하겠습니다. input vector는 4096개의 element를 가진 $\vec{x}$ 하나이고, output vector는 input vector와 같은 사이즈를 가지고 있습니다.

해당 gate에 대한 Jacobian matrix의 size는 input size X output size인 4096X4096이 될 것입니다. $f_1, f_2 ...f_{4096}$에 해당하는 output vector element들을 $x_1,x_2 ... x_{4096}$이라는 input vector의 element들로 편미분해준 값을 구해야 하기 때문이죠.

미니배치의 개수가 예를 들어 100개라고 친다면, 전체 Jacobian matrix의 size는 409600X409600이 되겠네요...이걸 그대로 계산에 사용하겠다 한다면 메모리 낭비가 어마어마할 겁니다.

Jacobian matrix의 형태는 어떻게 될까요? 답은 diagonal(대각) matrix입니다. 왜일까요?

$f(x_1) = f_1$이라고 해봅시다. $f_1$을 $\vec{x}$의 모든 원소들로 편미분했을 때 결과값은 어떻게 될까요? 답은 $\partial f_1/\partial x_1$을 제외한 모든 값들이 0일 것입니다. 당연합니다. 왜냐면 $f_1$은 $x_1$이라는 하나의 element하고만 1대1 대응 관계인 element-wise function이기 때문이죠, $\vec{a}$의 다른 element들과는 독립적인 관계입니다. $x_1^2$를 $x_2$로 미분하면 값이 무엇일까요, 당연히 0이겠죠?

입력의 첫 번째 element는 오직 출력의 첫 번째 element에만 영향을 줄 것입니다.

그렇기에 우리는 실제로 이 Jacobian matrix 전체를 구해줄 필요가 전혀 없고, 그저 출력 값에 대한 입력의 영향만을 가지고 gradient를 계산한다! 라고 생각하시면 됩니다.

이를 잘 곱씹어본다면, 우리가 backpropagation과정에서 구한 local gradient의 matrix size는 input matrix의 size와 동일하겠네요! 출력에 대한 입력의 각 element들의 영향력을 가지고 gradient를 구하기 때문이죠.

vectorized input & output을 하나 예시로 들어 설명해보도록 하겠습니다. 위의 식은 L2 norm(=L2 distance)를 구하는 수식입니다.

2X2 행렬 W와 2X1 벡터인 x를 input으로 받아 forward pass를 하는 모습입니다.

이제부터 backpropagation 과정을 짚어보겠습니다. L2 gate 출력값 $f$를 $q$의 각 원소들 $q_i$로 편미분 해주었을 때의 값은 $2q_i$입니다. 즉 $\nabla_qf=2q$로 표현할 수 있습니다.

$q$는 $W$와 $x$의 dot product입니다. 앞서 scalar input과 output을 가지고 설명했을 때 mul gate는 switcher의 역할을 한다고 이야기했었죠? vectorized된 경우에도 마찬가지입니다.

다만, $W$은 matrix고 $x$는 vector이기 때문에 두 방향으로의 gradient의 Jacobian matrix의 size와 값이 서로 달라지겠죠? 우선 $W$방향으로의 local gradient에 대해 생각해봅시다.

$q =\begin{bmatrix}W_{1,1}x_1+W_{1,2}x_2\\W_{2,1}x_1 + W_{2,2}x_2\\ \end{bmatrix}$

$\partial q_1/\partial W_{1,1} =x_1, \space\space \partial q_1/\partial W_{1,2} = x_2$
$\partial q_1/\partial W_{2,1} =\partial q_1/\partial W_{2,2} = 0$

$\partial q_2/\partial W_{1,1} = \partial q_2/\partial W_{1,2} = 0$
$\partial q_2/\partial W_{2,1} =x_1, \space\space \partial q_2/\partial W_{2,2} = x_2$

gradient는 입력의 각 element들의 영향력을 가지고 구한다고 이야기했었죠?

$\nabla_{w}f = \sum_k(\partial f/ \partial q_k) \cdot(\partial q_k/\partial W_{i,j}) =$

$(2q_1 \cdot x_1 +2q_2 \cdot 0) + (2q_1 \cdot x_2 + 2q_2 \cdot 0) + (2q_1 \cdot 0 +2q_2 \cdot x_1) + (2q_1 \cdot 0 + 2q_2 \cdot x_2)$

$= 2q_1 \cdot (x_1 + x_2) + 2q_2 \cdot (x_1 + x_2)$

$= \begin{bmatrix}2q_1\\2q_2\end{bmatrix} \begin{bmatrix}x_1&x_2\end{bmatrix} = 2q\cdot x^T$

이 expression에 q,x의 수를 대입하면 위의 2X2 matrix를 구할 수 있게 됩니다.

어떤 변수 matrix(vector)에 대한 gradient를 정리한 local gradient의 matrix의 크기는 해당 변수 matrix(vector)의 크기와 동일해야 합니다.

마찬가지의 방법으로 $\nabla_xf$를 구해주었습니다.

참고로 mul gate는 gradient switcher라고 했었죠? 다만 variable이 matrix나 vector가 될 경우 그냥 다른 input값을 받아와 upstream gradient에 곱해주는 것이 아닌, Transpose를 시켜준 뒤 곱해주는 것을 볼 수 있습니다.

그렇다고 scalar의 경우에서처럼 단순히 local gradient를 다른 input의 transposed matrix라고 말하기 어려운 것이, matrix multiplication의 경우 두 matrix의 size가 완벽히 일치하지 않더라도 $(l \times m) \cdot (m \times n)$ 과 같이 앞 matrix의 column과 뒤의 matrix의 row만 일치하면 multiplication이 가능하기 때문이죠.

한 input에 대한 local gradient의 size는 input의 size와 같아야한다고 이야기했었죠? 그래서 local gradient를 단순히 다른 input의 transposed matrix라 말하기엔 무리가 있는 것입니다.

하지만! 다른 input의 transposed matrix가 upstream gradient와 적절하게 mat mul이 되어 total gradient가 된다는 사실은 변함이 없습니다.

지금까지 배운 내용들을 총정리해보았습니다.

---

Neural Networks

다음으론 Neural Network에 대해서 이야기해보도록 하겠습니다.

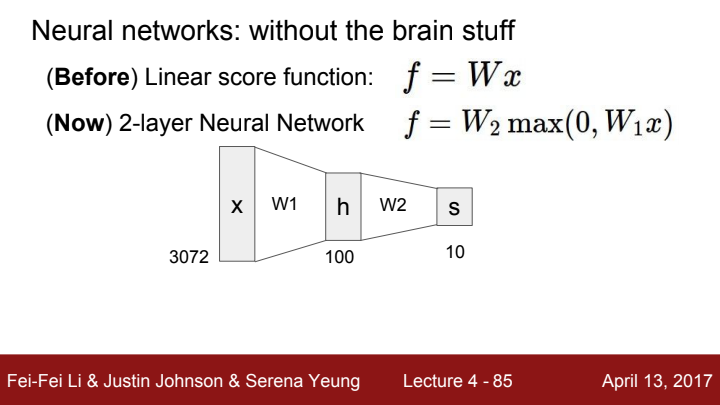
우리가 이전까지 다룬 linear classifier는 $f=W_1x$라는 간단한 하나의 수식이었습니다. 이 classifier의 score값에 $max(0,f)$라는 nonlinear function을 취해준 뒤 $W_2$를 곱하면 어떻게 될까요? 선형 함수와 비선형 함수가 결합된 합성함수가 된다 생각할 수 있겠네요. 이 $f=W_2 \cdot max(0,W_1x)$를 2개의 layer로 이루어진 Neural Network라 볼 수 있습니다.

2중 layer의 Neural Network가 되는데 3-layer Neural Network이 안 될 건 또 없죠? 이렇게 layer의 개수를 우리는 원하는 만큼 마음껏 쌓아나갈 수 있습니다. 당연히 layer의 개수가 늘어날수록 더욱 복잡한 분포의 data를 수월하게 classification할 수 있을 것입니다.

간단한 2-layer Neural Network를 Numpy를 통해 구현한 모습입니다. input data의 size가 64X1000, Weight matrix size가 1000X100, 100X10, output size가 64X10임을 확인할 수 있습니다.

코드를 수식으로 분석해본 결과,
$f_1 = W_1 \cdot x$
$f_2 = W_2 \cdot sigmoid(f_1)$ 이네요.

이 $f_2$값과 실제 y값을 가지고 L2 loss를 구해줍니다.
이후, backpropagation을 위한 expression들을 가지고 analytic gradient를 구한 뒤 1e-4 크기의 learning rate에 gradient를 곱해서 빼주는 모습입니다.

저번 강의에서...
w += -learning_rate * grad
w -= learning_rate * grad
이 두 코드는 같은 동작을 한다고 이야기했었죠?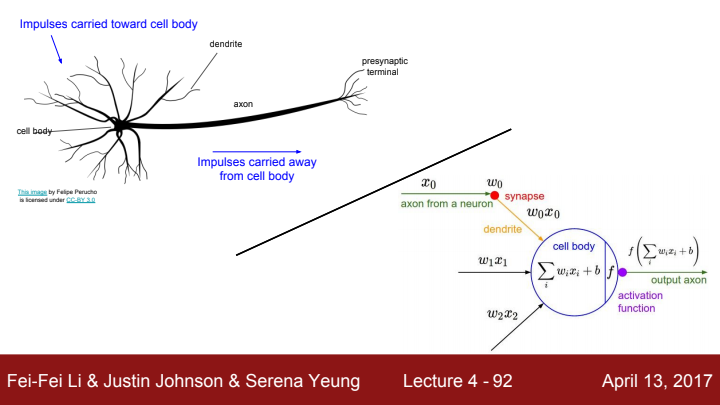

왜 Neural Network는 이름이 Neural Network일까요? 그 이유는 바로 Network의 동작 원리가 뉴런의 동작 원리와 닮아있기 때문입니다.
뉴런의 cell body로 여러 다른 impulse가 synapse를 통해 dendrite를 타고 들어오게 되면, cell body 내부에서 일련의 계산 과정을 거친 새 impulse가 axon을 타고 출력됩니다.

Neural Network에서는 layer가 바로 이 뉴런의 역할을 하게 되는데요, layer에 특정 크기의 matrix가 입력으로 들어오면 가중치(synapse)와의 dot product한 linear function을 cell body에서 수행합니다. 이후 activation function을 거쳐 cell body에서 나온 값을 activation function이라는 nonlinear function의 입력으로 넣어주고 그 함수값을 해당 layer의 출력값으로 삼습니다.

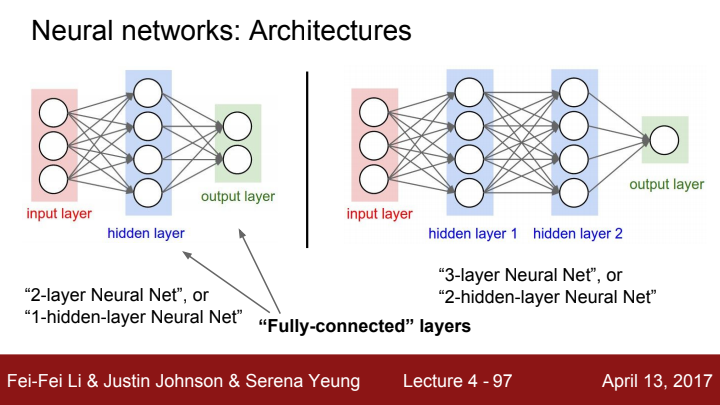
Neural Network의 간단한 Architecture입니다. 이전 layer의 모든 element들이 다음 layer의 모든 원소들과 가중치로 연결되어있는 모습을 볼 수 있습니다. 우리는 이러한 layer를 Fully-Connected(FC) layer라고 부릅니다. input layer와 output layer 사이에 존재하는 layer들은 hidden layer라고 부릅니다.

여기서 질문, activation function은 왜 필요한 걸까요? 차후 강의에서 설명하겠지만, linear function만 가지고는 아무리 layer를 쌓은들 복잡한 data에 대한 task를 수행할 수 없습니다.

x라는 어떤 변수에 제가 순차적으로 1을 곱하고, 그 곱한 값에 2를 곱해주고, 또 그 곱한 값에 3을 곱해주고... 이 행위를 10번 반복한다고 쳐봅시다. 저는 곱하기라는 행위를 10번이나 수행했지만, 이는 사실 x에 10!이라는 수를 한 번 곱한 것과 다를 바가 없습니다. linear function들 사이사이에 activation function이라는 nonlinear function이 끼워져 있어야만 복잡한 계산을 Network가 수행할 수 있는 것입니다.

activation function들의 종류로는 다음과 같은 함수들이 있습니다. 각각의 activation function들에 대한 설명은 이후 강의에서 더욱 자세히 다뤄보도록 하겠습니다.

오늘은 backpropagation 과정과 Neural Network에 대해 배워보았습니다. 다음 강의에서는 Convolution layer를 사용하는, CNN에 대해 배워보도록 하겠습니다.