1.2 Row Reduction and Echelon Forms

조범희 선생님의 선형대수학개론 강의를 듣고 공부하며 정리한 내용입니다.
정말 좋은 강의힙니다. 강추합니다. 링크

A nonzero row or column

at least one element should be nonzero

A leading entry of row

the leftmost nonzero entry

$\begin{bmatrix} 1 & -2 & 1 & 0\\ 0 & 2 & -8 & 8\\ 0 & 0 & 0 & 77\\ 92 & 0 & -1 & 5\\ 0 & 0 & 1 & 0\\ \end{bmatrix}$

leading entry or row 1 : 1

leading entry or row 2 : 2

leading entry or row 3 : 77

leading entry or row 4 : 92

leading entry or row 5 : 1

Echelon Form

1. All nonzero rows are above any rows of all zeros.
2. Each leading entry of a row is in a column to the right of the leading entry of the row above it

$\begin{bmatrix} l & * & * & * & * & *\\ 0 & l & * & * & * & *\\ 0 & 0 & l & * & * & *\\ 0 & 0 & 0 & 0 & l & *\\ 0 & 0 & 0 & 0 & 0 & l\\ \end{bmatrix}$

l stands for leading entry
can be any number (zero or non-zero)

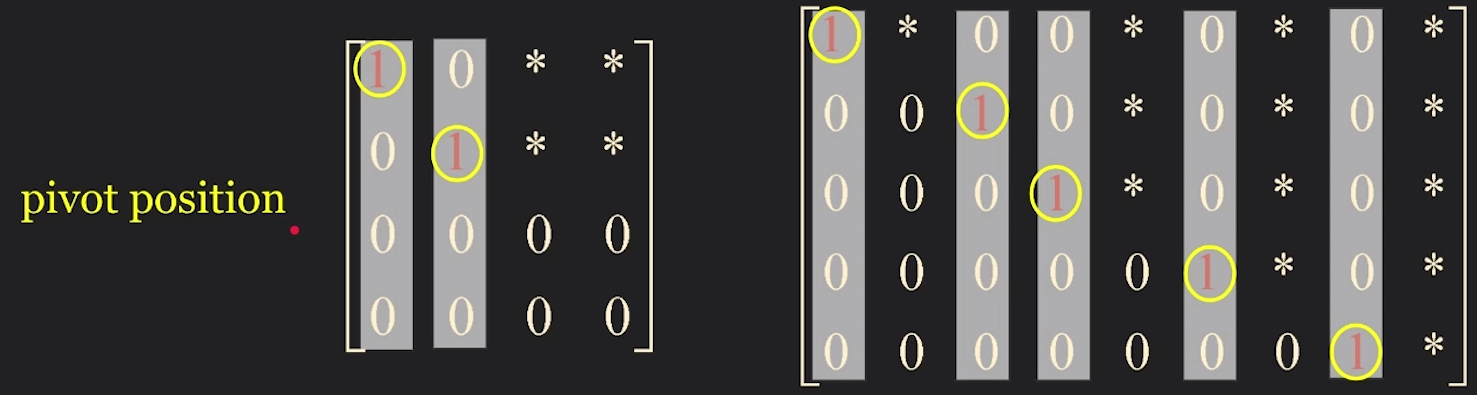
Reduced Echelon Form

1 & 2. Same with Echelon Form

3. The leading entry in each nonzero row is 1.

4. Each leading 1 is the only nonzero entry in its column.

$\begin{bmatrix} 1 & * & 0 & 0 & * & 0 & * & 0 & *\\ 0 & 0 & 1 & 0 & * & 0 & * & 0 & *\\ 0 & 0 & 0 & 1 & * & 0 & * & 0 & *\\ 0 & 0 & 0 & 0 & 0 & 1 & * & 0 & *\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & *\\ \end{bmatrix}$

l stands for leading entry
position of leading entry is called pivot posiotion

Theorem 1. Uniqueness of the Reduced Echelon Form

Each matrix is row equivalent to one and only one reduced echelon matrix.

(4단원쯤 가면 증명한다고 함)

 

Row reduction algorithm

Step1. begin with the leftmost nonzero column

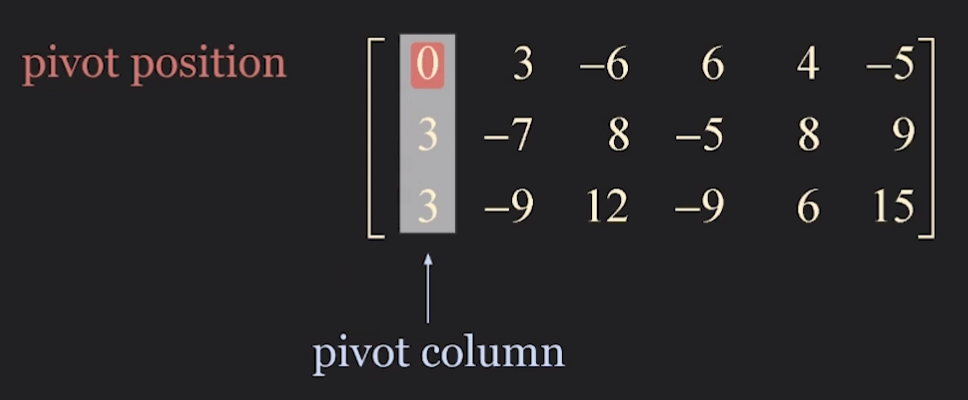
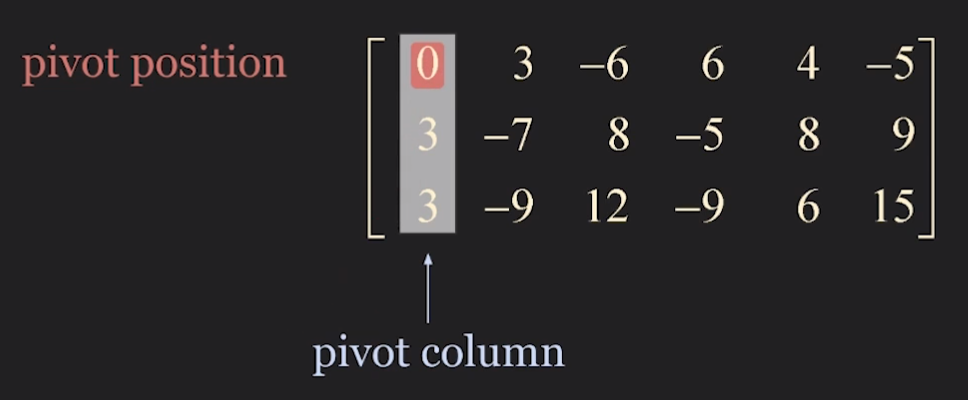
Step 2. select a nonzero entry in the pivot column as a pivot. If necessary, interchange rows to move this entry into the pivot position

Step3. row replacement to create zeros in all positions below the pivot

~ means row equivalent

Step4. apply steps 1-3 to the submatrix that remain

The combination of steps 1-4 is called forward phase

Echelon Form!

 

To make Reduced Echelon Form

Step5. Beginning with the rightmost pivot and working upward and to the left, create zeros above each pivot. If a pivot is not 1, make it 1 by a scaling operation.

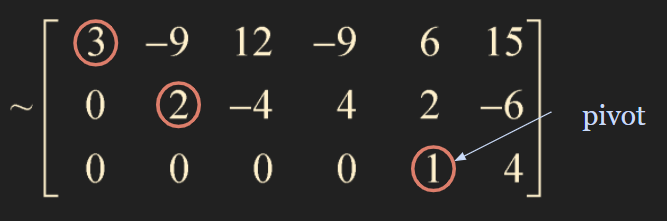
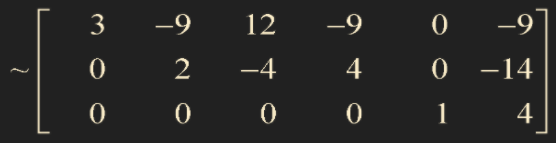
Step 5 is called backward phase

Reduced Echelon Form!

 

Solution of linear systems

$\begin{bmatrix} 1 & 0 & -5 & 1\\ 0 & 1 & 1 & 4\\ 0 & 0 & 0 & 0 \end{bmatrix}$ This matrix has infinite number of solutions

ex. $\begin{bmatrix} 6\\ 3\\ 1 \end{bmatrix}$$\begin{bmatrix} -9\\ 6\\ -2 \end{bmatrix}$

몇몇 변수를 free 로 하고, free variable 을 이용해 다른 변수를 표현함으로써 solution을 나타낼 수 있다. 이때, free가 아닌 variable은 basic variable 이라고 하는데, leading position에 해당되는 변수들을 basic variable로 잡고, 나머지는 모두 free variable로 잡는 것으로 약속함으로써 통일성있게 solution을 나타낼 수 있다. 이와 같은 solution 을 general solution 이라고 한다.

 

Theorem 2. Existence and Uniqueness Theorem

A linear system is consistent if and only if the rightmost column of the augmented matrix is not a pivot column - that is, if and only if an echelon form of the augmented matrix has no row of the forms

$\begin{bmatrix}\ 0\ \cdots\ 0\quad b\ \end{bmatrix}$ with b is nonzero

If a linear system is consistent, then the solution set contains either (i) a unique solution, when there are no free variables, or (ii) infinitely many solutions, when there is at least one free variables.

If a matrix is in row-echelon form, then the first nonzero entry of each row is called a pivot, and the columns in which pivots appear are called pivot columns.