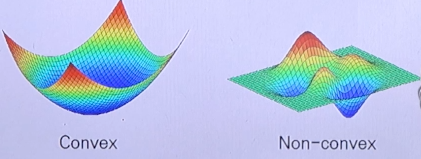
1. Challenges of Optimization Problem
- 다음과 같은 경우는 최적의 해를 찾는 경우가 어렵거나 불가능할 수 있다.
- 훨씬 많은 parameter를 가진 이차 방정식
- logistic regression 같은 모델
- Nonlinear functions (ex: neural networks)
2. 최적의 근사치를 찾기 위한 접근 방법들
- Gradient descent method(경사 하강법)
- Newton method
- Gauss-Newton
- Levenberg-Marquardt
- BFGS
- Conjugate gradient
- Etc
3. What is Gradient?
- Gradient는 벡터이다.
- 각 변수별로 편비분한 값들을 모아둔 것이 Gradient가 된다.
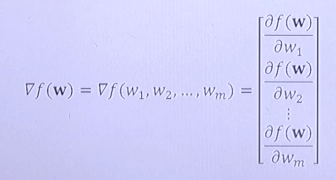
- 특정한 지점에서 각 변수로 편비분을 한 값들을 합친 f가 해당 지점에서의 Gradient가 된다.
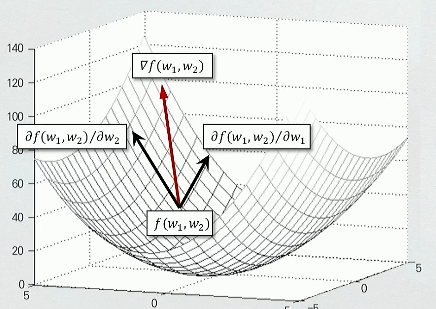
- E(w)가 최소가 되는 w 지점을 찾아야 한다.
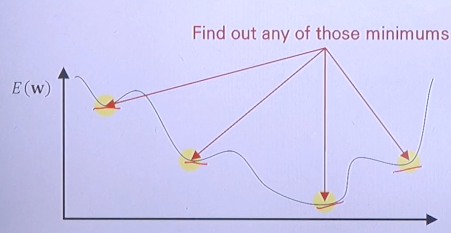
4. w를 어떻게 update하는가?
- 랜덤하게 처음 지점 W0을 선택한다.
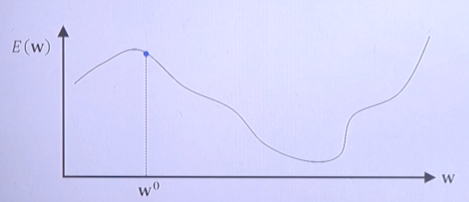
- Error function의 값을 update하였을때 이전 Error 값 보다 적은 방향으로 update하여야 한다.
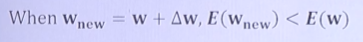만약 E(w)이 미분이 가능하다면 미분한 값(기울기)를 통해 오른쪽, 왼쪽을 선택할 수 있다.
- 기울기가 음수라면 오른쪽으로, 양수라면 왼쪽으로 이동한다.
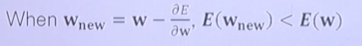
- 이때 기울기 앞에 learning rate라는 변수를 둬서 변화하는 기울기 값에 임의의 값을 곱해서 조절할 수 있다.
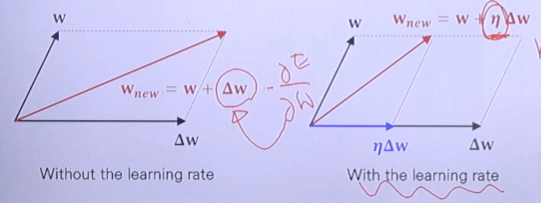
- 업데이트되는 정도를 조절하기 위해서 learning rate를 도입한다.
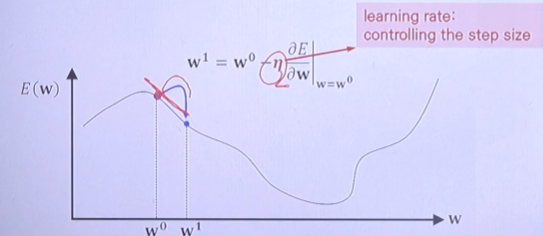
- E(w)가 zero가 되는 방향으로 계속 진행한다.
5. What is the Learning Rate?
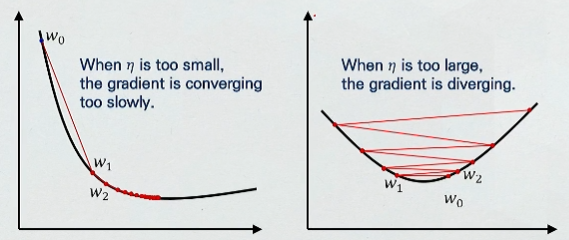
- n은 setp size나 step length를 조절하기 위함이다.
- 너무 작은 n은 지나치게 많은 시간을 걸릴 수 있고 너무 큰 n은 학습이 전혀 이루어지지 않고 발산하는 단점이 있을 수 있다.
- n은 학습 과정에 있어서 중요한 역할을 한다.
5. Gradient Descent(GD) Pseudo-code
- pseudo-code :
- Multiple parameters들에 대해서는 각 W0, W1들에 대해 parallel하게 비교해나간다.
6. Summary
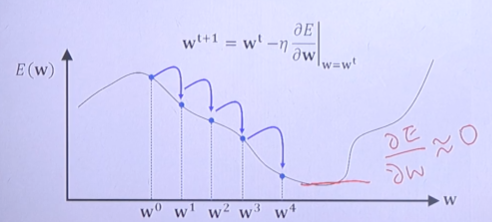
- Simple concept : 임의의 w값에 대해서 Gradient(Slope)가 0이 되는 방향으로 점차 나아가는 최적화 기법이다.
- Process
- Initial point W0을 지정한다.
- 주어진 지점에서 편미분을 함으로써 어느 방향으로 나아갈지 선택한다.
- 이동폭을 위해 Learning rate를 지정한다.
- Position을 update한다.
- 주어진 조건을 만족할때 까지 2-4를 반복한다.
(조건 : W(t)에서의 Gradient 값이 0에 근사할때까지)
heec.choi