📌: https://arxiv.org/abs/2311.17245
methods 위주로 리뷰

Abstract

LightGaussian은 3D Gaussian Splatting의 저장 공간 문제를 해결하기 위해 개발된 새로운 기술이다.

• 불필요한 가우시안 제거
• 효율적인 형태로 전환해서 장면 재구성에 기여하지 않는 가우시안 줄임
  • 가우시안 벡터 양자화로 데이터를 더 낮은 비트 폭으로 저장
  • FPS 크게 향상시켜 복잡한 데이터셋에서의 성능 극대화

LightGaussian은 평균 15배 이상의 압축률을 달성했고, 시각적 효과를 유지하면서도 더 낮은 저장 공간 을 사용한다.

Methods

overview of LightGaussian

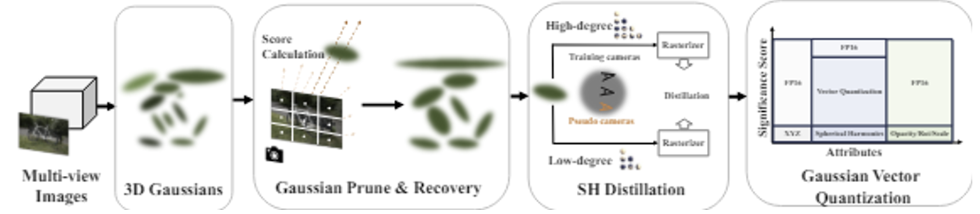
3DGS 모델은 multi-view 이미지로 훈련되고, SfM point clouds에서 초기화된다. 희소 포인트를 수백만 개의 가우시안으로 확장해서 장면이 잘 표현된다.

Gaussian Prune과 Recovery 사용해서 가우시안 수를 줄이고, SH Distillation을 사용하여 중복 SH를 제거하고, 중요한 조명 정보는 보존한다. Vector Quantization은 코드북 초기화 및 할당을 포함하여 모델 대역폭을 줄이는 데 사용된다.

LightGaussian은 먼저 훈련 데이터에 대해 각 가우시안의 전역 중요도를 계산하고, 중요도가 낮은 가우시안을 제거한다. 합성된 가상 뷰를 사용한 증류가 도입되어 SH를 컴팩트한 형식으로 전환한다. Vector Quantization은 더 낮은 비트 폭에서 가우시안을 저장하는 데 사용된다.

3.1. Background: 3D Gaussian Splatting

3DGS는 가우시안을 사용하여 장면을 모델링하는 explicit point 기반 3D 장면 표현이다. SfM으로 생성된 sparse point cloud에서 초기화되며, 가우시안 밀도 증가를 적용해서 작은 규모의 geometry를 불충분하게 다루는 가우시안 수를 증가시킨다.

각 가우시안은 공분산 행렬 Σ와 중심점 X(가우시안의 평균값)을 갖는다. Σ는 미분 최적화를 위한 스케일링 행렬 S와 회전 행렬 R로 분해될 수 있다.

복잡한 방향성은 구면조화(SH)로 모델링된다. 차수 D는 SH의 복잡성을 결정하는데, 차수가 높을수록 세밀하게 모델링할 수 있지만 계산과 저장 부하가 증가한다.

Splatting으로 3D 가우시안에서 2D 이미지를 rendering한다.

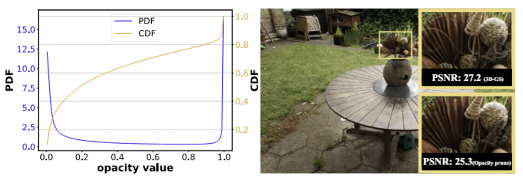
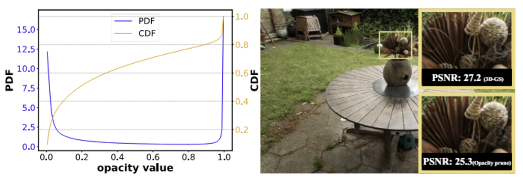
(opacity는 투명도, PSNR은 피크 신호 대 잡음비)

• 위 이미지(PSNR: 27.2)
  • 3DGS으로 렌더링된 이미지, 높은 PSNR
• 아래 이미지(PSNR: 25.3)
  • 불투명도 기반으로 중요하지 않은 가우시안 제거한 후 렌더링
  • PSNR 낮아짐, 디테일 감소

Zero-shot 불투명도 기반 Pruning

• 많은 가우시안이 낮은 불투명도 값을 가진다
• 불투명도를 pruning의 지표로 단순히 사용하면 중요하지 않은 가우시안 제거하게 된다
  • 근데 이렇게 하면 렌더링된 이미지의 세부 사항이 손실돼서 PSNR 값 낮아진다

3.2. Gaussian Pruning & Recovery

Gaussian densification (가우시안 밀도 증가):

• 초기 SfM 포인트 클라우드를 복제하고 분할하여 불충분한 coverage 문제를 해결한다.
• 소규모 geometry와 세부적인 장면을 더 잘 모델링할 수 있다
• 재구성 품질을 향상시킨다.

Problem:

• 최적화 후 가우시안의 수가 수천개에서 수백만개로 증가한다.
  • 큰 저장 공간 요구하게 된다

Solution: pruning

불필요한 가우시안을 제거하면서도 모델의 성능을 유지해야 한다. 중복 가우시안을 식별하는 것이 중요하다. 단순히 불투명도에 기반하여 pruning 하면 모델의 성능이 저하될 수 있다.

Global Significance Calculation

가우시안의 중요성을 평가할 때 불투명도에 의존하는 대신 3D 가우시안이 view frustum 내에서 평가되고, rendering을 위해 카메라 view point로 투영된다.


Global significant score (GS)

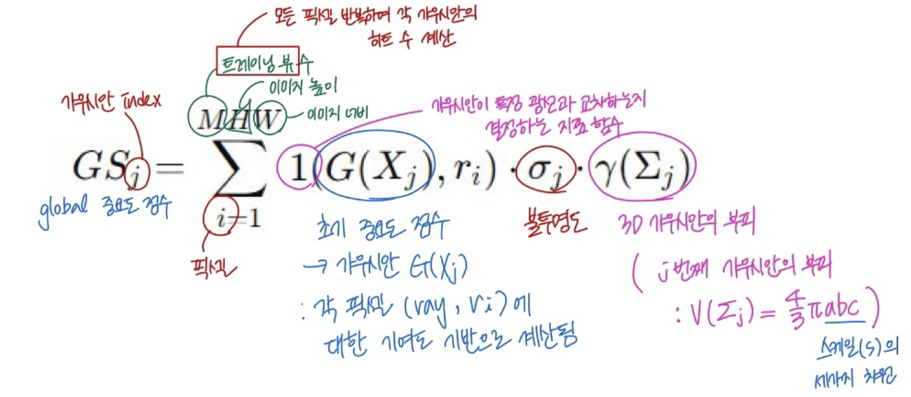
가우시안 부피를 사용하면 배경 가우시안의 중요성을 과장해서, 복잡한 geometry를 모델링할 때 중요한 가우시안을 많이 제거할 수 있다. 따라서 더 adaptive 방법으로 부피를 측정한다.

adaptive way (β=3)

가우시안 부피는 상위 90%의 가장 큰 가우시안에 의해 정규화되고, 범위는 0에서 1 사이로 유지 돼서 3DGS의 과도한 중요도 할당을 방지한다.

Gaussian Co-adaptation

: pruning 후 남은 가우시안들을 최적화하여 모델의 성능을 유지하는 방법

계산된 GS(global 중요도 점수)를 바탕으로 모든 가우시안에 순위를 매기는데. 순위는 점수가 낮은 가우시안을 pruning할 수 있는 기준이다. (= 점수가 낮은 가우시안은 모델 성능에 덜 기여하기 때문에 pruning 대상이다)

pruning 후 남은 가우시안들은 추가적인 densification 없이 최적화된다. co-adaptation은 각 가우시안이 최적의 상태로 조정되어 전체적인 모델의 성능을 유지하는 데 도움이 된다.

Photometric loss는 이미지의 픽셀 값 차이를 기반으로 손실을 계산하는 방법이다. 원래의 훈련 view를 사용하여 5000번 반복해서 손실을 최소화하도록 한다.

3.3. Distilling into Compact SHs

압축되지 않은 Gaussian Splat 데이터는 상당한 양의 구면 조화(SH) 계수를 포함하고 있다. SH 수를 줄이면 공간을 절약할 수 있지만 표면 광택이 크게 감소하고, 뷰 포인트가 변경될 때 반사 변화의 분산(variance in specular reflections)에 영향을 미친다.

모델의 크기와 장면 모델링 품질 사이의 균형을 맞추기 위해 고차수 SH에서 저차수 SH로 지식을 전이하는 distillation process을 제안하였다. (증류 과정: teacher model → student model 지식을 전이)

증류 손실 함수 (H: 이미지 높이, W: 이미지 너비, C: 픽셀 강도)
두 모델 간의 예측된 픽셀 강도 차이를 최소화하는 방식으로 정의

Synthesize Pseudo Views

뷰포인트가 변경되면 물체 표면에서 반사되는 광선이 달라진다. 뷰포인트를 추가적으로 샘플링하여 훈련 데이터에 새로운 시점을 도입하면 반사 특성을 더 잘 포착할 수 있다. 가우시안 분포를 사용하여 새로운 카메라 위치를 샘플링하고, 일관된 카메라 뷰 방향을 유지한다.

새로 생성 된 의사 카메라 위치 = 훈련 카메라 위치 + N

N은 평균이 0이고 분산이 σ^2인 가우시안 분포를 나타내고, 이는 새로운 위치를 생성하기 위해 원래 위치에 더해진다.

3.4. Gaussian Attributes Vector Quantization

벡터 양자화는 voxel을 압축 코드북으로 클러스터링한다. 높은 압축률을 달성할 수 있지만, 가우시안 속성을 양자화하는 것은 점 기반 표현의 non-Euclidean 성질 때문에 어렵다. 특히 위치, 회전, 스케일과 같은 속성에 양자화를 적용하면 정밀도와 정확도가 저하될 수 있다.

SH 계수에 벡터 양자화가 적용되는데, 사전 계산된 중요도 점수를 활용하여 rendering 품질 손실과 압축률 간의 균형을 맞추는 데 중점을 둔다. 벡터 양자화를 적용할 때, SH에서 가장 중요하지 않은 요소들을 선택적으로 양자화한다. K 평균을 통해 C(코드북)를 초기화하고, 반복적으로 G(가우시안 집합)의 배치를 샘플링하여 유클리드 거리로 가장 가까운 코드에 연결한다. 이동 평균 규칙을 통해 각 ck를 업데이트한다.

λd = 0.8은 갑쇠값을 나타낸다.
5000번 동안 반복하며 코드 부분을 fine tuning 하며, 가우시안-코드북 매핑을 고정한다. 훈련 뷰에서 추가적인 클론이나 분할 작업 없이 photometric loss를 최소화한다.