앞에서 살펴봤던 LDA는 이전 LSA의 단점을 개선하고 보완하여 나온 알고리즘이다.
그렇다면, LSA는 무엇인지 앞서 간단하게 설명하고자 한다.
LSA (Latent Semantic Analysis)
잠재 의미 분석(LSA), 이는 Topic Modeling 과정에서 쓰이는 기법이다.
기본적으로 단어의 빈도 수를 이용한 수치화 방법.
이 알고리즘은 'NLP(자연어 처리)'를 근원으로 한다.
BoW에 기반한 DTM이나 TF-IDF는 기본적으로 단어의 빈도 수를 이용한 수치화 방법이기 때문에, 단어의 의미를 고려하지 못한다는 단점이 있었고, 이를 위한 대안으로 LSA라는 방법이 나왔다.
우리는 이 LSA, 즉 잠재(Latent) 의미를 제대로 이끌어내기 위해서는, 나름대로의 차원 축소 기술이 필요한데, 이 때 Truncated SVD가 사용되기 때문에, SVD를 알고 넘어가야할 필요가 있다.
이를 사용함으로써 기존의 행렬에서는 드러나지 않았던 심층적인 의미를 확인할 수 있게 된다.
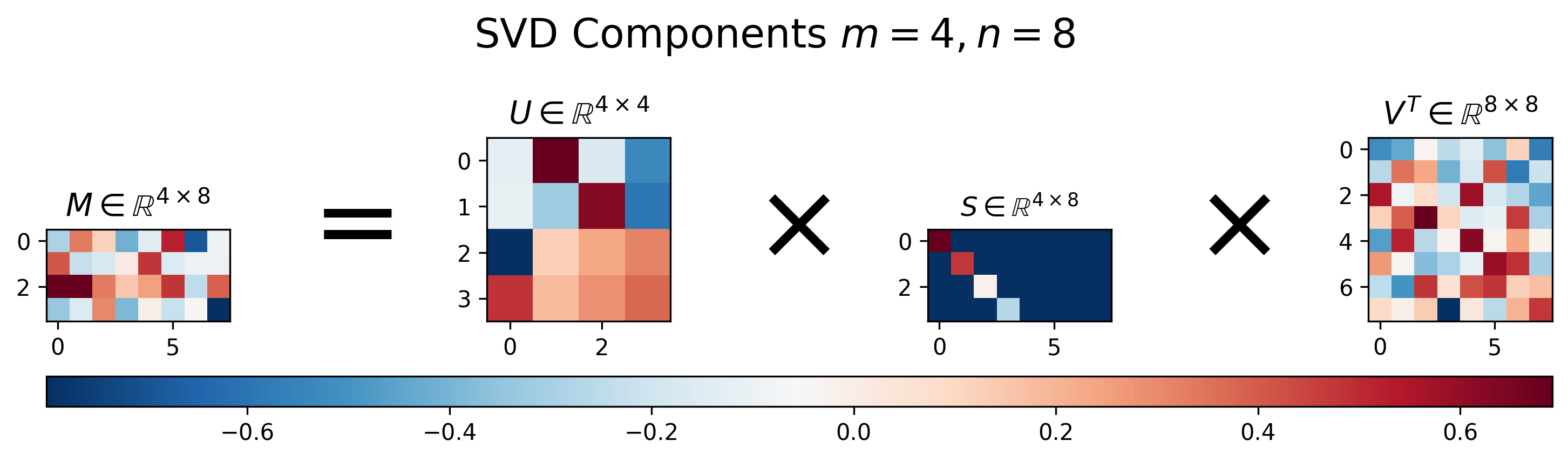
SVD (Singular Value Decomposition)
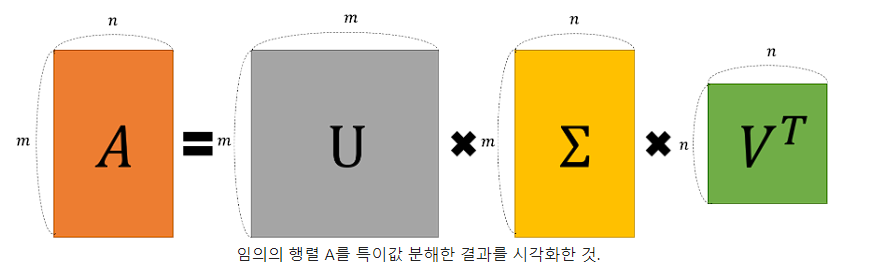
임의의 차원의 행렬 에 대하여 다음과 같이 행렬을 분해할 수 있다는 ‘행렬 분해(decomposition)’ 방법 중 하나.
: rectangular matrix
: orthogonal matrix
: diagonal matrix
: orthogonal matrix
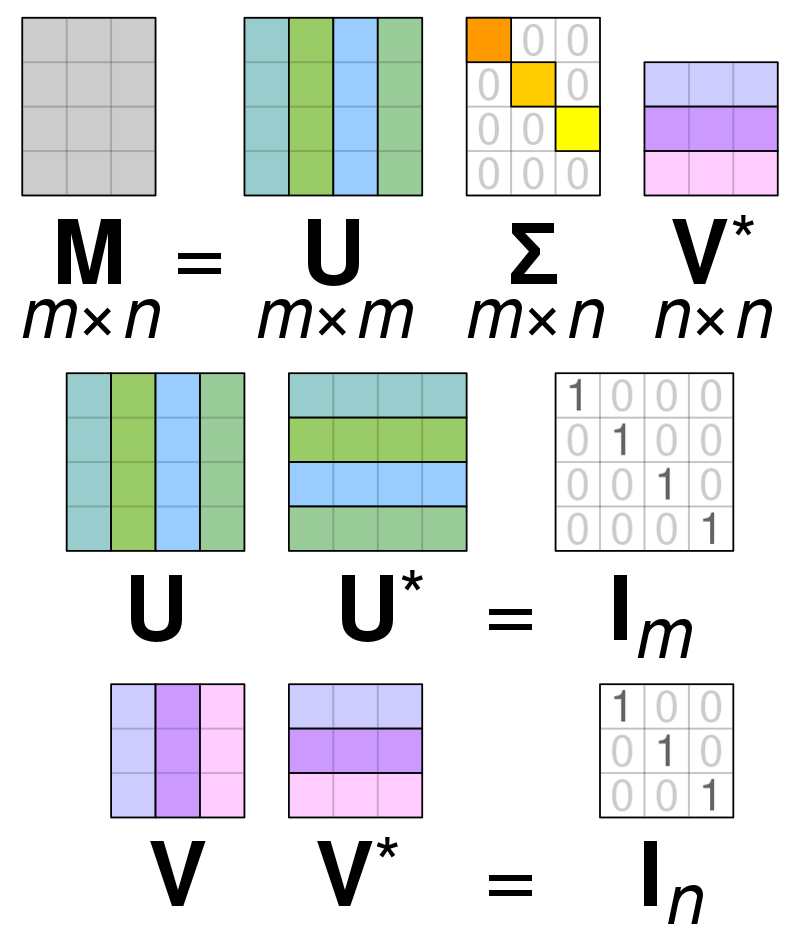
SVD라는 방법을 이용해 라는 임의의 행렬을 여러 개의 행렬과 동일한 크기를 갖는 여러 개의 행렬로 분해해서 생각할 수 있는데, 분해된 각 행렬의 원소의 값의 크기는 의 값의 크기에 의해 결정된다.
→ SVD를 이용해 임의의 행렬 를 정보량에 따라 여러 layer로 쪼개서 생각할 수 있게 해준다.
특이값 분해는 분해되는 과정보다는 분해된 행렬을 다시 조합하는 과정에서 그 응용력이 빛을 발한다.
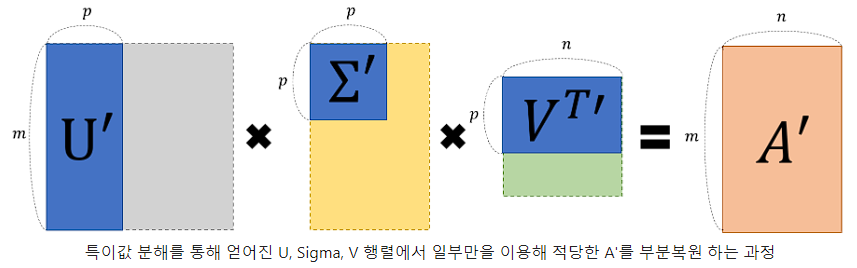
기존의 , , 로 분해되어 있던 행렬을 특이값 개만을 이용해 라는 행렬로 ‘부분 복원’ 할 수 있다.
특이값의 크기에 따라 의 정보량이 결정되기 때문에, 값이 큰 몇 개의 특이값들을 가지고도 충분히 유용한 정보를 유지할 수 있다.
SVD에서의 여러가지 관계
( 또는 )
Full SVD vs Truncate SVD
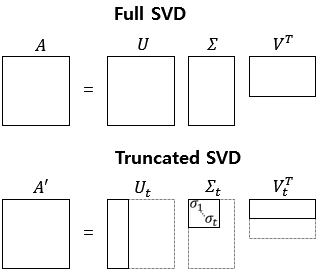
Full SVD
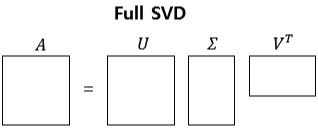
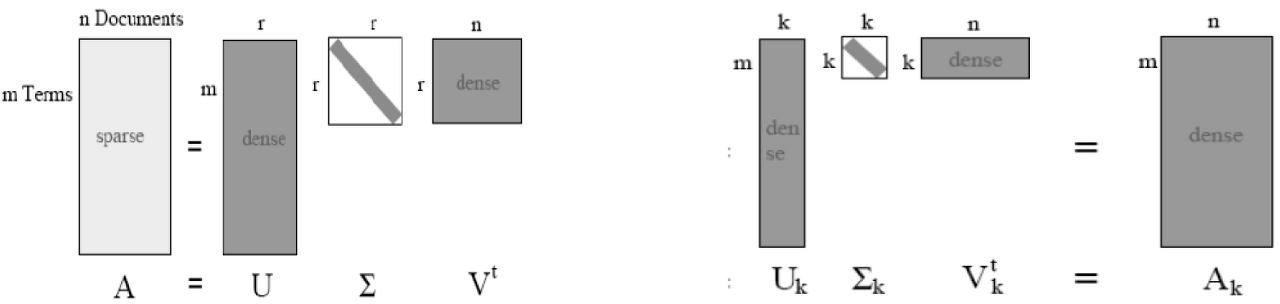
행렬 를 x 크기인 , x 크기인 , x 크기인 로 특이값 분해(SVD)하는 것.
실제로 Full SVD를 사용하는 경우는 드물다.
Truncated SVD
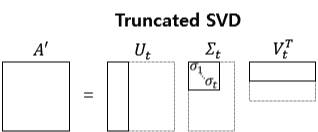
의 크기는 x ,
의 크기는 x ,
Transpose of 의 크기는 x
( : 상위 개만 추출한다는 의미)
의 비대각 부분과 대각 원소 중 특이값이 0인 부분을 모두 제거하고, 제거된 에 대응되는 와 원소도 함께 제거해 차원을 줄인 형태로 SVD를 적용
→ ∑의 대각 원소 중 상위 몇 개만 추출하고 여기에 대응하는 U와 V의 원소도 함께 제거해 차원을 줄인 것.
<예시 데이터>
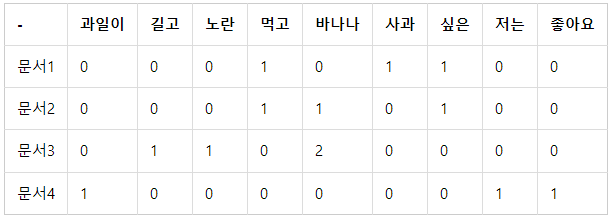
축소된 는 문서의 개수 × 토픽의 수 의 크기
즉, 의 각 행은 잠재 의미를 표현하기 위한 수치화 된 각각의 문서 벡터
축소된 VT는 토픽의 수 × 단어의 개수의 크기
의 각 열은 잠재 의미를 표현하기 위해 수치화된 각각의 단어 벡터
Full SVD는 분해를 해도 모든 원소가 남아있기 때문에 원본 행렬 로 원복이 가능하지만, Truncated SVD는 원소를 손실하기 때문에 원복이 불가하지만, 근사하게는 일치.
가 클수록 원래의 행렬 와 가까워지며, 가 작아질수록 원본 행렬 와 차이가 많이 난다.
SVD는 매우 많은 피처를 가진 고차원 행렬을 저차원 행렬로 분리하는 행렬 분해 기법이다.
특히 이런 행렬 분해를 수행하면서 원본 행렬에서 잠재된 요소를 추출하기 때문에, 토픽 모델링(NLP)이나 추천 시스템에 활발하게 사용된다.
ref ) https://angeloyeo.github.io/2019/08/01/SVD.html
https://wikidocs.net/24949
https://bkshin.tistory.com/entry/NLP-9-%EC%BD%94%EC%82%AC%EC%9D%B8-%EC%9C%A0%EC%82%AC%EB%8F%84%EB%A5%BC-%ED%99%9C%EC%9A%A9%ED%95%9C-%EC%98%81%ED%99%94-%EC%B6%94%EC%B2%9C-%EC%8B%9C%EC%8A%A4%ED%85%9C
https://darkpgmr.tistory.com/106
https://www.fun-coding.org/recommend_basic6.html