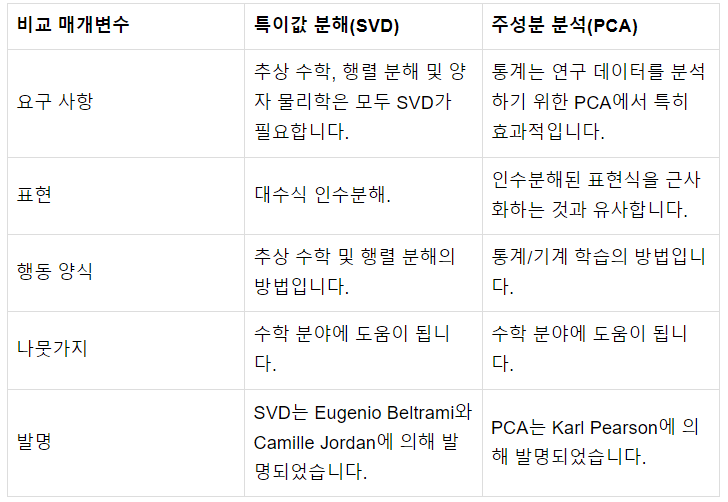
SVD를 이용한 차원 축소는 데이터를 개별적으로 압축하지만, PCA는 데이터를 집합적으로 압축한다.
SVD는 수학적 알고리즘, PCA는 통계 기법
SVD는 데이터 기반 푸리에 변환 일반화인 반면, PCA를 사용하면 데이터를 기반으로 하는 계층적 좌표 시스템을 사용하여 데이터 세트의 통계적 변동을 나타낼 수 있다.
-
SVD는 대수식을 인수분해하는 것과 직접 비교할 수 있는 반면, PCA는 '가장 큰' 항을 유지하고 더 작은 모든 항을 제거하여 인수분해된 명령문을 근사화하는 것과 같다.
-
SVD의 값은 일관된 숫자이며 인수분해는 이를 분해하는 과정인 반면 PCA는 주요 측면을 결정하는 통계/기계 지능 방식이다.
-
행렬을 직교 정규 영역으로 분해하는 것을 SVD라고 하는 반면, PCA는 SVD를 사용하여 계산할 수 있지만 가격이 더 높다.
-
SVD는 데이터 수집을 위한 수치 선형 대수학에서 가장 광범위하게 사용되는 다목적 유용한 기능 중 하나인 반면, PCA는 통계에 대한 많은 이론을 도입한 잘 정립된 방법이다.
-
SVD는 저명한 알고리즘 중 하나인 반면, PCA는 차원 축소 접근 방식이다.
따라서 SVD는 고정 요인을 사용하여 대수식을 인수분해하는 반면, PCA는 전체 변동을 최대화하는 데이터의 기본 패턴을 평가하기 위한 통계/기계 지능 기술이다.
특이값 분해(SVD)는 고유값 분해(EVD)처럼 행렬을 대각화하는 한 방법이다.
그런데, 특이값 분해가 유용한 이유는 행렬이 정방행렬이든 아니든 관계없이, 모든 x 행렬에 대해 적용 가능하기 때문.
PCA 는 고유값 분해(EVD)는 기본적으로 정방행렬을 반드시 필요로 하며, 새로운 축을 만들어 고유 벡터의 새로운 관점으로 바라보는 것이었다면, SVD 는 정방행렬이 아니라 직사각형 행렬일 때 사용한다.
ref) https://darkpgmr.tistory.com/110
https://askanydifference.com/difference-between-singular-value-decomposition-svd-and-principal-component-analysis-pca-with-table/