#26 Optimization

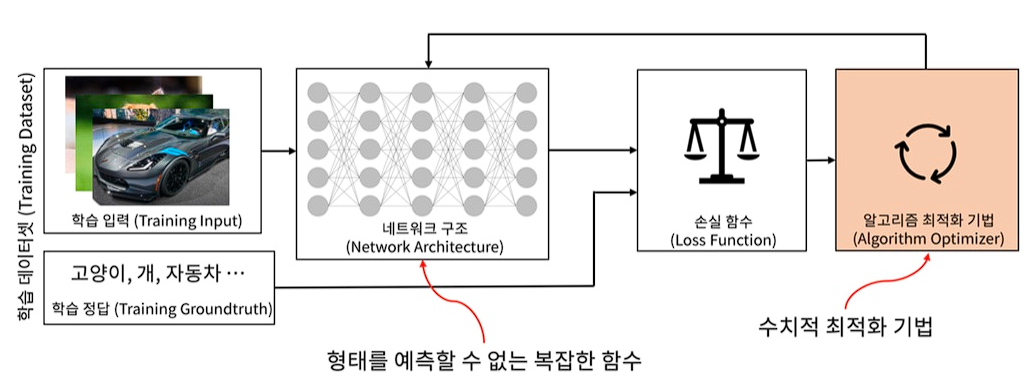
머신러닝에서 모델을 학습할 때는 비용(cost) 즉, 오류를 최소화하는 방향으로 진행이 된다.

비용이 최소화되는 곳이 성능이 가장 잘 나오는 부분이며, 가능한 비용이 적은 부분을 찾는 것이 최적화(Optimization)이고, 일반화(Generalization)의 방법이다.

Optimization (최적화)

최적화(optimization) 문제란 어떤 목적함수(objective function)의 함수값을 최적화(최대화 또는 최소화)시키는 파라미터(변수) 조합을 찾는 문제

→ 우리가 원하는 어떤 조건(함수값을 최소화 또는 최대화)을 만족시키는 최적의 파라미터(변수) 값을 찾는 문제를 말한다.

모든 파라미터(변수)에 대해 일차 이하의 다항식으로 구성되면 선형 최적화(linear optimization)
$f(x_1,x_2,...,x_m) = b + a_1x_1 + a_2x_2 + ... + a_mx_m$ 등

그 외의 경우를 비선형 최적화(nonlinear optimization)
$f(x,y) = ysinx + x$,
$f(x,y) = x^2 + y$,
$f(x,y) = xy - 1$ 등

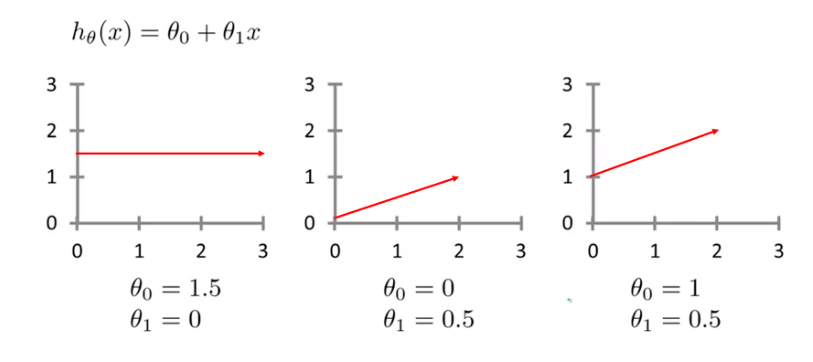
가설 함수의 형태를 결정짓는 것은 매개변수(parameter) 라 부르는 $θ$ 이다. 우리는 이 $θ$값을 적절하게 조정하여 실제값 $y$에 가장 근접한 가설함수* 를 Training set을 이용하여 도출해야 한다.

※ 가설 함수 $f(x) = h_θ(x)$
(가설 함수 = 추정 함수)

$h(x)-θ$ 은 '가설 함수와 실제 $y$ 값의 차이', 이것을 최소화 하는 것이 목표

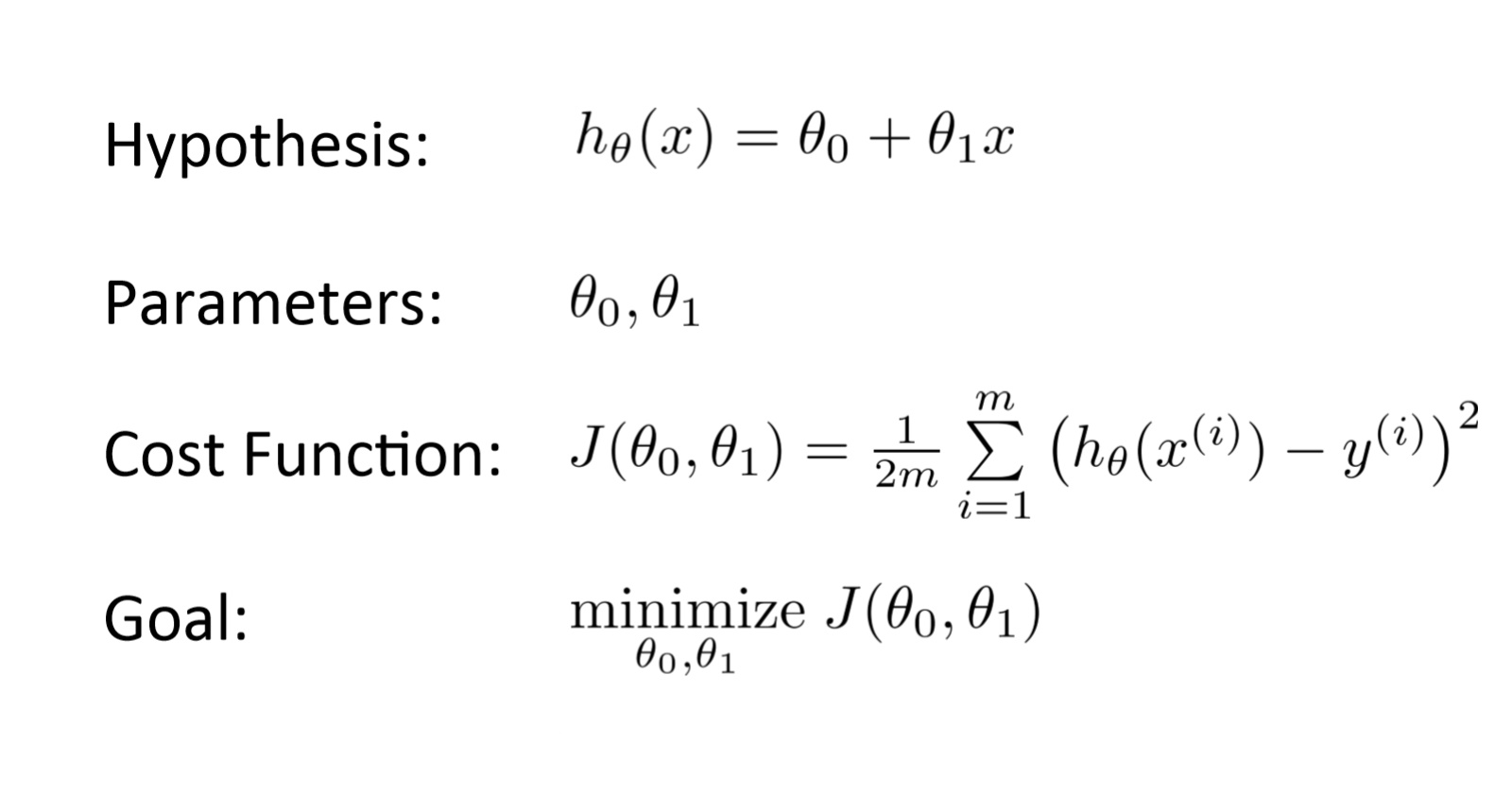
원리

가장 기본적인 원리는 현재 위치에서 함수값이 감소(최대화 문제라면 증가)하는 방향으로 조금씩 조금씩 파라미터 값을 이동해 나가는 것.

즉, 한걸음을 내딛은 후 그 위치에서 어느 방향이 가장 내리막 길인지를 봐서 그 방향으로 한 걸음을 내딛고, 또 다시 그 위치에서 가장 내리막 방향을 찾고... 하는 과정을 더 이상 내려갈 수 없는 곳에 다다를 때까지 반복.
(대표적으로 이 방식을 Gradient Descent 라고도 한다.)

그리고 이런 과정을 반복하다 보면 언젠가는 함수값이 최소화(최대화)되는 지점을 발견할 수 있을 것이라는 원리.

Loss function (손실 함수)

한 데이터 포인트에서의 (예측-실제)의 차이 = '놓친 정도'를 표현한 함수
(여러 종류의 함수가 존재할 수 있음)

→ 순간 순간 데이터 포인트마다 loss function에 의한 loss (놓침) 값

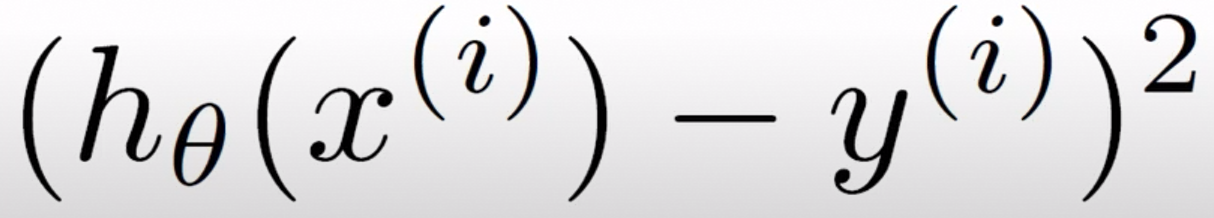
Cost Function (비용 함수)

데이터 전체에서 예측 값과 실제 값 차이의 평균

→ 학습이 완료된 후에는 cost function으로 총 cost (비용) 확인

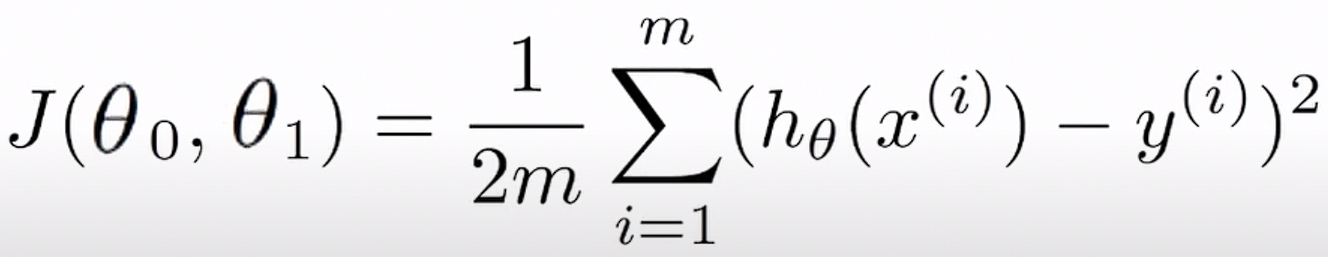
그냥 사용하면 오차가 양수 혹은 음수가 될 수 있으므로 제곱

목적

Training set은 $1$부터 $m$까지 존재하기에 각각의 차이를 모두 더하여 평균을 내어, 이 평균이 최소가 되게 만드는 $θ$를 구하는 것.

(이 때 $m$이 아닌 $2m$으로 나눈 이유는 미분을 했을 때 내려오는 $2$와 자연스럽게 나눠지게 하기 위함.)

시각화

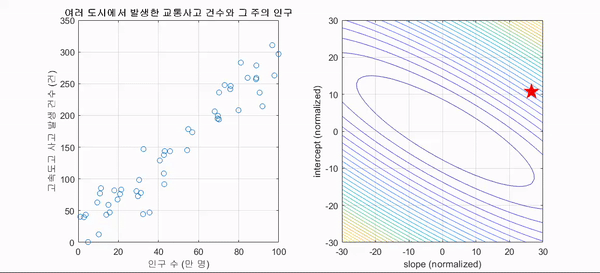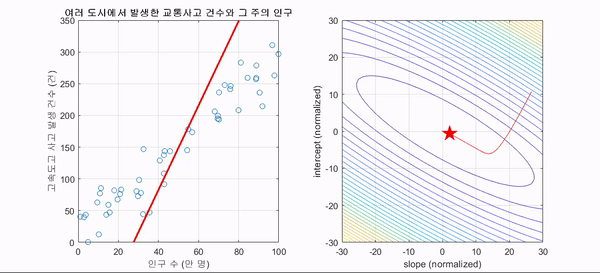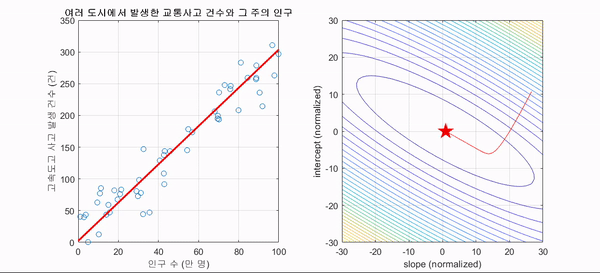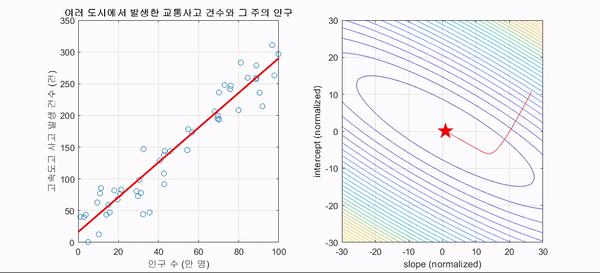
Objective Function (목적 함수)

모든 모델(함수)에 대하여 우리가 가장 일반적으로 사용하는 용어로서 최댓값, 최솟값을 구하는 함수

→ 학습시키는 모델(함수)에 대해서 최적화(Optimization) 시키고자 하는 모든 함수들.

최대화(maximization) : 이윤, 점수(score) 등
최소화(minimization) : 비용(cost), 손실(loss), 에러(error) 등

손실 함수는 목적 함수의 한 유형인 비용 함수의 일부.

Activation Function (활성화 함수)

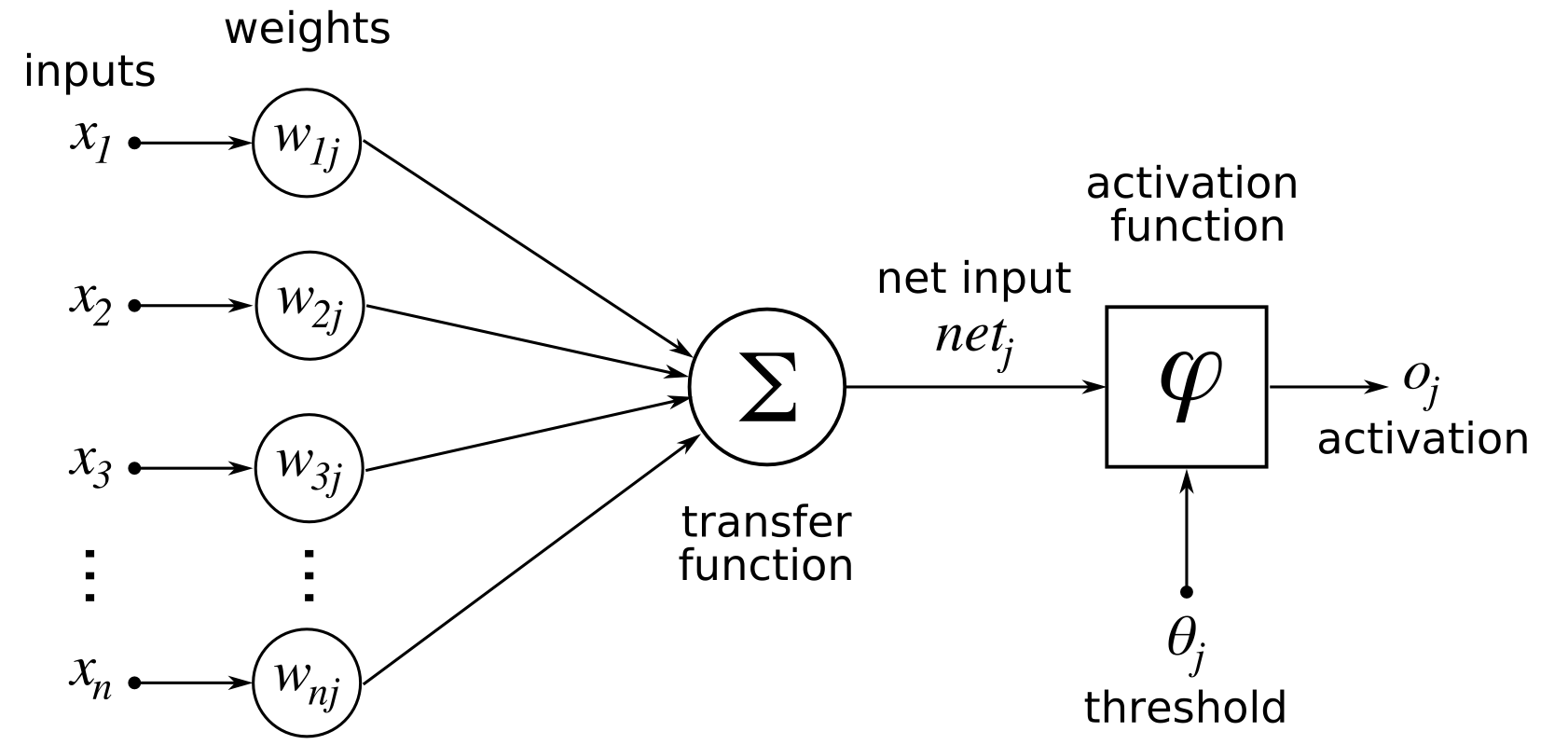
이전 레이어들로부터 온 값들, 즉 입력 신호의 총합을 출력 신호로 변환하는 함수이다.

Activation이라는 단어 자체에서 알 수 있듯이, 입력 신호의 총합이 다음 레이어의 활성화를 일으킬 지 말 지를 결정한다.

→ 좀 더 알기 쉽게 비유를 해보자면, 학창 시절 과학 시간에 봤었던 전기 파트의 회로도 중, 스위치의 역할을 한다고 보면 될 것 같다.

Loss Function vs Cost Function

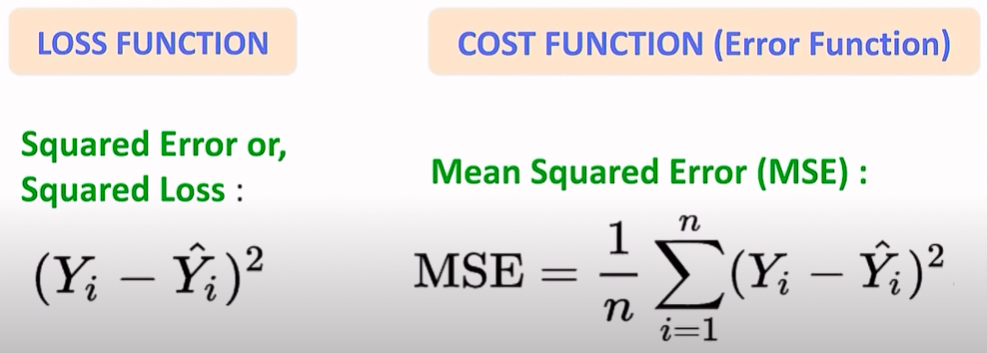
학습 진행 중의 데이터 하나하나의 차이는 loss,
학습 완료 후의 모든 데이터의 loss들의 평균을 cost.

순간순간의 loss를 판단할 땐 loss function을,
학습이 완료된 후에는 cost function을 확인.

ref) https://box-world.tistory.com/6
https://stats.stackexchange.com/questions/179026/objective-function-cost-function-loss-function-are-they-the-same-thing
https://www.youtube.com/watch?v=N1pevBt2Nfo
https://www.youtube.com/watch?v=KoC99FDHQpQ
https://darkpgmr.tistory.com/149

https://heytech.tistory.com/380

https://brunch.co.kr/@namujini/23