[KMooc] Classification - KNN

티나(Tina)·2022년 11월 21일

kmooc

목록 보기

3/6

최근접 이웃법 새로운 데이터를 입력 받았을 때 가장 가까이 있는 것이 무엇이냐를 중심으로 새로운 데이터의 종류를 정해주는 알고리즘이다.

여기서 K 는 이웃의 숫자다. 보편적으로 K 값은 홀수로 지정한다. K는 하이퍼파라메터로 사용자가 지정해 줄 수 있다.
KNN은 새로 들어온 데이터가, K 개의 주변 관측치에서 가장 많이 분포해 있는 클래스로 속한다고 분류하는 방식이다.

KNN은 분류를 거리에 기반을 하기 때문에 Distance-based model 이라고 하고,
개별 instance들에 대해서 특성들을 공유할 것이라는 가정을 기반에 두기 때문에 instance-based learning이라고 표현한다.

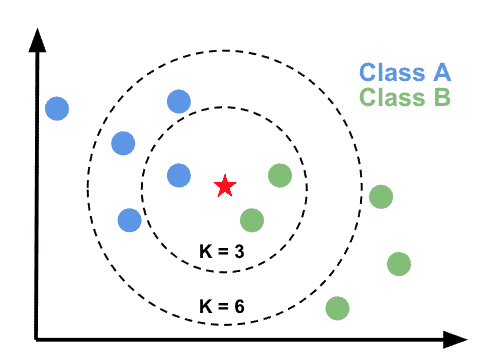
K 에 따라서 분류 결과가 달라진다.

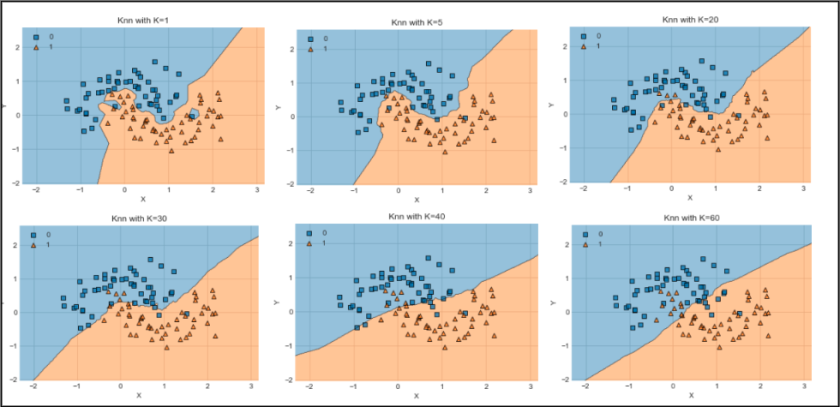
K 가 크면 Underfitting, K 가 작으면 Overfitting
- K가 크면 클수록 주위에 더 많은 사례들을 보기 때문에 좀 더 단순한 분류 경계선, 단순화된 모형을 보여주고,
- K가 작으면 작을수록 미세한 변동에 영향을 받아서 분류하는 결과가 되기 때문에 모델의 Complexity가 큰 분류가 된다.

지도 학습은, 예측함수를 제시해주는데 KNN은 함수형테가 없고 관측치들간의 거리를 계산해서 알고리즘에 적용하는 모델이다. 그래서 Lazy Learning 알고리즘이라고 부른다.
- 예를들면, Linear Regression의 경우 training 으로 예측함수가 완성?이 되고 데이터가 오면 예측된 선형 함수에 맞게 결과물이 바로 나온다.
- 반면 KNN은 학습이 따로 없고, 데이터가 들어오면 training 데이터와의 거리를 구하고 그에 맞게 결과가 나온다.
KNN 은 훈련 데이터가 많다면 꽤 좋은 성능을 낸다.
but, 차원이 증가하는 경우 성능이 크게 저하된다!!! 차원이 증가하면 점들 사이 거리가 증가하기 때문에 한차원에서는 충분 했던 데이터도 차원이 늘어나면 데이터가 부족하게 된다.
- 이 경우 데이터의 갯수를 늘리거나
- 차원을 축소하여 해결한다.
거리기반 알고리즘이기 때문에 변수값 scaling 이 필요하다. 변수들의 값을 재조정해주어야 변수의 중요도를 고르게 해설 할 수 있다.

KNN 거리를 구하는 방식

유클리드 (Euclidean Distance) : 기하학적 최단 거리(직선 거리)
$d(A,B)= \sqrt{(x2−x1) 2 +(y2−y1) 2}$
맨하탄 (Manhattan Distance) : 격자 형태의 공간에서의 거리
$d(A,B)=∣x1−x2∣+∣y1−y2∣$
민코프스키 (Minkowski Distance) : 유클리드 거리와 맨해튼 거리를 일반화한 것

(\displaystyle\sum_{i=1}^n ∣x_i −y_i ∣^p ) ^{1/p}

p = 1 인 경우 맨하탄 거리가 되고,
p = 2 인 경우 유클리디안 거리,
p = ${\infin}$ 인 경우는 체비쇼프 거리가 됩니다.

열심히 사는 중