Today I Learned
오늘 배운 내용은 경사하강법!
경사하강법
최적화 알고리즘 중 하나로, 함수의 최소값(or 최대값)을 찾기 위해 반복적으로 함수의 기울기를 따라 내려가는 방법이다.
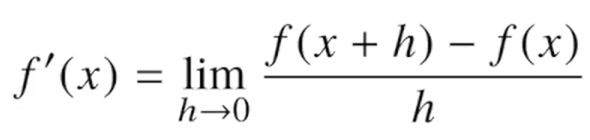
미분(Differentiation)
변수의 움직임에 따른 함수값의 변화를 측정하기위한 도구, 변화율, 접선의 기울기
- python에선 sympy 라이브러리의 diff를 가지고 미분을 쉽게 계산할 수 있다.
import sympy as sp
# 변수와 함수 정의
x = sp.symbols('x')
f = x**3 + 2*x**2 + 3*x + 4
# 함수 f를 x에 대해 미분
f_prime = sp.diff(f, x)
# 결과 출력
print("f'(x) =", f_prime)미분값을 활용한 경사하강(상승)법

-
미분값을 알면 어느 방향으로 점을 움직여야 함수값이 증가/감소하는 지 알 수 있다.
증가시키려면 미분값을 더하고, 감소시키려면 미분값을 빼면 된다. -
이렇듯 미분값을 더해주면서 함수값을 점차 상승시키는 방법을
경사상승법(gradient ascent)이라 하며 극대값의 위치를 구할 때 사용한다. -
반대로 미분값을 빼주면서 함수값을 점차 감소시키는 방법을
경사하강법(gradient descent)이라 하며 극소값의 위치를 구할 때 사용한다. -
두 방법은 모두 극값에 도달하면 미분값이 0이기 때문에 움직임을 멈춘다.
-
컴퓨터로 계산할 때 미분값이 0이되는 것은 거의 불가능하므로
eps(알고리즘 종료 조건)보다 작을때 종료되도록 설정해두어야 한다. -
learning rate(lr, 학습률)을 통해 경사하강법 알고리즘의 속도를 조절할 수 있다.
편미분(partial differentiation)
다변수 함수에서 한 변수를 기준으로 다른 변수들을 고정시킨 후에 해당 변수에 대해 미분하는 과정
-
변수가 벡터인 경우, 즉 벡터가 입력인 다변수 함수의 경우 편미분을 사용한다.
-
특정 방향의 좌표축으로 이동하는 형식으로 미분을 진행하는 데 이를 편미분이라 한다.
-
ei는 i번째 값만 1이고 나머지는 0인 단위벡터를 의미한다.
-
sympy를 이용한 편미분 방법
import sympy as sp
# 변수 정의
x, y = sp.symbols('x y')
# 함수 정의
f = x**2 + x*y + y**2
# x에 대한 편미분
partial_x = sp.diff(f, x)
print("f(x, y)를 x에 대해 편미분한 결과:", partial_x)
# y에 대한 편미분
partial_y = sp.diff(f, y)
print("f(x, y)를 y에 대해 편미분한 결과:", partial_y)
Gradient 벡터
다변수 함수의 편미분으로 이루어진 벡터
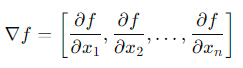
-
각 변수별로 편미분을 계산한 그레디언트(gradient) 벡터를 경사하강/상승법에 사용할 수 있다.
-
수식의 역삼각형을 nabla라고 한다.
-
다변수 함수의 경우, 여러 변수에 대한 도함수가 있으므로, 그레디언트를 사용하여 이러한 모든 도함수의 값을 하나의 벡터로 표현할 수 있다.
-
그레디언트 벡터를 사용할 경우 절대값대신 노름을 계산해 종료 조건(eps)을 설정한다.
본 포스트의 학습 내용은 부스트클래스 <AI 엔지니어 기초 다지기 : 부스트캠프 AI Tech 준비과정> 강의 내용을 바탕으로 작성되었습니다.
