Today I Learned

오늘 공부한 내용은 뉴럴네트워크와 MLP!

뉴럴 네트워크

인간의 두뇌에서 영감을 얻은 방식으로 데이터를 처리하도록 컴퓨터를 가르치는 인공 지능 방식

• 인간의 두뇌와 비슷한 계층 구조로 상호 연결된 노드(or 뉴런)을 사용하는 딥 러닝의 유형

• 기술이 점차 발전하면서 인간의 뇌를 모방하는 방식과는 많이 멀어졌다.

• 수학적 정의

  Neural networks are function approximators that stack affine transformations followed by nonlinear transformations.
  입력 데이터에 대해 선형 변환을 적용하고 이어서 비선형 변환을 쌓아서 복잡한 함수를 근사화하는 것

MLP(Multilayer Perceptron)

• 가장 간단한 구조는 Linear 구조(선형회귀)
  

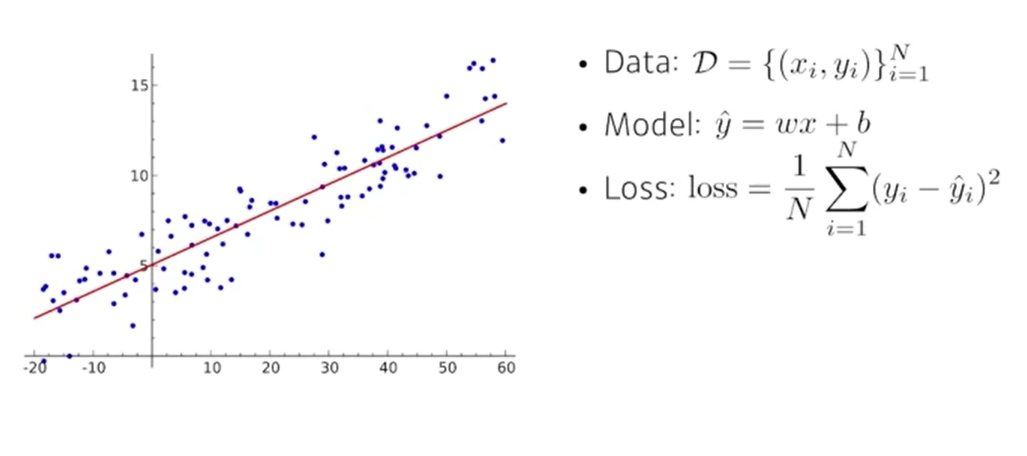
• Linear로만 해결이 안되면 행렬을 사용
  (Weight, bias)로 x를 y로 보낸다.
  

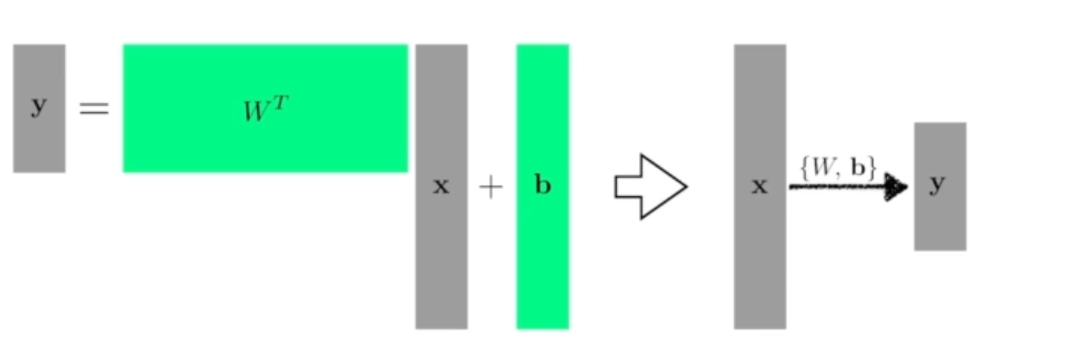
• 딥러닝은 결국 shallow하지 않고 깊게 network를 쌓겠다는 것.
  단순히 선형결합만을 여러개 쌓기만 하지 않고 nonlinear transform을 추가
  

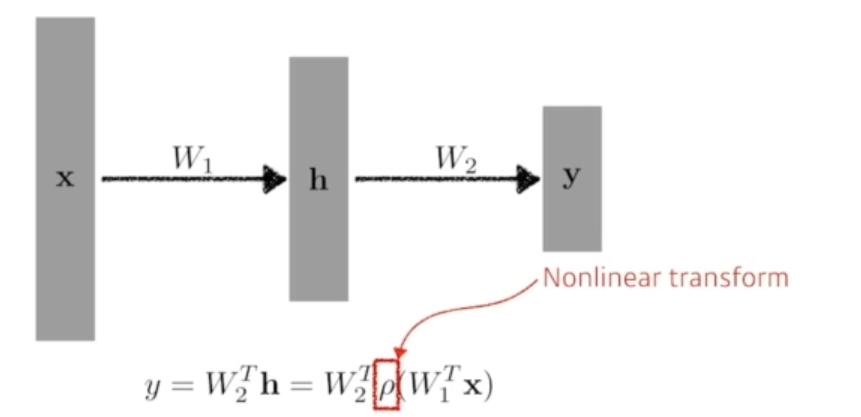
• Activation Functions(nonlinear transform)
  ReLu, Sigmoid, Hyperbolic Tangent 등
  

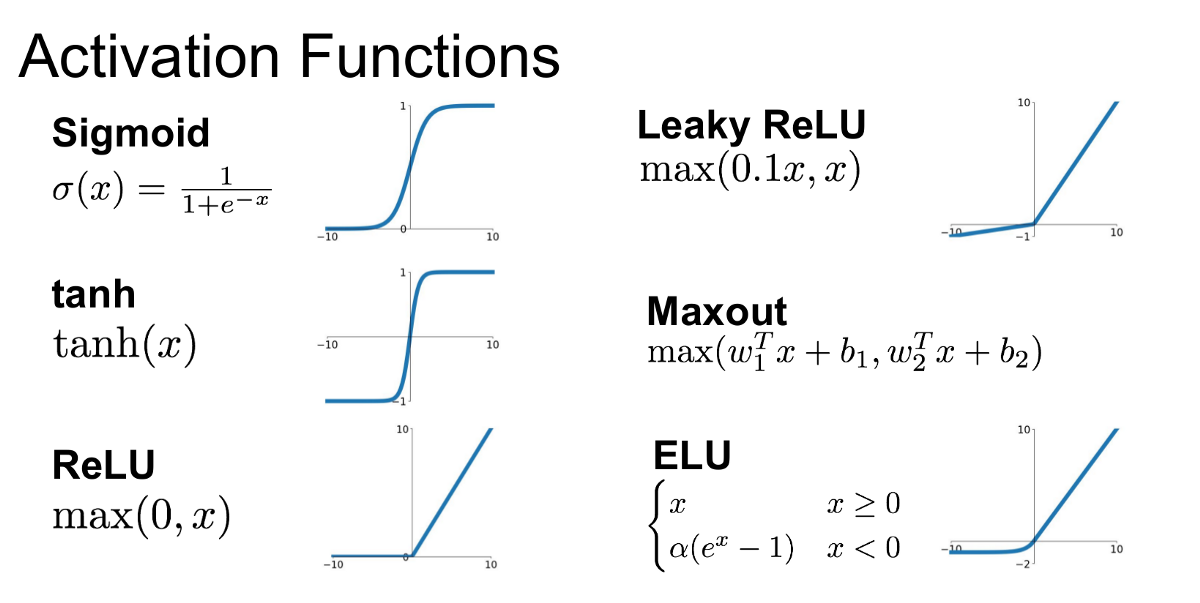
• 계속 network를 쌓을 수 있다
  

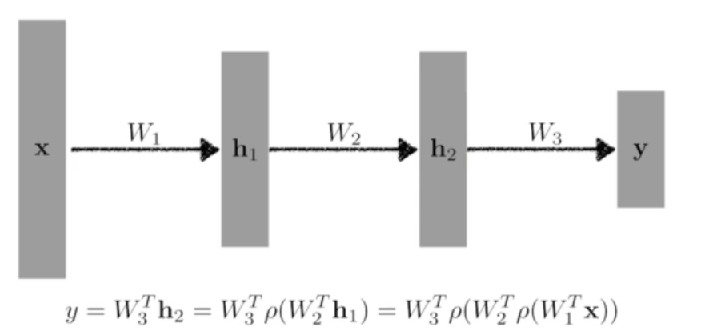
Loss Fucntion

MSE vs MAE VS RMSE

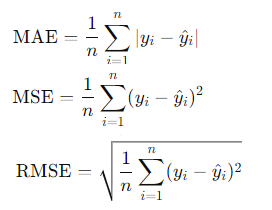
MSE (Mean Squared Error): 에러의 제곱을 평균한 값으로, 큰 에러에 대해 더 큰 페널티를 부여하고, 이상치에 민감하다.
RMSE (Root Mean Squared Error): MSE의 제곱근을 취한 값으로, 실제 단위로 오차를 표현한다. MSE와 마찬가지로 큰 에러에 민감하다.
MAE (Mean Absolute Error): 에러의 절대값을 평균한 값으로, 이상치에 덜 민감하다.

회귀문제에서 사용하는 손실함수 중 MSE와 MAE의 차이는 학습데이터에 에러가 껴있을 때 그 데이터에 맞추려다가 전반적인 모델이 전부 망가질 수 있는데, MSE는 처리되지 않은 이상치를 민감하게 학습해 불안해질 가능성이 있다.

• MAE는 이상치에 대해 강건(robust)하기 때문에 이상치에 영향을 덜 받는다.

• RMSE는 MSE 보다 이상치에 대해 상대적으로 둔감하다. RMSE는 각 오차가 다른 가중치를 갖는 반면, MAE는 오차에 동일한 가중치를 갖는 차이점이 있다.

CE(Cross-Entropy)

분류문제에서 사용하는 손실함수

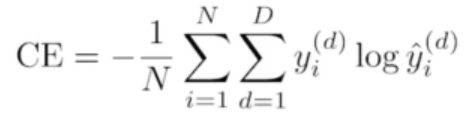
• 두 확률 분포의 차이를 구하기 위해서 사용된다.

본 포스트의 학습 내용은 부스트클래스 <AI 엔지니어 기초 다지기 : 부스트캠프 AI Tech 준비과정> 강의 내용을 바탕으로 작성되었습니다.