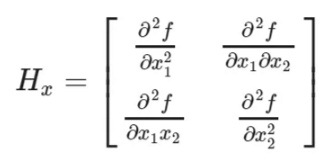이 포스팅은 A Comparative Analysis of SIFT, SURF, KAZE, AKAZE, ORB, and BRISK(2018) 논문을 참고하여, SIFT를 비롯한 Feature Descriptor들에 대한 비교를 정리한 글이다.
stitching project를 하다 보니 특징 디스크립터에 대한 이해가 필요해져서 관련 포스팅도 여러개 찾아보고, 직접 opencv 모듈로 구현해서 적용해 보았지만 논문 보면서 직접 정리하는 것이 이해에 많은 도움이 되기 때문에 !
먼저, feature matching에 필요한 feature descriptors(특징 디스크립터)들을 설명하기 앞서, 이 특징 디스크립터들이 왜 필요한 지 간략하게 알아보자.
영상 정합(Image Registration)
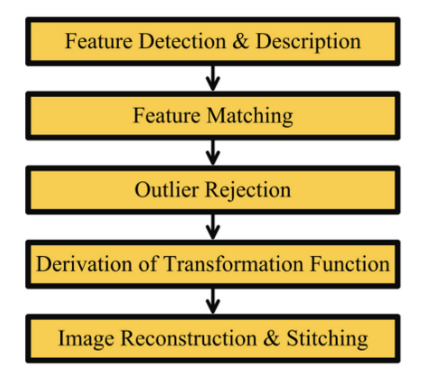
- 영상 정합(Image Registration)이란?
하나의 장면이나 대상을 다른 시간이나 관점에서 촬영할 경우, 서로 다른 좌표계의 영상이 얻어지게 된다. 이러한 좌표계들의 영상을 변형하여 하나의 좌표계에 나타내는 처리 기법이다.
영상 정합은 위 flowchart와 같이 5단계의 과정을 거치는데, feature-based 영상 정합은 feature detector-descriptor의 선택에 따라 연산 속도와 정확도가 좌우된다. 따라서, feature matching application에서 feature detector-descriptor의 선택이 매우 중요하다.
특징 디스크립터(Feature Descriptors)
특징 디스크립터는 string-based descriptor와 binary descriptor로 나뉜다.
string based에는 SIFT, SURF, KAZE 등이 있으며, binary에는 AKAZE, ORB, BRISK 등이 있다.
string-based descriptors(SIFT, SURF, KAZE, etc.)
L1 Norm 또는 L2 Norm을 사용하여 feature matching을 수행한다.
- SIFT(Scale Invariant Feature Transform) (2004)
가장 잘 알려진 feature detection-description 알고리즘이다.
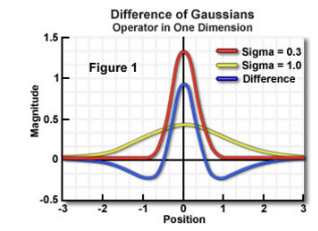
DoG(Difference-of-Gaussian) operator를 기반으로 한다.대상 이미지의 다양한 척도에서 DoG를 사용하여 국소 최댓값(local maxima)들을 탐색하는 과정을 통해 특징점이 검출된다. 검출된 각 특징을 둘러 싼 16x16 크기의 neighborhood를 추출하고, 총 128개의 bin 값을 렌더링하여 해당 구역을 서브 블록으로 나눈다. SIFT는 image rotation, scale, limited affine variations에 매우 invariant 하지만, 연산 비용이 높다는 단점이 있다.
- DoG (Difference of Gaussians)
DoG는 가우시안 블러를 적용한 이미지와 가우시안 블러가 약하게 적용된 이미지의 차이를 구하는 feature enhancement algorithm이다.
- SURF (Speeded Up Robust Features) (2008)
SIFT와 마찬가지로 가우시안 척도의 이미지 공간 분석을 기반으로 한다.
SURF detector는
Hessian Matrix(헤세 행렬)의 determinant를 기반으로 하고, integral image를 사용하여 feature detection 속도를 향상시킨다.SURF는 64 bin descriptor를 사용하여 특정 neighborhood 내의 Haar wavelet response의 분포와 각각의 검출 특징을 설명한다.
- Hessian Matrix(헤세 행렬)
Hessian은 함수의 곡률(curvature) 특성을 나타내는 행렬로, 극소점(local minimum), 극대점(local maximum), 안장점(saddle point, 보는 방향에 따라서 극대, 극소가 바뀌는 점)을 구하는 데 사용될 수 있다.
어떤 함수의 critical point(일차미분이 0이 되는 되는 점)에서 계산한 Hessian 행렬의 모든 고유값(eigenvalue)이 양수(positive)이면 해당 지점에서 함수는 극소, 음수이면 극대, 음의 고유값과 양의 고유값을 모두 가지면 안장점이 된다.Hessian 행렬의 고유벡터(eigenvector)는 함수의 곡률이 큰 방향벡터를 나타내고 고유값(eigenvalue)은 해당 고유벡터(eigenvector) 방향으로의 함수의 곡률(curvature, 이차미분값)을 나타낸다.
- Haar Wavelet Transform(웨이블릿 변환)
Haar wavelet은 Haar transform은 재조정된 정사각형 모양 함수의 시퀀스로, 타깃 함수를 일정 간격에서 orthonormal basis(정규직교)로 나타낼 수 있다. 가장 단순한 wavelet transform(웨이블릿 변환) 방식이다. Harr matrix를 통해 변환하며, 이미지 압축에 많이 사용된다.
- KAZE (2012)
KAZE는 비선형 확산 필터링(non-linear diffusion filtering)을 통해 비선형 척도 공간을 이용한다.
다음은 비선형 확산 필터링의 예시(이미지)이다.
KAZE는 특징점에 극소적으로 adaptive한 이미지에 블러를 하고, 이에 따라 잡음을 감소시킴과 동시에 대상 이미지의 바운더리 영역을 얻는다. KAZE detector는 다중 척도에서 연산되는 Hessian Matrix의 scaled normalized determinant를 기반으로 한다.detector response의 최댓값은 window를 이동시켜 특징점으로 선택된다. Feature description은 각각의 탐지된 특징을 둘러 싼 circular neighborhood에서 dominant orientation을 찾아냄으로써 rotation invariant하게 된다.
KAZE는 rotation, scale, limited affine에 invariant하며, 컴퓨팅 연산 시간을 적절히 증가시킬 경우 다양한 척도에서 더욱 distinctive하게 된다.
binary descriptors (AKAZE, ORB, BRISK, etc.)
Hamming distance를 사용하여 feature matching을 수행한다.
- AKAZE(Accelerated-KAZE) (2013)
KAZE와 같이 non-linear diffusion filtering을 기반으로 하지만, 비선형 척도 공간을
Fast Explicit Diffusion(FED)라 불리는 연산 효율적 프레임워크를 사용하여 구축한다.AKAZE detector는
Hessian Matrix의 determinant에 기반하고,scharr filter를 사용하여 rotation invariance quality를 향상시켰다. 공간적 극소에서 detector response의 최댓값이 특징점으로 선택된다. AKAZE descriptor는 매우 효율적인 알고리즘인Modified Local Difference Binary(MLDB)알고리즘에 기반한다. AKAZE는 scale, rotation, limited affine에 invariant하고, 비선형 척도공간으로 인해 다양한 척도에서 더 dsitinctive하게 된다.
- ORB(Oriented FAST and Rotated BRIEF) (2011)
ORB는 변형된
FAST(Features from Accelerated Segment Test)detection과 direction-normalizedBRIEF(Binary Robust Independent Elementary Features)description 방법론을 혼합한 알고리즘이다.FAST corners는 척도 피라미드의 각 층에서 탐지되며, 탐지된 지점의 cornerness는 최고 퀄리티의 point를 필터링하기 위해 Harris Corner를 사용하여 검증한다.
BRIEF description method는 rotation에 매우 안정적이지 못하고, 따라서 BRIEF의 변형된 버전을 사용했다.
ORB는 scale, rotation, limited affine changes에 invariant하다.
- BRISK(Binary Robust Invariant Scalable Keypoints) (2011)
BRISK는
AGAST알고리즘을 사용하여 corner를 탐지하고, 척도 공간 피라미드에서 최댓값을 탐색하는 동안 FAST corner score로 탐지된 코너들을 필터링한다.BRISK description은 rotation invariance를 얻기 위해 각 특징의 characteristic direction을 확인하는 과정에 기반한다. BRISK는 scale, rotation, limited affine changes에 invariant하다.
feature description 알고리즘 비교
- 많은 양의 피쳐 검출(ability to detect high quantity of features)
ORB>BRISK>SURF>SIFT>AKAZE>KAZE
- 특징점 마다의 연산 효율성(computational efficiency of feature-detection-description per feature-point) ORB>ORB(1000)>BRISK>BRISK(1000)>SURF(64D)>SURF(128D)>AKAZE>SIFT>KAZE
- 특징점 마다의 매칭 효율성(efficient feature-matching per feature-point)
ORB(1000)>BRISK(1000)>AKAZE>KAZE>SURF(64D)>ORB>BRISK>SIFT>SURF(128D)
- 전체 매칭 속도(speed of total image matching)
ORB(1000)>BRISK(1000)>AKAZE>KAZE>SURF(64D)>SIFT>ORB>BRISK>SURF(128D)
참고 논문에서는 속도나 연산 효율성 면에서는 ORB, BRISK가 좋다고 볼 수 있으며, 매칭의 정확도는 SIFT와 BRISK가 좋았다고 한다.
내 커스텀 데이터에 다양한 디스크립터로 stitching 연산을 적용해 보았을 때, 확실히 ORB가 속도 면에서 좋은데 정확도가 떨어져서 confidence threshold를 낮춰 사용하는 것이 좋아 보인다.
꼭 실험 결과가 데이터에 맞지 않을 수 있지만(맞지 않는것 같기도...), 알고리즘 원리에 대해 간단히 알아보고, 정리해서 비교해 보는 좋은 시간이 되었다.