outlier detection(이상값 탐지) 구현

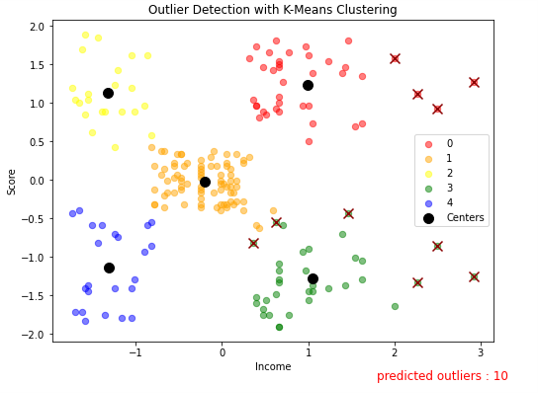
clustering(군집화)과 classification(분류) 기법으로 outlier detection을 구현해 보자

✅ 개념 정리(들어가기 전)

---

데이터 이상값(Data outlier)

• 데이터 이상값은 관측된 데이터 범위에서 많이 벗어난 아주 작은 값, 또는 아주 큰 값
• 입력 오류, 데이터 처리 오류 등의 이유로 특정 범위에서 벗어난 데이터값

---

이상값 발생 원인

(1) 표본 추출 오류(sampling error)

• 표본 추출 오류는 데이터를 샘플링하는 과정(샘플링을 잘못 한 경우)에서 나타나는 오류

(2) 고의적인 이상값(intentional outlier)

• 자기 보고식 측정(self-reported measurement)에서 나타나는 오류

(3) 입력 오류(data entry error)

• 데이터를 수집, 기록, 입력 과정에서 발생하는 인간의 실수로 인한 오류
• 데이터 분포로 쉽게 탐지 가능

(4) 실험 오류(experimental error)

• 실험 조건이 동일하지 않은 경우

(5) 측정 오류(measurement error)

• 데이터 측정 과정에서 발생하는 오류

(6) 데이터 처리 오류(data preprocessing error)

• 데이터 마이닝에서, 여러 데이터에서 필요한 데이터를 추출하거나 조합해서 사용하는 경우 발생하는 오류

(7) 자연 오류(natural outlier)

• 인위적이 아닌, 자연스럽게 발생하는 이상값

---

이상값 검출 방법

1. 통계 기법을 이용한 데이터 이상값 검출

(1) ESD(Extreme Studentized Deviation)

• 평균(μ)으로부터 3 표준편차(σ) 떨어진 값을 이상값으로 판단하여 검출

(2) 기하평균

• 기하평균으로부터 2.5 표준편차(σ) 떨어진 값을 이상값으로 판단하여 검출

(3) 사분위수

• 제 1사분위, 제 3사분위를 기준으로 사분위간 범위(IQR)의 1.5배 한 값과 떨어진 위치를 이상값으로 판단하는 기법

(4) Z-score(표준화 점수)

• 평균이 μ이고 표준편차가 σ인 정규분포를 따르는 관측치들이 자료의 중심에서 얼마나 떨어져 있는지 파악하여 이상값을 검출

(5) Dixon Q-test(딕슨의 Q검정)

• 오름차순으로 정렬된 데이터에서 범위에 대한 관측치 간 차이에 대한 비율을 활용하여 이상값 여부 검정
• 데이터가 30개 미만일 경우 적절

(6) Grubbs T-test(그럽스의 T검정)

• 데이터가 정규분포를 만족하거나, 단변량 자료에서 이상값을 검정하는 방법

(7) Chi-square test(카이제곱 검정)

• 데이터가 정규분포를 만족하나, 자료 수가 적은 경우 이상값을 검정하는 방법

(8) Mahalanobis distance(마할라노비스 거리)

• 데이터의 분포를 고려한 거리 측도로, 관측치가 평균으로부터 벗어난 정도를 측정
• 마할라노비스 거리를 이용하여 평균으로부터 벗어난 이상값을 검출
• 모든 변수 간 선형관계를 만족하고, 각 변수가 정규분포를 따르는 경우 적용 가능

---

2. 시각화를 이용한 데이터 이상값 검출

(1) 확률 밀도 함수

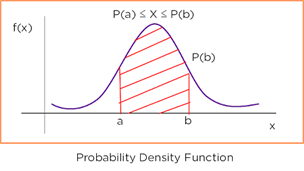
(2) 히스토그램

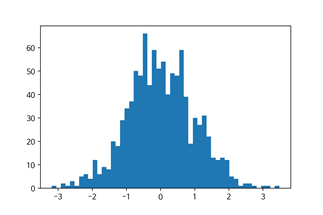
(3) 시계열 차트

---

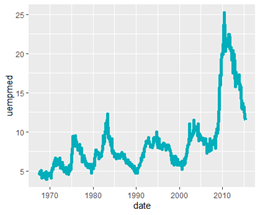
3. 군집 / 분류를 이용한 데이터 이상값 검출

(1) K-means Clustering(k-평균 군집화)

• 주어진 데이터를 K개의 클러스터로 묶는 군집화 방법으로, 각 클러스터와 거리 사이 분산을 최소화하는 군집 방법

(2) LOF(Local Outlier Factor)

• 관측치 주변의 밀도와 근접한 관측치 주변의 밀도의 상대적 비교를 통해 이상값 탐색
• LOF가 클수록 이상값 정도가 큼

(3) iForest(Isolation Forest)

• 관측치 사이 거리 또는 밀도에 의존하지 않고, 의사결정나무를 이용하여 이상값 탐지
• 분류 모형을 생성하여 모든 관측치를 고립시켜 나가며, 분할 횟수로 이상값 탐색
• 데이터 평균 관측치와 멀리 떨어진 관측치일수록 적은 횟수의 공간 분할을 통해 고립시킬 수 있음
• 적은 횟수로 잎 노드(leaf node)에 도달하는 관측치일수록 이상값 가능성이 큼

---

✅ 구현

여기서 구현해볼 이상값 탐지 방법론은 k-means clustering, LOF, iForest 3가지이다.
데이터는 케글의 Mall_customers dataset를 사용하였다.

(링크) Mall Customer Segmentation Data

---

1. outlier detection with K-means clustering

# 데이터 로드 및 확인
import pandas as pd
df = pd.read_csv('./data/Mall_Customers.csv')
df.head()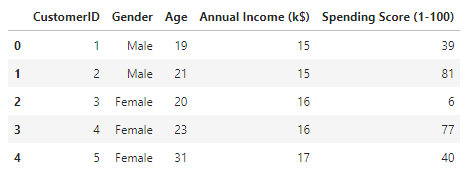

df = df.rename(columns={'Annual Income (k$)' : 'Income', 'Spending Score (1-100)' : 'Score' })

분석에 편하게 컬럼명을 변경해 주었다.

# standardize variables
from sklearn.preprocessing import StandardScaler 
scaler = StandardScaler()
df[['Income', 'Score']] = scaler.fit_transform(df[['Income', 'Score']])
df = df.loc[:, 'Income' :]
df.head()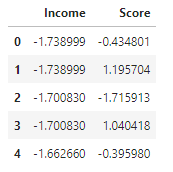

데이터 값을 스케일링 해준다. Income과 Score 값만 사용하기로 한다.

import matplotlib.pyplot as plt
plt.figure(figsize=(8, 6))
plt.scatter(df.Income, df.Score)
plt.xlabel('Income')
plt.ylabel('Score')
plt.show()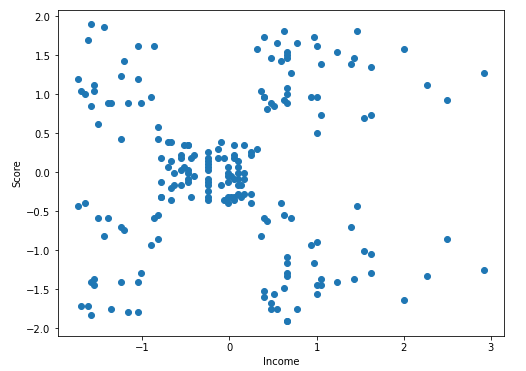

x축을 Income, y축을 Score로 해서 산점도를 그린 결과이다. 대충(??) 군집 수가 5개정도로 나뉠 것으로 보이므로 K=5로 군집화를 적용해 보겠다.

from sklearn.cluster import KMeans
km = KMeans(n_clusters=5)
model = km.fit(df)

import numpy as np
colors = ['red', 'orange', 'yellow', 'green', 'blue']

plt.figure(figsize=(8,6))
for i in range(np.max(model.labels_) + 1) :
    plt.scatter(df[model.labels_ == i].Income, 
               df[model.labels_==i].Score, label=i, c=colors[i], alpha=0.5, s=40)
plt.scatter(model.cluster_centers_[:, 0], model.cluster_centers_[:, 1], 
               label='Centers', c='black', s=100)
plt.title('K-Means clustering')
plt.xlabel('Income')
plt.ylabel('Score')
plt.legend()
plt.show()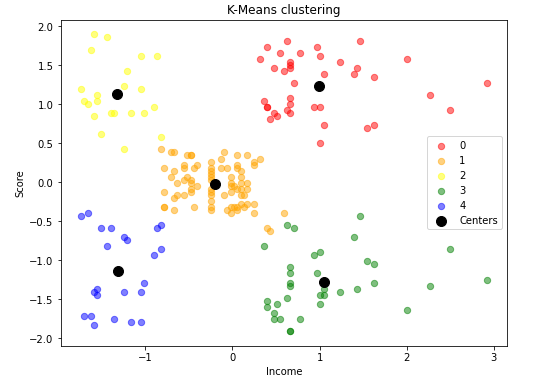

K=5로 군집화를 하고, 군집 결과와 각 군집의 중심점을 함께 시각화 해 본다.

# Outlier detection
# 각 센터에서 데이터의 거리를 계산
def distance_from_center(income, score, label) :
    center_income = model.cluster_centers_[label, 0]
    center_score = model.cluster_centers_[label, 1]
    dist = np.sqrt((income - center_income) ** 2 + (score - center_score))
    return np.round(dist, 3)

df['label'] = model.labels_
df['distance'] = distance_from_center(df.Income, df.Score, df.label)
df.head()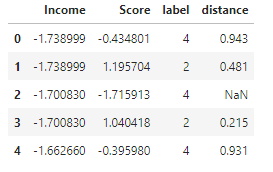

군집의 중심점에서 각 데이터까지의 거리를 계산한다.

# check most distant data
df.sort_values('distance', ascending=False).head(10)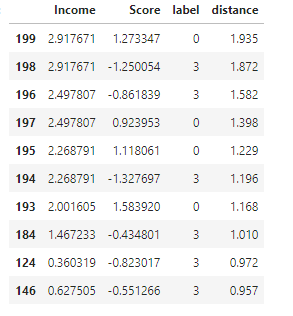

군집에서 가장 멀리 떨어진 데이터의 거리를 확인한다.

outlier_indexs = list(df.sort_values('distance', ascending=False).head(10).index)
outliers = df[df.index.isin(outlier_indexs)]
print(outliers)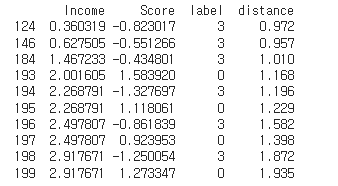

위에서처럼 10개의 가장 멀리 떨어진 데이터를 outlier로 판별해서 시각화를 해 보겠다.

# visualize outliers with scatter plot
plt.figure(figsize=(8, 6))
for i in range(np.max(model.labels_)+1) :
    plt.scatter(df[model.labels_==i].Income,
               df[model.labels_==i].Score, label=i, c=colors[i], alpha=0.5, s=40)
plt.scatter(outliers.Income, outliers.Score, c='darkred', s=100, marker='x')
plt.scatter(model.cluster_centers_[:, 0], model.cluster_centers_[:, 1], 
           label='Centers', c='black', s=100)
plt.title('Outlier Detection with K-Means Clustering')
plt.xlabel('Income')
plt.ylabel('Score')
plt.legend()

plt.text(1.8, -2.6, f'predicted outliers : {len(outliers)}',fontdict={'color':'red', 'size':12})
plt.show()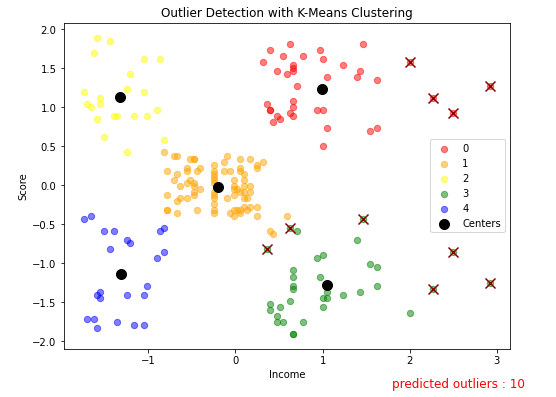

10개의 이상치에 대한 시각화 결과이다. 군집에서 멀리 떨어진 값들이 이상치(X)로 판별된 것을 볼 수 있다.

<참고 링크> Outlier Detection Using K-means Clustering In Python

---

2. Outlier Detection with LOF(local outlier factor)

from sklearn.neighbors import LocalOutlierFactor
lof = LocalOutlierFactor(n_neighbors=40, novelty=True, contamination=0.1)
# contamination : outlier percentage of train data
lof.fit(df.loc[:,:'Score'])

contamination은 학습 데이터의 몇%을 outlier로 지정할 것인지에 대한 파라미터이다.

# lof pred result : -1 outlier , 1 inlier
pred = lof.predict(df.loc[:, :'Score'])
n_errors = (pred != np.ones(200, dtype=int)).sum()
X_scores = lof.negative_outlier_factor_
radius = (X_scores.max() - X_scores) / (X_scores.max() - X_scores.min())

n = np.copy(X_scores)
n[n>sorted(X_scores)[n_errors-1]]=np.nan
n=np.round(n, 2)

plt.figure(figsize=(10, 8))
plt.title('Local Outlier Factor (LOF)')
plt.scatter(df.loc[:, 'Income'], df.loc[:, 'Score'], s=3.0, color='k', label='data points')

plt.scatter(df.loc[:, 'Income'], df.loc[:, 'Score'], s=1000 * radius,
           edgecolors='r', facecolors='none', label='outlier scores')
plt.axis('tight')
plt.xlabel('Income')
plt.ylabel('Score')
plt.legend(loc='lower right')

for i, text in enumerate(n) :
    if np.isnan(text) : 
        continue
    # annotation with outliers
    plt.annotate(text, (df.loc[i, 'Income'], df.loc[i, 'Score']))

plt.text(1.8, -2.6, f'predicted outliers : {n_errors}',fontdict={'color':'red', 'size':12})
plt.show()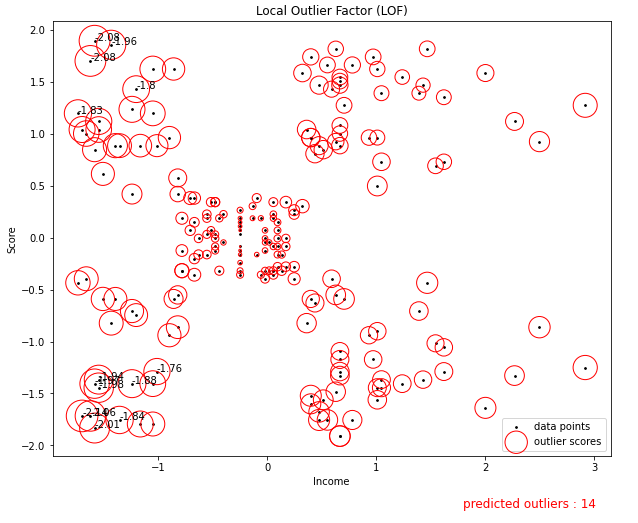

LOF값이 큰 순서대로 outlier로 판별된다.

<참고 링크>
1) Outlier detection with Local Outlier Factor (LOF)
2) Local Outlier Factor(LOF) 개인적 정리(with python)

---

3. Outlier Detection with iForest

from sklearn.ensemble import IsolationForest
iforest = IsolationForest(contamination=0.1)
iforest.fit(df.loc[:,:'Score'])
pred = iforest.predict(df.loc[:,:'Score'])
pred

-1로 보이는 값이 이상치, 1이 정상데이터로 판별된 것이다.

n_errors = (pred != np.ones(200, dtype=int)).sum()
n_errors

outlier_index = []
for i in range(len(pred)) :
    if pred[i] == -1 :
        outlier_index.append(i)

plt.figure(figsize=(8, 6))
plt.title('Outlier Detection with Isolation Forest (iForest)')
plt.scatter(df.Income, df.Score, label='data points')
plt.scatter(df.loc[outlier_index, 'Income'],df.loc[outlier_index, 'Score'], 
            marker='x', color='red', s=100, label='predicted outliers')
plt.xlabel('Income')
plt.ylabel('Score')
plt.text(1.8, -2.6, f'predicted outliers : {n_errors}',fontdict={'color':'red', 'size':12})
plt.legend(loc='center right')
plt.show()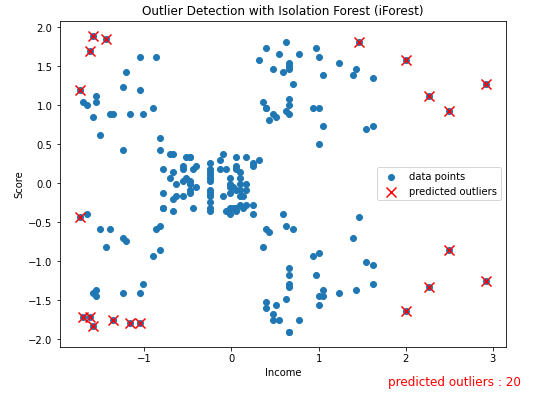

<참고 링크> Isolation forest을 이용한 이상탐지