lec 06-2
Contents
- what is Softmax?
- Softmax
- Cost function
- Cross-entropy cost function
- Cross-entropy 계산
- Logistic cost VS Cross entropy
ㅤ
ㅤ
ㅤ
ㅤ
what is Softmax?
Rogistic classfier에서 WX = y의 형태로 계산을 하면 어떤 입력값에 대한 세 개의 값을 낸다.
하지만 이 값은 1보타 클 수 있다.
따라서 위에서 나온 값들을 0에서 1까지의 값으로 바꾸어주는 것이 Softmax이다.
ㅤ
ㅤ
ㅤ
ㅤ
Softmax
엔개의 값을 Softmax에 넣게되면 바로 0부터 1사이의 값으로 수정되어 나온다.
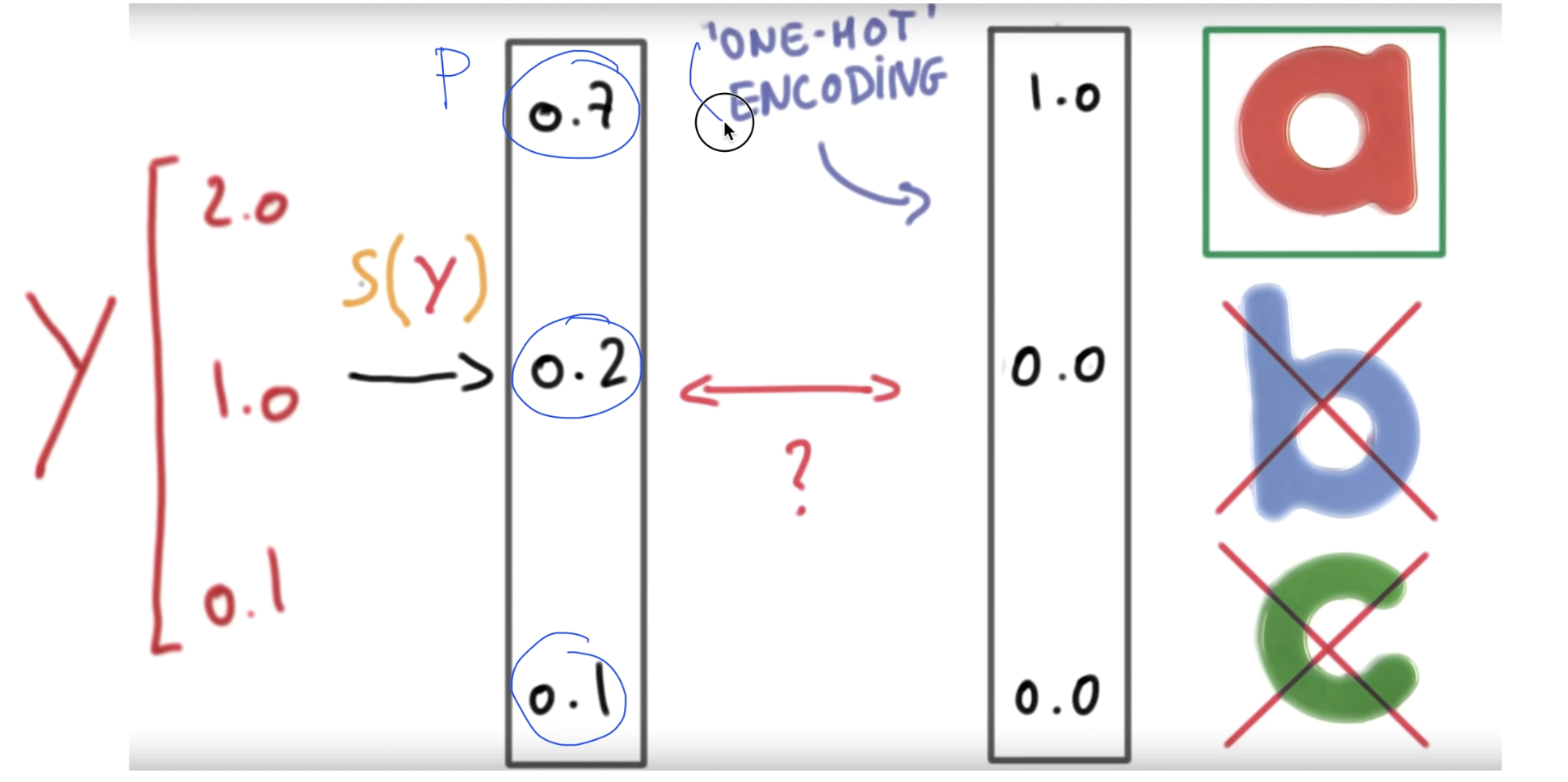
.특징
- 0 에서 1 사이다.
- 결과값의 총 헙아 1아다.
수정된 값을 각각의 확률로 볼 수 있는데, 이 확률을 모두 더하면 1이된다.
여러개의 결과 중 가장 높은 하나의 확률만 알고싶다면
one-hot-encoding 기법을 사용해 제일 큰 값을 1로, 나머지 값을 0으로 만들어줄 수 있다.
ㅤ
ㅤ
ㅤ
ㅤ
Cost function
Cross-entropy cost function
Cross-entropy cost function를 사용해 Softmax로 구한 예측과 정답의 차이를 구할 수 있다.
식은 아래와 같다.
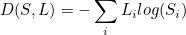
식에서
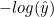
이 부분이 0과 1사이의 값을 가지는데, 그래프로 그리면 식이 가질 수 있는 범위는 파란색 선이다.
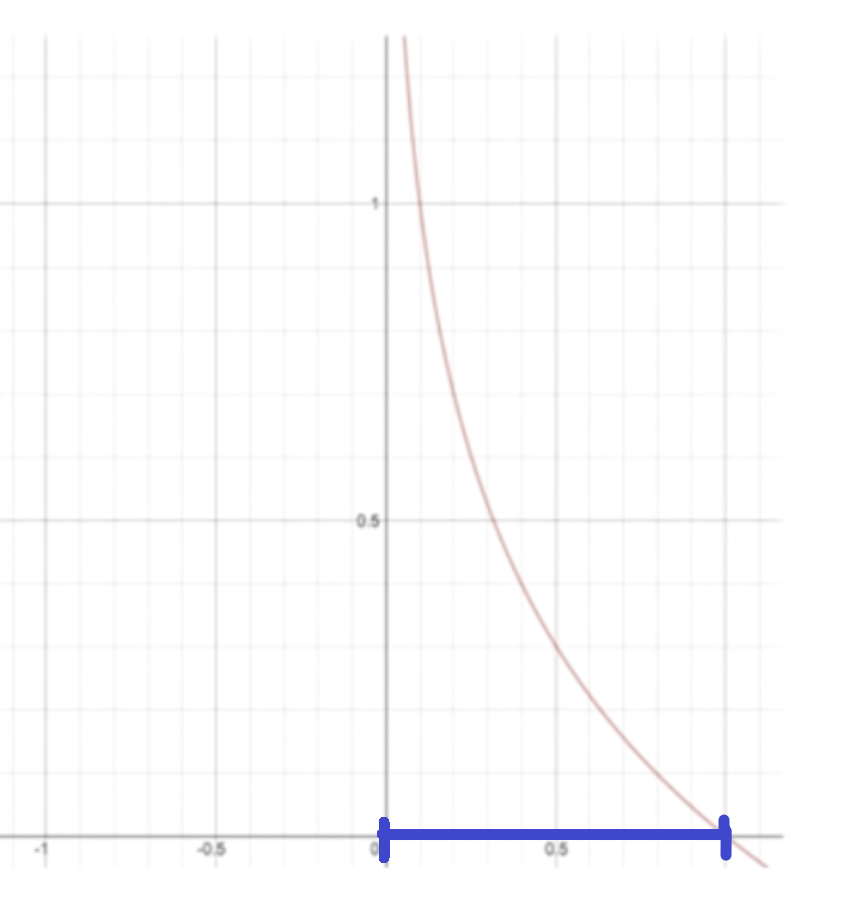
그렇다면 y의 값이 0일 때는 무한대에 가까워지고,
y의 값이 1이 될 경우, 0에 가까워지게된다.
우린 이 점을 활용해 계산할 것이다.
ㅤ
ㅤ
ㅤ
ㅤ
Cross-entropy 계산
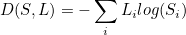
예를 들어,
정답 =
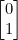
예측 =
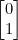
일 때,
위 식에서 정답은 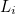
, 예측은 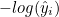
부분에 대입헤 곱한다.
따라서 결과는

이 된다.
이 값을 시그마에 넣어 계산하면 0이 된다.
ㅤ
ㅤ
반대로,
정답 =
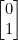
예측 =
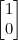
일 때는,
결괏값이

이 된다.
마찬가지로 이 값을 시그마에 넣어 전부 계산하면 최종적으로 결괏값은 ∞이 된다.
ㅤ
ㅤ
cost는 값이 작을 때 잘 계산된 것이고, 값이 클 때 잘못 계산된 것이기 때문에 cost가 잘 작동하는 것을 알 수 있다.
ㅤ
ㅤ
Logistic cost VS Cross entropy
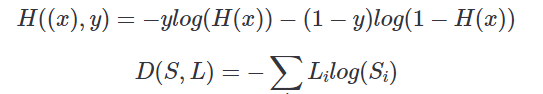
위 식에서 H((x), y)와 D(S, L) 부분이
앞은 예측값과, 뒤는 정답으로 같다.

