lec 10-1

Contents

• Activation function
  -9 hidden layers
• Tensorboard - 문제 원인 - Vanishing gradient - Sigmoid - 문제 해결
  ㅤ

ㅤ

ㅤ

ㅤ

Activation function

sigmoid 함수와 같은 것을 네트웨크에서는 Activation function이라고 지칭한다.

네트워크는 연결로 이루어져있는데, 하나의 값이 그 다음 값으로 전달될 때 어느 값 이상이면 activate, 아니면 deativate로 작용된다.

ㅤ

ㅤ

구현 시 소스코드
2단 네트워크

3단 네트워크 deep & wide

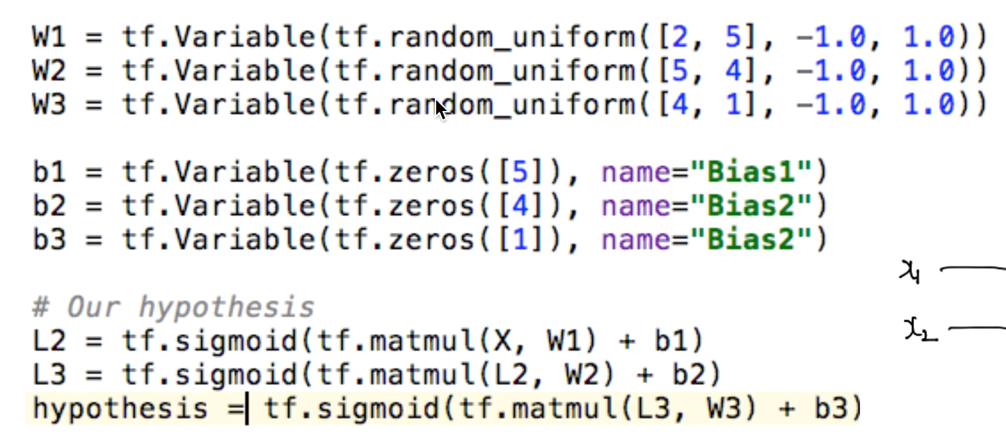
처음의 입력값은 2개 [2, 5]로, 마지막 출력값[4, 1]은 정해져있다.

hidden layer
특별한 의미 없이 input, output layer에서 안 보이기 때문에 붙은 이름이다.

ㅤ

ㅤ

9 hidden layers

구현 시 소스코드

체인을 계속해서 연결해주면 된다.
이것이 Deep Network이고, 계속 학습시키면 Depp Learning이 된다.

ㅤ

ㅤ

TensorBoard를 이용한 시각화

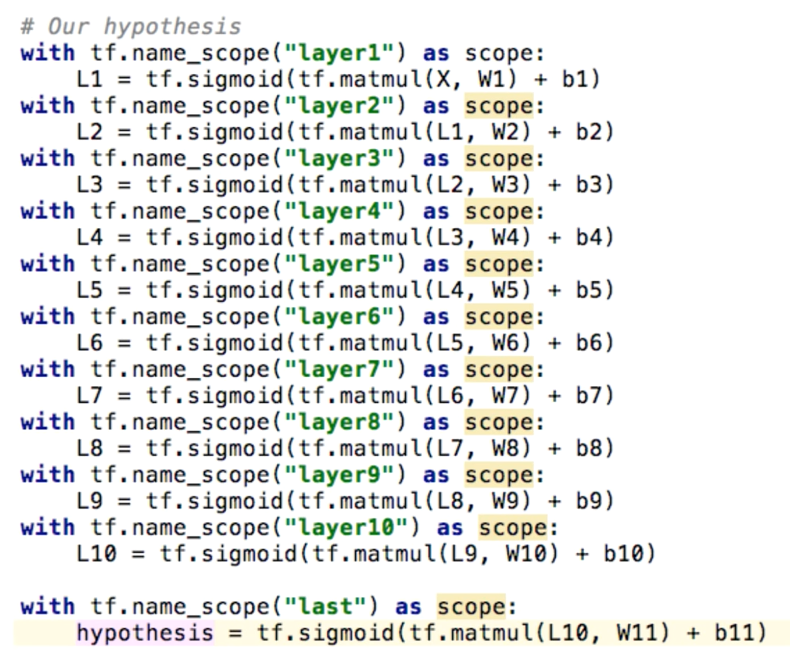
tf.name_scope를 통해 각각 이름을 붙여준다.
그리고 그 밑에 내가 원하는 layer들을 선언해준다.

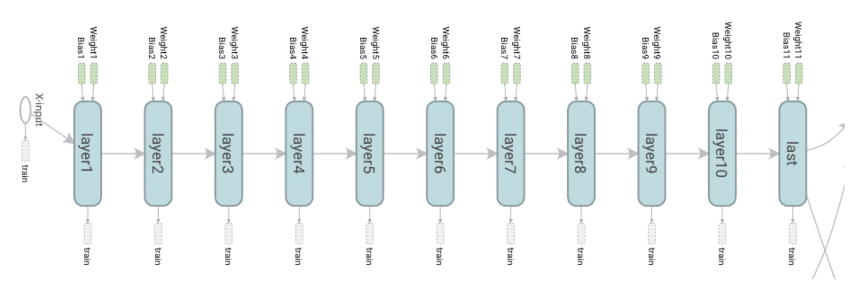
그림으로 보면 연결 상태, 각각의 W, b 등을 한 눈에 볼 수 있다.

ㅤ

ㅤ

실행
cost가 떨어지지 않고, accuracy도 0.5가 된다. = 1개 유닛한 것보다 나쁘게 나온다.

ㅤ

ㅤ

ㅤ

ㅤ

Tensorboard

ㅤ

ㅤ

문제 원인

Backpropagation 등장했을 때, 2, 3단 네트워크는 잘 학습 됐지만, 9단계처럼 많으면 학습이 되지 않는 문제가 있었다.

ㅤ

ㅤ

x가 최종 f에 미치는 영향을 알기 위하여 미분했었는데, 전체 미분을 하기 어려우니 하나 씩 미분하여 곱했었다.

뒤에서 전달된 값과 local의 미분 값을 chain rule로 곱했기 때문에, 소숫점 자리인 숫자들을 계속해서 곱해나가면 0.0001 \ 0.00001과 같이, 결국에는 0이 되어버리는 것이 문제가 된다.
결국 마지막 값은 사라지고, 이를 Vanishing gradient라고 부른다.

ㅤ

ㅤ

Vanishing gradient

앞쪽의 경사의 기울기는 존재하지만, 뒤로 갈수록 기울기가 점점 사라진다.

경사도가 사라진다. -> 학습하기 어렵다. -> x의 입력이 f에 영향을 끼치지 않는다. -> 예측이 안된다.

ㅤ

ㅤ

Sigmoid

sigmoid가 이러한 문제를 야기시킨다.
입력값이 주어지면 0에 가까운 값을 chain rule을 통해 계속 곱해 나가기 때문에, 출력값은 항상 작은 값이 나온다.

ㅤ

ㅤ

문제 해결

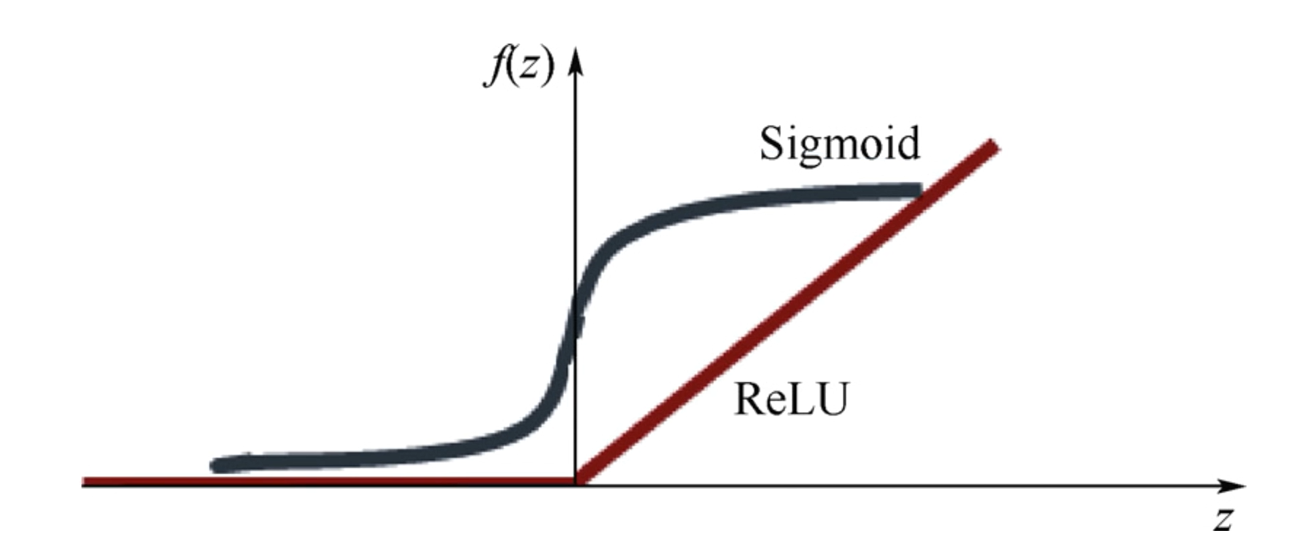
ReLU (Rectified Linear Unit)
Sigmoid를 넣는 대신에 ReLU를 넣는 것.
0보다 작을 경우 끝내고, 0보다 클 경우 값에 비례해서 계속한다.

ㅤ

ㅤ

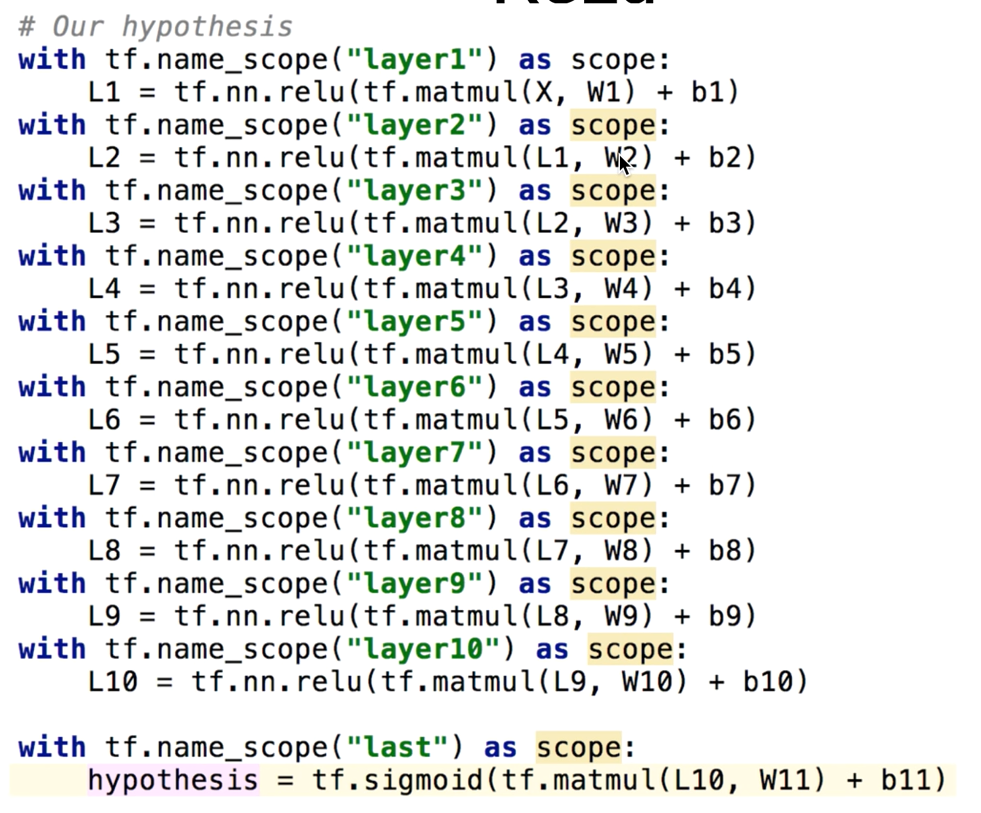
ReLU 적용
출력값이 0과 1 사이여야 하기 때문에, 마지막 단은 sigmoid를 사용한다.

ㅤ

ㅤ

ReLU의 변형

1. Leaky ReLU
   0 이하를 조금 살려준다.
   max(0.1x, x)

2. Maxout

3. ELU
   0 이하를 0으로 fix하지 말고 값을 바꿔준다.

4. tanh
   sigmoid의 단점을 보완해주고,
   sigmoid를 0의 중심으로 내려준다. (최소 -1, 최대 1)