그다지 전문적이지 않습니다...
서론
3D Reconstruction의 어려움
데이터의 부족
ImageNet부터 시작하여 정말 오랜 기간동안 양질의 데이터셋을 구축해온 2D 이미지와 달리 3D 모델에 대한 데이터셋은 턱없이 부족하다.
비정형화된 데이터
3D 정보를 표현하는 방법은 point cloud, voxel, polygon, vertex, LiDAR 스캔 데이터 등 정말 많은 형태로 존재하여 이들을 통합하는 것이 어렵다.
특히 3D 모델의 경우 같은 사물을 묘사하더라도 모델을 만든 사람마다 크게 달라질 수 있다.
이러한 이유로 인해 이미지를 다루는 분야와 달리 3D 관련 분야는 많이 발전하지 못한 상태였다.
NeRF (Neural Radiance Field)
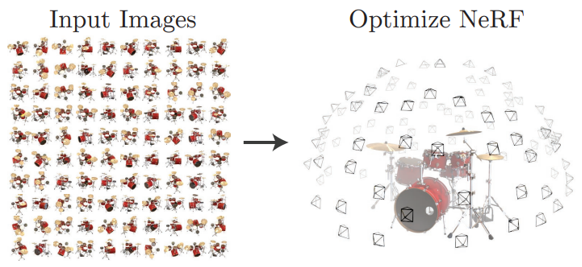

NeRF는 2020년 ECCV 2020에서 발표된 논문으로 여러 시점에서 오브젝트 또는 씬(Scene)을 찍은 이미지를 학습하여, 학습하지 않은 시점에서 봤을 때의 오브젝트/씬의 모습을 렌더링하는 모델이다.
즉 구하기 어려운 3D 데이터 없이 이미지 만으로 3D와 같이 연속된 시점을 묘사할 수 있게되어 3D 컴퓨터 비전 분야에서 지금까지도 NeRF를 기반으로 많은 연구가 이루어지고 있다.
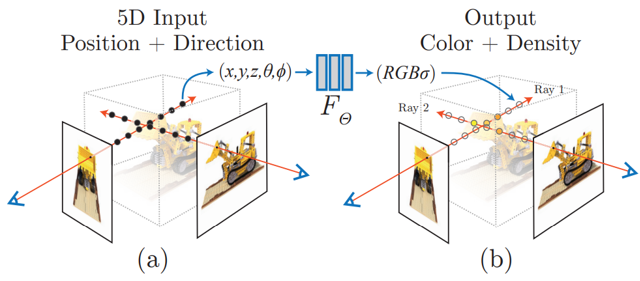
NeRF에 대해 아주아주 간략히 설명하면 Radience Field를 신경망으로 정의한 것을 뜻한다.
여기서 Radience Field는 임의의 위치 (x, y, z)와 시점 (θ, φ)을 Input으로 주었을 때, 해당 위치의 색상(RGB)과 밀도(σ, density)를 반환하는 함수를 뜻하는데
위의 사진과 같이 특정 시점에서 특정 픽셀을 향해 광선(Ray)을 쏘았을 때, 광선이 지나는 위치의 색상과 밀도를 Neural Radiance field를 통해 알아내어 해당 픽셀의 색상을 알아낼 수 있다.
NeRF의 한계
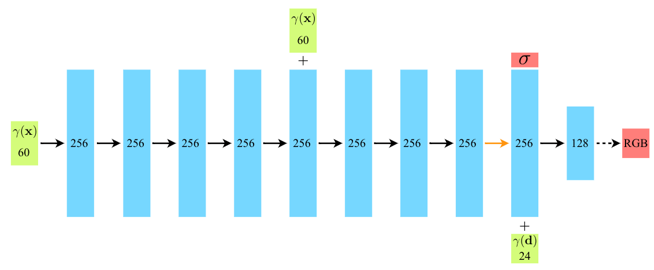
NeRF의 가장 큰 단점은 바로 성능이다.
그 이유는 크게 두가지로 꼽을 수 있다.
1. 새로운 이미지에 대해 매번 새로 학습해야 함
2. 새로운 시점을 생성할 때마다 위 그림과 같은 큰 규모의 MLP 연산이 필요
이로 인해 NeRF는 초기 학습시간이 오래걸리며, 시점이 바뀔 때마다 필요한 실시간 렌더링 성능이 떨어진다는 단점이 있다.
이러한 NeRF를 개선한 수많은 NeRF-based 모델이 나오고 있지만 근본적으로 퀄리티와 성능 사이의 trade-off 관계가 있다.
3DGS
3DGS는 새로운 시점 계산에 MLP가 필요없는 새로운 방법을 제시하였고, 그 결과 렌더링 성능이 획기적으로 개선되었다.
Overview
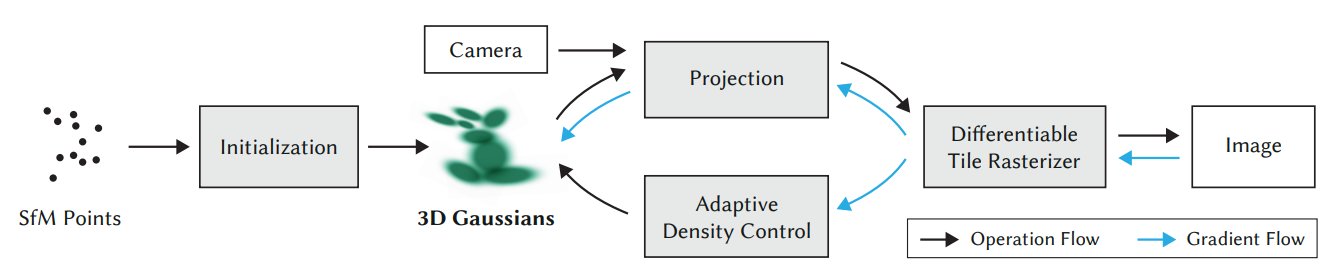
3DGS가 특정 시점에서의 2D 이미지를 렌더링 하는 방법은 다음과 같다.
- Scene을 나타내는 Point Cloud를 중심점으로 3D Gaussian을 생성
- 3D Gaussian 2D 이미지로 투영하여 렌더링 (여기에 Tile Rasterizer를 이용)
- 투영된 이미지와 Ground Truth를 비교해 Loss 계산
- Loss 값을 바탕으로 3D Gaussian을 업데이트. 이 때 Adaptive density control 기법을 사용
여기서 3DGS의 핵심 Contribution은 크게 세 가지가 있다.
- Differentible 3D Gaussian
- Adaptive density control
- Differentiable Tile Rasterizer
Differentible 3D Gaussian
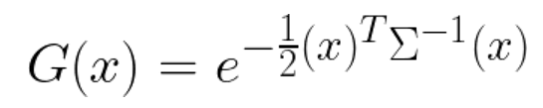
3D Gaussian은 중심점(x, y, z)을 평균으로 하고, 비등방성 공분산(anisotropic covariance) 분포로 정의 된다.
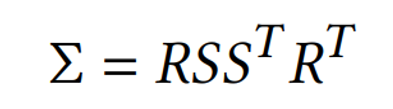
공분산 행렬은 크기(scale), 회전값(retation)을 기반으로 정의되며,
3차원 이므로 공분산은 (3x3)의 공분산 행렬이다.
각각의 Gaussian은 크기(scale), 회전 값을 갖고 있어 3D 공간에서 찌그러진 공(타원체)의 형태를 갖는다.
그리고 각 Gaussian은 색상값과 투명도값을 갖는다.
3DGS의 목표는 Geometry의 세세한 부분까지 묘사할 수 있도록 Gaussian의 수, 위치, 크기, 회전, 색상값, 투명도를 조절(가중치 업데이트)하는 것을 통해 정밀한 Scene을 묘사하는 Gaussian들을 화면에 흩뿌리는 것(Splatting )이다.

Adaptive density control
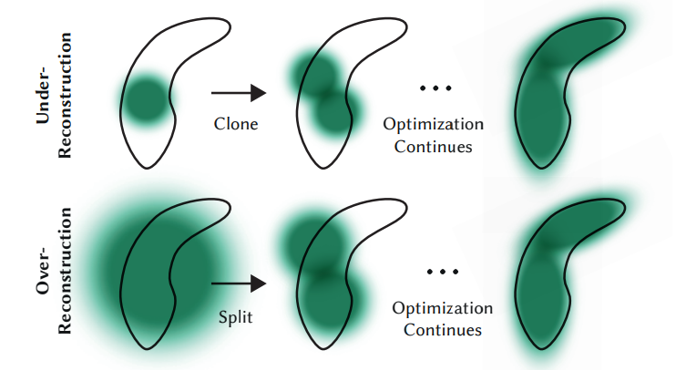
Adaptive density control은 씬을 정밀하게 표현할 만큼 Gaussian을 생성하고, 엉뚱하거나 불필요한 Gaussian을 제거하도록 조절하는 과정이다.
논문에 구체적으로 명시되어있는데 다음과 같은 조절 과정을 거친다.
- 100회 iteration마다 threshold() 이하의 투명도를 갖는 Gaussian을 제거
- 3000회 iteration마다 Gaussian의 투명도를 0에 가깝게 설정
- 이어지는 학습 과정에서 투명도가 충분히 커지지 않은 가우시안이 제거되기 때문에, 효율적으로 컬링이 가능
- Scale이 너무 커진 Gaussian 제거
- Optimization 결과 threshold() 이상 이동이 필요한 Gaussian의 경우 다음과 같이 생성/분할
- Over Reconstruction - 분산이 threshold 이상일 경우 Gaussian을 두 개로 split
- Under Reconstruction - 그 외의 경우는 기존 것을 그대로 두고 옮겨야 할 위치에 Gaussian을 복제해 생성
Differentiable Tile Rasterizer

논문의 Appendix에 슈도 코드가 제공된다.
- View Space 안에 들어오는 Gaussian 만을 컬링
- World Space를 화면 좌표로 변환 (3D -> 2D)
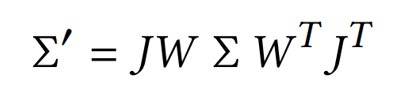
- 좌표계가 변해도 미분이 가능해야하기 때문에 Viewing Transformation Matrix(W)와 Jacobian Matrix(J)를 사용해 선형 변환을 근사한 형태로 공분산 행렬을 2x2 행렬로 변환한다.
- 병렬 처리를 위해 화면을 16x16개의 tile로 나눈 뒤, 각 타일별로 Gaussian을 컬링
- 하나의 Gaussian이 여러 타일과 겹칠 경우 인스턴스 화
- 각 인스턴스의 key는 view space depth와 tile ID를 합쳐서 생성
- key를 기반으로 Gaussian을 정렬
- 각 타일별로 카메라와 가까운 순으로 정렬 됨
- 각 타일을 구분하기 위해 타일 별로 첫 depth, 마지막 depth Gaussian을 식별해 따로 관리함
- 각 타일별로 하나의 스레드를 할당하여 GPU를 통해 병렬 렌더링
- 화면에 가장 가까운 Gaussian 부터 시작해 alpha-blending
- loss backward 과정에서 div/0 에러가 발생하지 않도록 1/255보다 작은 값은 업데이트 하지 않음
- rasterization 이전에 알파 값(투명도)을 미리 계산하여 한 픽셀의 알파 값이 일정 수치에 도달하면 해당 스레드 중지
이런 방법을 통해 loss 계산이 가능하면서도 NeRF와 달리 MLP연산 없이 병렬 처리하여 씬을 렌더링할 수 있게 되었다.
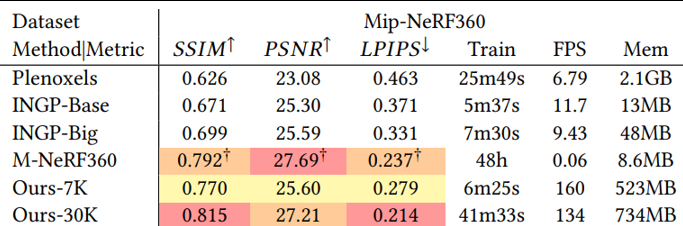
논문에 의하면 실시간 렌더링 성능이 134 ~ 160 FPS로 실시간 렌더링이 가능한 수준이다.
Loss Function
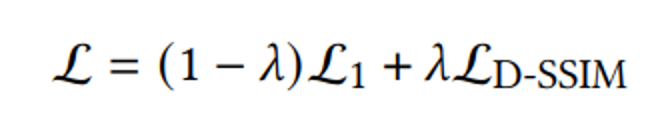
Loss Function은 L1 Loss(MAE)와 D-SSIM Loss에 가중치를 두어 사용한다.
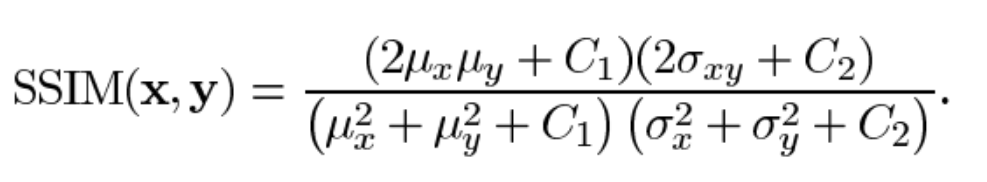
D-SSIM은 SSIM을 기반으로 한 손실 함수로, 두 이미지의 밝기(픽셀 값 크기), 대비(인접 픽셀간 차이), 구조(픽셀값 분포기반 correlation)를 이용해 두 이미지의 유사도를 계산하는 것을 기반으로 한 손실 함수이다.
논문에서는 로 사용하였다.
Limitation

- 기존 NeRF 모델에서도 발생하는 문제로, 여러 시점을 찍은 사진에서, 충분히 많이 찍히지 않는 부분에 대해 아티팩트가 발생한다는 문제가 있다.
- NeRF 기반 모델에 비해 학습에 많은 메모리가 필요하다.
- 아마 16x16 타일을 병렬 처리 하기 때문에 특히 더 많이 필요한 것으로 추정 된다
- 논문에 의하면 large scene 학습 시 이미지 한 장당 수백 MB가 필요하고, rasterizer를 위해 별도로 30-500MB가 필요하다고 한다.
- 아직 최적화 쪽으로는 고려가 많이 되지 않았기 때문에 메모리 소비를 개선할 여지가 많다고 언급하고 있다.