오늘 배운 것

선형 회귀

• 만약 아이스크림 판매 사업을 할 계획이라고 생각해보자. 사업에 있어 가장 중요한 것은 수요 예측일 것이다. 놀랍게도 아이스크림의 판매량은 고작 3가지의 요소(온도, 습도, 할인율)로 결정된다고 한다. 이는 다음과 같은 식으로 나타낼 수 있다.

판매량 = (10 * 온도) - (2 * 습도) + (20 * 할인율) + 4

• 위 식을 해석하면 온도가 1도 올라가면 아이스크림을 10개 더 팔 수 있고, 습도가 1% 올라가면 아이스크림이 2개 덜 팔리게 된다.
• 모든 조건이 0이어도 기본 4개는 판매할 수 있다.

이는 다음과 같이 나타낼 수 있다.

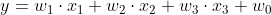
• 이렇게 타겟(y)에 영향을 주는 요인(x) 및 가중치(w), 편향(w0)으로 구성된 식을 통해 y 예측값을 구하는 것이 선형 회귀이다.

Neural Network(신경망)

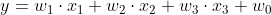
이 식은 다음과 같은 Neural Network로 나타낼 수 있다.

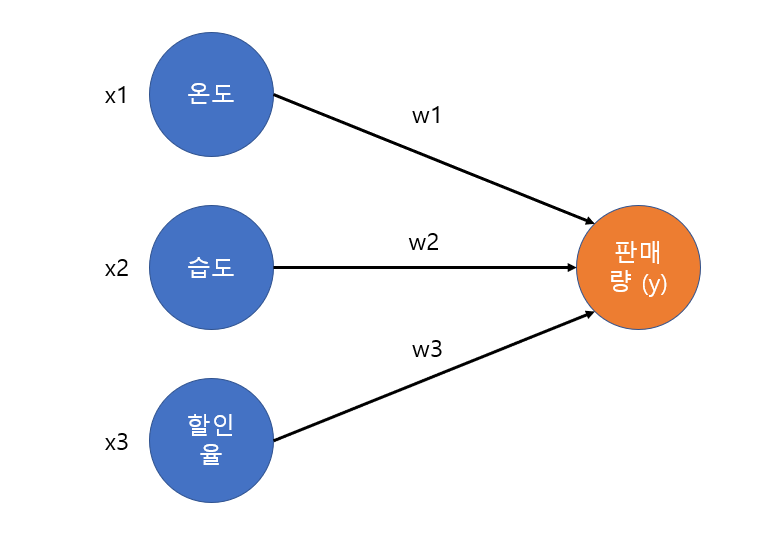
용어

• 노드 : 각 요인(x) 및 타겟(y)을 나타내는 하나의 원이다.
  • 하나의 노드는 다른 노드와 구별되는 개별적인 특징을 말한다.
• 연결(링크) : 요인과 타겟을 연결하는 선을 말한다. (Edge라고도 한다)

딥러닝 개념

• 딥러닝은 어떤 랜덤한 초기값에서 시작하여 에러를 줄이는 방향으로 가중치를 업데이트하면서 학습한다.

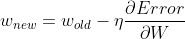
네이버 부스트 코스 수강 당시 정리한 것이 있으니 참고하자

• 딥러닝 학습방법
• 경사하강법

• 기존 가중치에서 현재 가중치에서 에러의 변화량(기울기) * 학습률을 빼줌으로써 에러가 가장 작은 정답치를 향해 업데이트 한다.
• 이때 중요한 파라미터 중 하나가 바로 학습률(η)인데, 적절한 값을 찾는 것이 중요하다.
  • 학습률이 너무 크면 가중치가 한 번에 크게 바뀌어 target에서 멀어지는 경우 발생
  • 학습률이 너무 작으면 아무리 학습을 오래 해도 local minimal에 도달하지 못하는 경우 발생
• 학습률은 보통 기본값을 따르나, 모델의 알고리즘을 지정할 때 인자로 넣어줄 수 있다.

파이썬 딥러닝 구현(선형회귀)

• 파이썬에서는 Tensorflow, PyTorch의 두 딥러닝 프레임워크를 가장 많이 사용한다. 입문자는 보통 Tensorflow, 그 중에서도 keras API를 사용하는 것을 가장 추천한다.

• keras API는 딥러닝 모델링을 쉽게 구현할 수 있는 High Level API로 딥러닝을 처음 배울 때 가장 유용하게 사용한다.

keras Sequential API

• 각 레이어(층)들을 순차적으로 결합시키는 딥러닝 모델링 AI이다.

• 용어
  • Input : 입력되는 변수 (노드)
  • Layer : 한 층을 의미, 위 그림에서 Input layer는 x1, x2, x3로 구성
  • Output Layer : 레이어 중 출력노드로 구성된 레이어
  • Densily Connected Layer : 모든 Input 노드와 Output 노드가 연결된 neural network를 말한다. Fully Connected Layer라고도 한다.

코드 구현

1. 라이브러리 불러오기

import tensorflow as tf
from tensorflow import keras

import numpy as np

• tf는 텐서플로우의 앨리어싱 관습이다.

2. 데이터 Shape 확인하기

# 모양 확인하기
x.shape, y.shape

• 딥러닝 모델링을 위해 shape을 확인하는 것은 매우 중요하다.
• 데이터의 shape대로 모델의 shape을 만들어 주어야 정상적인 학습이 진행된다.

3. 모델 발판 생성 & 레이어 쌓기

# 2. 모델 (발판) 선언

model = keras.models.Sequential()
# 모델 레이어 쌓기
model.add( keras.layers.Input(shape=(3,)) )
model.add( keras.layers.Dense(1) )

• 먼저 Sequatial API를 사용하기 위해 Sequantial 모델을 만들어 준다. 그 뒤 데이터 형태를 층층이 모델에 알려준다.
• Input Layer : Input(shape=(n, )) - n은 변수의 수를 의미 (위 그림의 경우 3)
• Output Layer : Dense(m) - m은 출력 노드의 개수를 의미 (위 그림의 경우 1)

• Sequential model에서 순서는 매우 중요하므로, 레이어를 쌓는 순서를 바꾸면 안된다.

4. 컴파일

model.compile(loss="mse", optimizer="adam")

• 모델에 적용할 학습 기준(loss)과 알고리즘(optimizer)을 선언한다.
• 딥러닝 모델은 loss를 줄이는 방향으로 가중치를 업데이트하며 학습한다.
• optimizer는 가중치를 줄이는 방향 및 얼마나 줄일지 등을 결정하여 학습을 최적화하낟.

• 이번 경우는 회귀 문제이므로 Mean Absolute Error를 줄이는 방향으로, adam을 사용해서 학습한다.

5. 학습 및 예측

# 학습
model.fit(x, y, epochs=10, verbose=2)

# 예측
y_pred = model.predict(x)

• 학습과 예측은 sklearn의 머신러닝 모델링때와 비슷하다. 단, 지정해주어야 하는 옵션이 있다.
  • epochs : 학습 횟수를 의미한다. 많을 수록 학습 데이터에 대한 성능이 높아지지만 너무 많으면 과적합 우려가 있다.
  • verbose : 학습의 진행 경과를 표시여부를 결정한다. 0, 1, 2 중에 선택할 수 있으며 보통은 진행바를 함께 볼 수 있는 기본값 1로 진행한다.

mini-batch

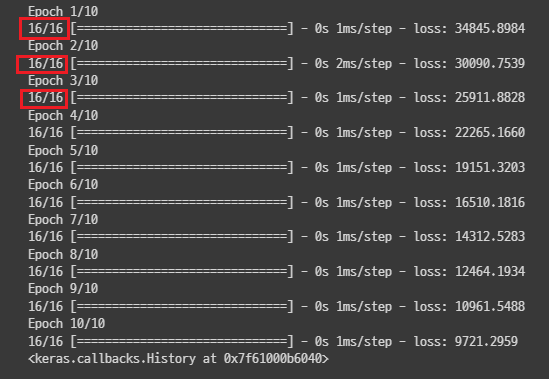
• 학습 진행 시 각 Epoch별로 표시된 네모칸과 같은 숫자를 볼수 있는데, 이는 mini-batch를 나타낸 것이다.

• 모든 데이터를 한번에 메모리에 담아 학습하면 좋겠지만, 메모리는 한정되어있기 때문에 어려움이 있다. (batch)

• 대신 전체 데이터를 메모리에 넣을 수 있는 수준으로 쪼개어 데이터를 나누어 업데이트 하는 것을 mini-batch라고 한다. 모든 mini-batch를 업데이트 해야 1번의 Epoch 사이클을 돈 것으로 간주한다.

• 위 사진의 16/16은 16개의 mini-batch로 나누었고, 모든 mini-batch에 대해 학습을 완료했다는 것을 의미한다.

• mini-batch 사이즈는 model.fit(mini_batch= ) 옵션으로 설정할 수 있으며 기본값은 32이다.

Logistic 회귀 (binary)

• 머신러닝에서 배웠듯 Logistic 회귀는 선형 회귀식을 바탕으로 분류 문제를 풀 때 이용한다.
• 하지만 분류 문제를 풀기 위해서는 범위 (0, 1)의 확률값을 이용해야 하는데, 선형회귀식을 사용하면 범위가 무한대로 가는 문제점이 있다.
• 머신러닝에서 이를 sigmoid 함수를 적용하여 해결했듯이, 딥러닝에서도 동일하게 적용할 수 있다.
• 즉, 비선형함수인 sigmoid 함수를 한단계 더 거치는 것으로 Logistic 회귀를 이용한 딥러닝 학습을 할 수 있게 된다.

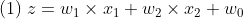
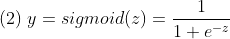
코드 구현

• 다른 것은 선형 회귀와 모두 동일하지만, Dense layer를 쌓을 때 적용할 활성함수를 activation 인자로 함께 선언하면 된다.

• 또한 회귀 문제와 분류 문제는 평가 지표가 다른 만큼 crossentropy라는 다른 loss를 사용한다.
  • 0과 1의 두가지로 분류하는 문제일 경우 loss=binary_crossentropy이다.
  • 평가지표를 직관적으로 확인하기 위해 보조지표를 사용하기도 하는데, metrics='accuracy' 인자를 전달하면 정확도가 보조지표로써 함께 표시된다.

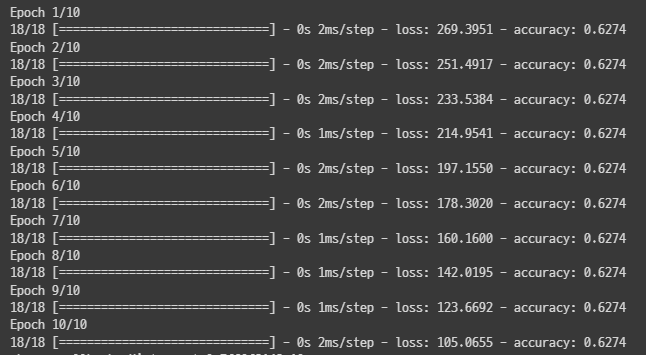
• 출력 결과로 0 ~ 1의 확률값을 얻을 수 있다. 더 가까운 쪽을 해당 클래스로 선택한다.

멀티 클래스 분류 문제

• 위의 경우는 클래스가 0과 1 두가지인 경우였지만, 클래스가 세 개 이상일 경우에는 다소 복잡해진다.

One v.s. rest

• 멀티 클래스 분류 문제를 풀기 위한 전략으로, 모든 클래스에 대해 각각 학습 및 sigmoid 함수를 하여 0~1의 확률 값을 구한 뒤 이들을 비교해 확률이 가장 높은 것을 선택하는 방법이다.

• 그러나 예를 들어 클래스가 A일 확률이 0.4, B일 확률이 0.6, C일 확률이 0.2라면 이들의 합은 1.2로 확률의 범위를 벗어나버린다. 때문에 지금 구한 값은 확률이 아니며, 여전히 이대로 예측에 사용할 수 없는 형태이다.

softmax 함수

• softmax 함수는 입력 받은 값을 0~1로 정규화 하여 출력하는 함수로, 출력값의 총합은 항상 1이되는 특성을 갖는 함수이다.

• 즉 sigmoid를 거친 값들을 다시 softmax로 변환하면 범위가 (0, 1)이고 합계가 1인 확률값으로 변환된다. 이들 중 가장 높은 확률을 갖는 클래스를 예측값으로 최종 선택 한다.

One-Hot Encoding

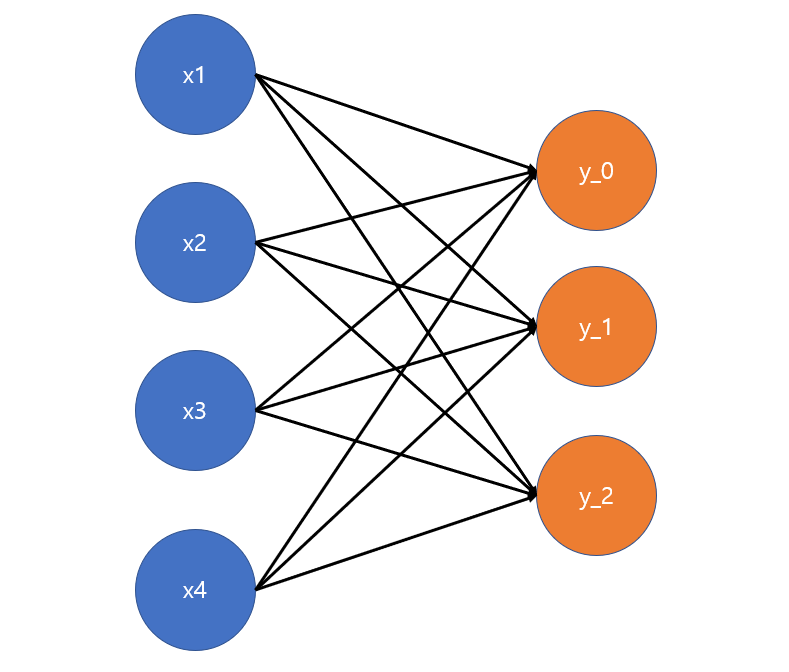
• 그런데 보통 target는 데이터의 변수 중 하나를 선택한 것으로 1차원 데이터이다.
• One v.s. rest를 사용하려면 각각의 노드에 학습 및 sigmoid를 적용해야 하므로 이를 클래스별로 쪼개야한다.
• 이 때 사용하는 것이 바로 One-Hot Encoding이다. keras가 제공하는 to_categorical 함수를 통해 target의 shape를 클래스 수 만큼 늘려줄 수 있다.

# One-Hot Encoding
from tensorflow.keras.utils import to_categorical

# 클래스 3개로 shape 늘리기
y = to_categorical(y, 3)

주의 사항 : to_categorical은 실행될 때마다 y의 형태를 늘리므로 반복 실행하지 않도록 주의해야 한다.

코드 구현

• 클래스가 2개일 때인 Logisitic 회귀와 비슷하지만, to_categorical로 쪼개는 과정을 거쳐야 하고, activation 함수로 sigmoid 대신 softmax를 사용해야 한다.

• 또한 loss function으로 categorical_crossentropy를 사용한다.

정리

	선형 회귀	로지스틱 회귀	멀티 클래스
activation	선언 X (또는 linear)	sigmoid	softmax
loss	mse	binary_crossentropy	categorical_crossentropy

추가로 공부한 내용

softmax 함수

• softmax 함수는 어떻게 input 벡터를 합계가 1인 벡터로 바꾸어서 출력하는 걸까?
• 공식은 아래와 같다.

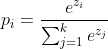
가령 A:0.4, B:0.6, C:0.2를 softmax에 input으로 준다고 가정하자

import numpy as np

def softmax(vec):
    numerator = np.exp(vec - np.max(vec, axis=-1, keepdims=True))
    # vec의 max값을 빼주는 이유는 지수함수이므로 값이 너무 커지면 overflow가 발생할 수 있기 때문이다. 
    # 분모는 분자의 합이기 때문에 분자가 달라져도 결과에 영향을 주지 않는다.
    denominator = np.sum(numerator, axis=-1, keepdims=True)
    val = numerator / denominator
    return val


vec = np.array([0.4 , 0.6 , 0.2])
val = softmax(vec)

print(val)

[0.32893292 0.40175958 0.2693075 ]

• 합이 1임을 확인할 수 있으며 이 경우 확률이 가장 높은 B가 예측값으로 선택된다.

crossentropy

1. 엔트로피

• 엔트로피는 정보이론에서 불확실성을 수치화 한 것이다. 불확실성은 말 그대로 어떤 정보일지 예측이 안된다는 것이다.
  가령 공이 10개 들어있는 상자에서 하나를 꺼낸다 했을 때, A가 5개, B가 5개일 경우 꺼낼 공이 무슨 색일지 맞추기 어렵다.
  반대로 A가 9개, B가 1개라면 비교적 자신있게 꺼낼 공이 A라고 할 수 있을 것이다.
  전자의 경우가 큰 불확실성, 즉 엔트로피가 높은 경우이다.

• 엔트로피는 다음과 같은 수식으로 나타낼 수 있다.

1. A 3개, B 3개가 든 상자에서 공을 꺼낼 경우
   
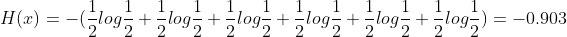
   ※ -0.903이 아니라 0.903이 맞다. (png써야해서 수식 수정도 못하는 velog...)

2. A 5개, B 1개가 든 상자에서 공을 꺼낼 경우
   

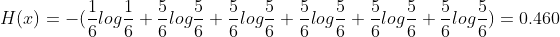
• 즉 1의 엔트로피가 더 높고 이는 불확실성이 더 높다는 것이다.

• 이는 log함수 때문인데 확률이 0에 근접할 수록 로그값은 음의 무한대로 발산하며, 앞에 음의 부호가 붙으므로, 매우 큰 엔트로피를 갖게 된다.

2. crossentropy

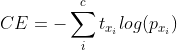
• crossentropy는 x의 실제확률(t)과 예측확률(p)를 통해 구할 수 있다.

• 만약 실제확률이 [0, 0, 1]이고 예측을 [0. 0. 1.]로 정확히 했다면 (예측 확률이 결코 0이 될순 없다) CE = 0이 된다.

• 하지만 만약 A:0.3, B:0.6, C:0.1로 예측했다면
  

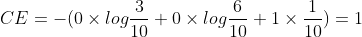
  또 수식이 조금 잘못됐는데 마지막이 1 * log(1/10) = -1이고, 앞에 음의 부호가 붙으므로 CE = 1이 된다.

이렇게 loss값이 증가하게 된다.

즉 분류를 정확히 해야 CE가 감소하기 때문에 모델이 loss를 낮추는 쪽으로 학습하게 된다.

소감

• 생소한 개념이 많이 등장한 데 반해, 실제 강의는 코드 작성 위주로 배우다 보니 이해는 잘 안되지만 슉 하고 넘어간 부분이 너무 많았다.

• 오늘 정리한 softmax와 crossentropy는 이 중 일부일 뿐이고, 진도는 점점 빨라지기만 할 것이라 솔직히 다소 걱정이 된다.

• 배울 수 있는 것만 확실히 배우고 넘어가도록 하자.