이전 게시글

4. Fundamental Matrix

Essential Matrix를 구할 때에는 두 카메라가 canonical camera라고 가정하였다.

그러나 현실의 카메라에 적용하기 위해서는 canonical이 아닌 카메라에 대응하는 Matrix가 필요하다. 이것이 바로 Fundamental Matrix이다.

두 카메라의 Intrinsic Matrix를 고려했을 때의 projection matrix($M, M'$)는 다음과 같다.

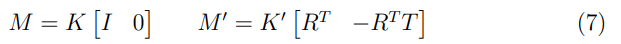
먼저 canocical camera에서 다음과 같은 방정식을 유도했다.

여기서 $p, p'$는 intrinsic matrix가 항등행렬일 때의 투영점이므로, 역행렬을 이용하여 canocical camera의 투영점($p_c, p'_c$)와 non-canonical camera($p, p'$)의 투영점과의 관계를 정의할 수 있다.
$p_c = K^{-1}p, \\ p'_c = K'^{-1}p'$

즉 Eq. 5 식을 non-canonical camera에 적용하면 다음과 같다.

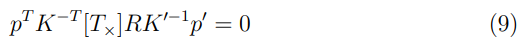
위 식을 통해 Fundamental Matrix를 $F = K'^{-T}[T_{\times}]RK'^{-1}$로 정의할 수 있다.

Essential Matrix때와 동일하게 $l' = F^Tp, l = Fp'$ 식을 이용해 epipolar line을 계산할 수 있다.

Essential Matrix의 자유도는 5로, 3차원 회전정보로부터 3, 위치 정보로부터 2의 자유도가 더해진다.
Fundamental Matrix의 자유도는 7로, Essential Matrix의 자유도에 더해 Intrinsic 정보로 인해 2의 자유도가 더해진다고 한다.

어째서 Intrinsic 정보로 인해 2의 자유도가 더해지는 것인지는 좀 더 공부하 필요하다

이렇게 얻어낸 Fundametal Matrix의 의의는 $F$만 알 수 있다면, 월드 좌표계의서 P의 위치나, 카메라에 대한 정보 없이도 두 이미지 평면의 투영점 $p, p'$ 사이의 관계를 알 수 있다는 것이다.

4.1 Eight Point Algorithm

기본적으로 Fundamental matrix는 카메라의 정보로 계산되지만, 카메라 정보가 없어도 Eight Point 알고리즘을 통해 추정할 수 있다.

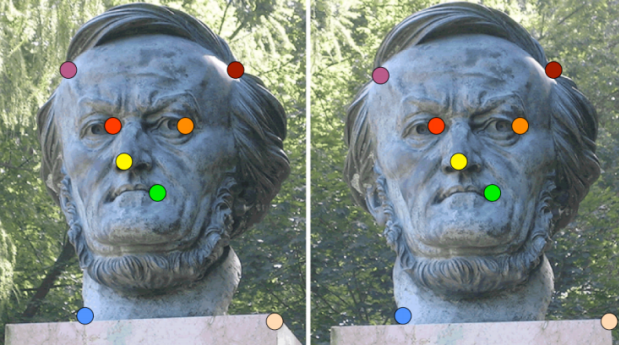
위와같이 두 이미지 사이에 동일한 지점을 나타내는 최소 8개의 point 집합을 사용한다. (8개보다 많으면 일반적으로 더 좋다)

Epipolar geometry에서 유도된 Eq. 6 방정식($p_i^TFp'_i = 0$)을 이용하여 다음과 같은 식으로 재표현할 수 있다.

여기서 $W$는 $N \geq 8$개의 포인트 집합이며, $\mathbf{f}$는 Fundametal Matrix의 각 성분을 벡터로 펼친 것이다.

여기에 특이값 분해(SVD)를 통해 최소제곱법으로 접근하여 F에 대한 예측값 $\hat{F}$을 얻을 수 있다.

$F$는 skew-symmetric 행렬인 $T_{\times}$로 부터 계산되었으므로 rank 2라는 것을 알 수 있다.
즉 rank-2 approximation으로 SVD를 풀 수 있다.

수학적으로 문제를 정의하면 다음과 같다.

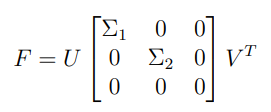
아직 SVD에 대해 잘 알지 못하다보니 이해가 안가는 부분이 많다.. SVD와 rank-2 approximation에 대해서는 별도로 공부가 필요할 것 같다.

4.2 The Normalized Eight-Point Algorithm

앞서 Eight Point 알고리즘에 대해 설명했지만, 실제로는 그다지 정확하지 않다.
그 이유는 최근의 고해상도 이미지에서는 $p_i = (1832, 1023, 1)$ 와 같은 값이 사용되기 때문에 하나의 특이값이 0(또는 0에 가까운) 값이 어야하는 SVD에 적합한 조건이 만들어지지 않을 가능성이 높다.

이를 방지하기 위해서 $W$ 행렬을 구성하기 전에, 각 포인트들을 정규화하는 과정을 거쳐야한다.

정규화 과정을 위해 이미지 좌표계를 다음의 두 조건을 만족하도록 전처리한다.
1. 조정된 좌표계의 (0, 0)은 이미지의 중앙이다.
2. 조정된 좌표와 원점 사이의 mean squeare distance는 2픽셀이다.

이를 수학적으로 나타내면 다음과 같다.

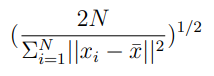
이렇게 좌표를 정규화하는 변환 행렬을 $T, T'$라고 하고, 정규화된 좌표계에서 구한 Fundametal Matrix를 $F_q$라고 할 때 $F = T'^TF_qT$로 원래의 Fundametal Matrix를 구할 수 있다.

5. Image Rectification

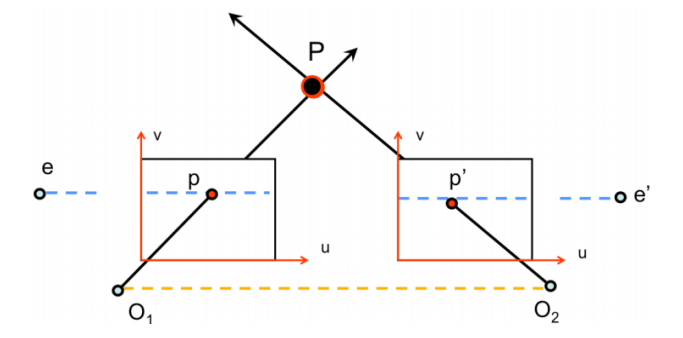
Epipolar geometry에서 두 카메라 평면이 평행할 때 여러가지 흥미로운 케이스를 볼 수 있다.

두 카메라는 평행하므로 회전이 없고(회전 행렬이 항등행렬), 두 카메라가 x축 방향으로 정렬되어있다. $(T=(T_x, 0, 0)$
즉, Essential Matrix를 다음과 같이 구할 수 있다.

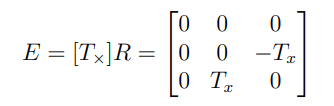
이렇게 구한 Essential Matrix를 통해 epipolar line의 방향 역시 구할 수 있다.

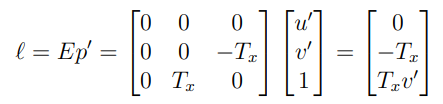
이를 통해 두 카메라가 평행할 때 epipolar line이 수평선임을 알 수 있다.

앞서 사용한 $p^TEp' = 0$을 이용하면 $v = v'$라는 결과를 얻을 수 있다.

이렇게 두 이미지 평면을 평행하게 만들어주는 과정을 Rectification이라고 하며, rectification 과정을 통해 두 이미지의 대응점 간의 관계를 파악할 수 있다.

평행하지 않은 두 이미지를 Rectify하는 것에는 Fundamental Matrix가 사용된다.

앞서 Eight Point 알고리즘으로 추정한 F값을 이용해 두 이미지의 epipolar line($l_i, l'_i$)을 구할 수 있다.

이렇게 epipolar line을 알면 epipoles($e, e'$) 역시 예측할 수 있는데, epipoles는 항상 epipolar line 위에 있기 때문에, 모든 epipolar line이 교차하는 지점이 바로 epipoles가 된다.

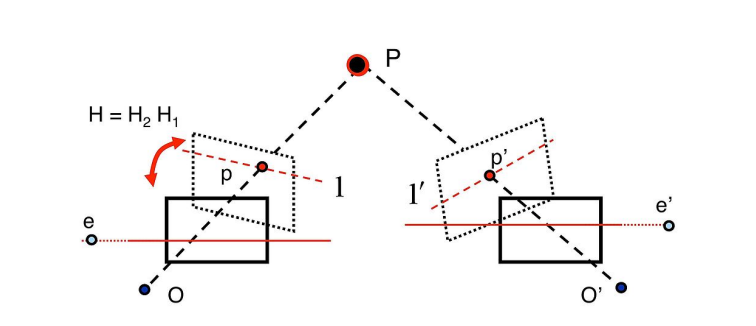
두 이미지가 평행할 때는 epipoles가 infinity에 위치한다(f, 0, 0)는 것을 고려하면,
epipoles가 infinity가 되는 시점이 바로 두 이미지가 평행한 시점이며
epipoles를 infinity로 보내는 두 homography $H_1, H_2$를 찾는 것이 rectification 문제이다.

우선 두번째 평면의 $e'$를 (f, 0, 0)으로 변환하는 $H_2$를 다음과 같이 정의할 수 있다.

먼저 두번째 이미지 평면의 중점이 (0, 0, 1)이 되도록 translation 및 rotation을 해주어야 한다.

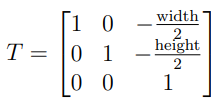
translation을 적용한 후에는 epipole이 수평축에 위의 (f, 0, 1)에 위치하도록 rotation을 적용한다.

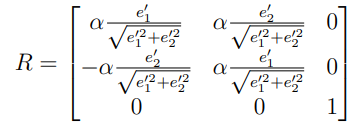
epipole을 infinity인 (f, 0, 0)으로 보내는 변환을 적용한다.

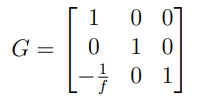
마지막으로 변환된 좌표계를 다시 원래대로 되돌리는 과정을 통해 두번째 이미지 평면을 rectify하는 homography $H_2$를 정의하는 과정을 다음의 식으로 나타낼 수 있다.

이제 올바르게 정의된 $H_2$를 바탕으로, 여기에 매칭되는 $H_1$을 찾는 문제가 남았다.

$H_2$에 의해 변환된 투영점 $H_2p'$ 역시 수평선인? epipolar line위에 있으므로, $H_1, H_2$에 의해 변환된 두 투영점 간의 거리가 최소가 되도록 하는 $H_1$을 찾는 문제로 볼 수 있다.

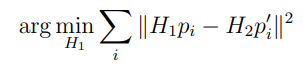
그리고 이어서 증명 및 유도 과정이 나오는데...
여기서부터는 아직 도저히 이해할 수가 없었다.

결론적으로는 위의 최소 거리가 되는 $H_1$을 찾는다면 두 이미지를 rectify하여 두 이미지 간의 관계를 알 수 있다는 것이 주요 내용이었다.

참고 자료

https://faceyourfear.tistory.com/72