1. Introduction
이전 강의 노트에서는 하나의 Scene에 대한 하나 이상의 이미지들로부터 Scene에 대한 특징 정보를 유도할 수 있었다.
하지만 3D Scene에서 2D Image로 맵핑하는 과정에서 특징 정보가 손실될수밖에 없다.

대표적으로 위 사진에서 우리는 직관적으로 피사의 사탑이 사람보다 훨씬 뒤에 있다(depth가 깊다)라는 것을 알 수 있지만, 사전 지식이 없다고 할 때, 여기서 피사의 사탑과 인물의 depth 차이와 같은 geometry 정보를 복원할 수 없다.
이러한 geometry 정보를 얻기 위해 Epipolar geometry를 알아보자
2. Epipolar Geometry
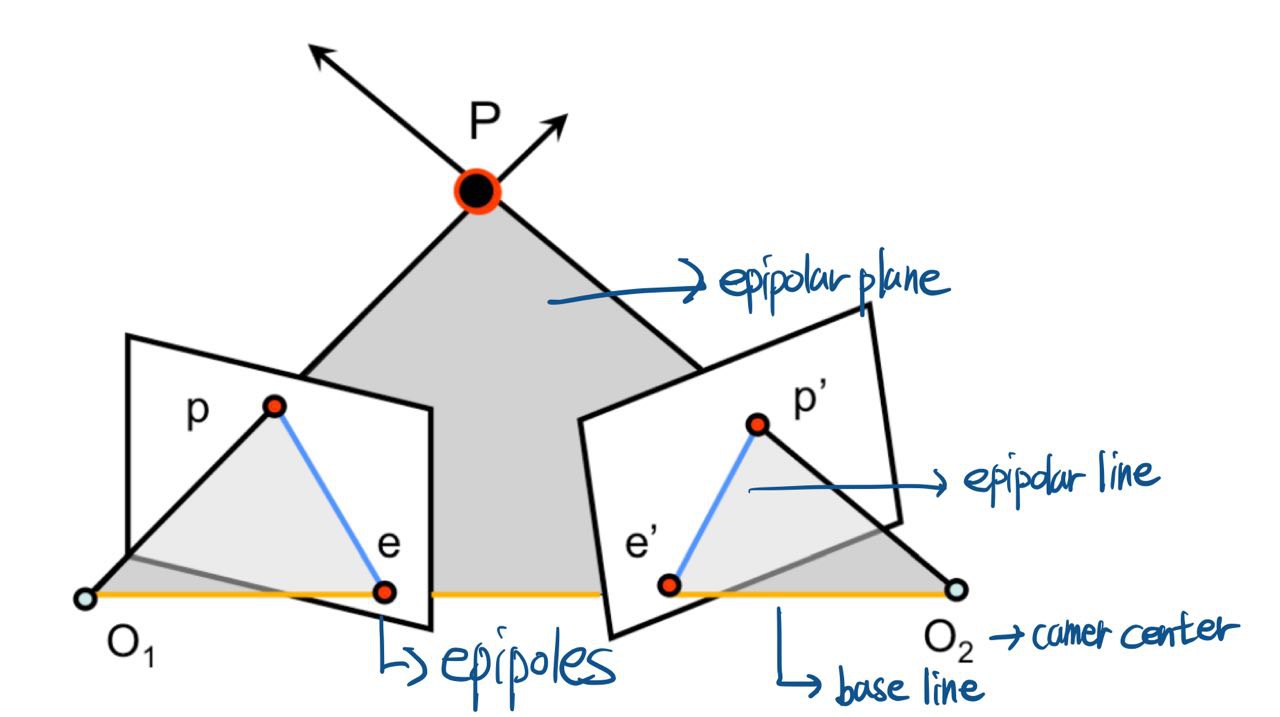
Epipolar Geometry는 하나의 대상를 서로 다른 두 위치의 카메라에서 투영한 이미지 평면에 대한 geometry이다.
- epipolar plane : 두 카메라의 중심()과 대상(P)으로 구성된 삼각형 평면
- baseline : 두 카메라의 중심을 연결한 선
- epipoles(): baseline과 두 image plane의 교차점
- : 대상(P)을 각각 이미지 평면에 투영했을 때의 위치
- epipolar line(): epipole과 투영점을 이은 선
우리가 알고자 하는 것은 3D Scene에서의 대상 P의 정보이다. 그리고 이를 epipolar plane을 통해 구할 수 있다는 것이 이번 강의 내용의 핵심이 되는 것 같다.
원래라면 두 카메라의 위치와 각 카메라의 intrinsic matrix, extrinsic matrix를 알아야 epipolar plane을 정의할 수 있을 거이다.
하지만 epipolar geometry에서는 카메라 정보를 모른다고 해도, 두 카메라의 위치와 투영된 이미지 상의 한 점 p만으로 이를 정의할 수 있다고 한다.
이것이 어떻게 가능한 것인지에 대해 배워보자
3. The Essential Matrix
한 카메라의 투영점 p를 기준으로 하면, 나머지 하나의 투영점 p'는 한 카메라()를 카메라()로 이동하는 변환 벡터()와 기준 image plane을 나머지 image plane으로 변환하는 회전()로 표현할 수 있다.
이 때 두 카메라의 정보를 담은 projection matrix()는 다음과 같이 정의할 수 있다.
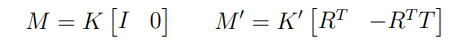
문제를 단순하게 하기 위해서 두 카메라가 canonical camera라고 가정하자.
canonical camera란 카메라의 intrinsic matrix가 표준화된, 즉 항등 행렬인 카메라를 말한다.
그러면 가 되어 식을 다음과 같이 단순화 할 수 있다.
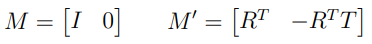
이 경우 가 된다.
또한 역시 카메라 변환 벡터이므로 두 점 는 모두 epipolar line위에 존재한다.
사실 T가 어떻게 epipolar line 위에 있다는 것인지 잘 이해가 되지 않는다... 선형 변환을 제대로 공부해야하나...
즉 두 벡터를 벡터곱하여 epipolar line의 normal vector를 얻을 수 있다.
epipolar line 위의 점 p와 normal vector를 내적하면 영벡터가 되기 때문에 최종적으로 다음과 같이 표현할 수 있다.

선형 대수에서 벡터간의 벡터곱은 다음과 같이 미분가능한 행렬-벡터간 곱셈으로 나타낼 수 있다.
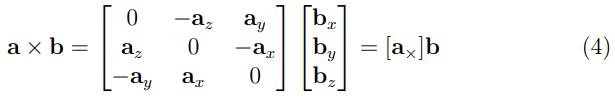
이를 이용하여 앞서 구한 3번식을 다음과 같은 행렬곱으로 표현할 수 있다.

여기서 구한 3x3 행렬을 Essential Matrix라고 한다.
이 Essential Matrix()는 점 p와 점 p' 사이의 기하학적 관계를 정의 한다.
E와 p를 곱하면 Essential Matrix가 담고 있는 기하학적 정보를 바탕으로 잠재적으로 image plane 2에서 p에 대응될 수 있는 모든 잠재적인 점을 epipolar line이라는 선으로 나타내게 되는 것이다.
예를 들어 카메라 2의 epipolar line()은 이다.
마찬가지로 카메라 1의 epipolar line은 이다.
의 또다른 propetry는 epipoles와의 내적값이 항상 0이라는 것이다. epipoles는 항상 epipolar line( - 는 epipolar line 위의 임의의 점) 위에 있기 때문이다.
즉 이 된다.
