강의 노트 원본은 여기서 받으실 수 있습니다.

핀홀 카메라

핀홀 카메라는 가장 기본적인 형태의 카메라로, 빛을 차단하는 배리어에 바늘 구멍을 뚫어 어두운 상자 안에 상이 투영되도록 한다.

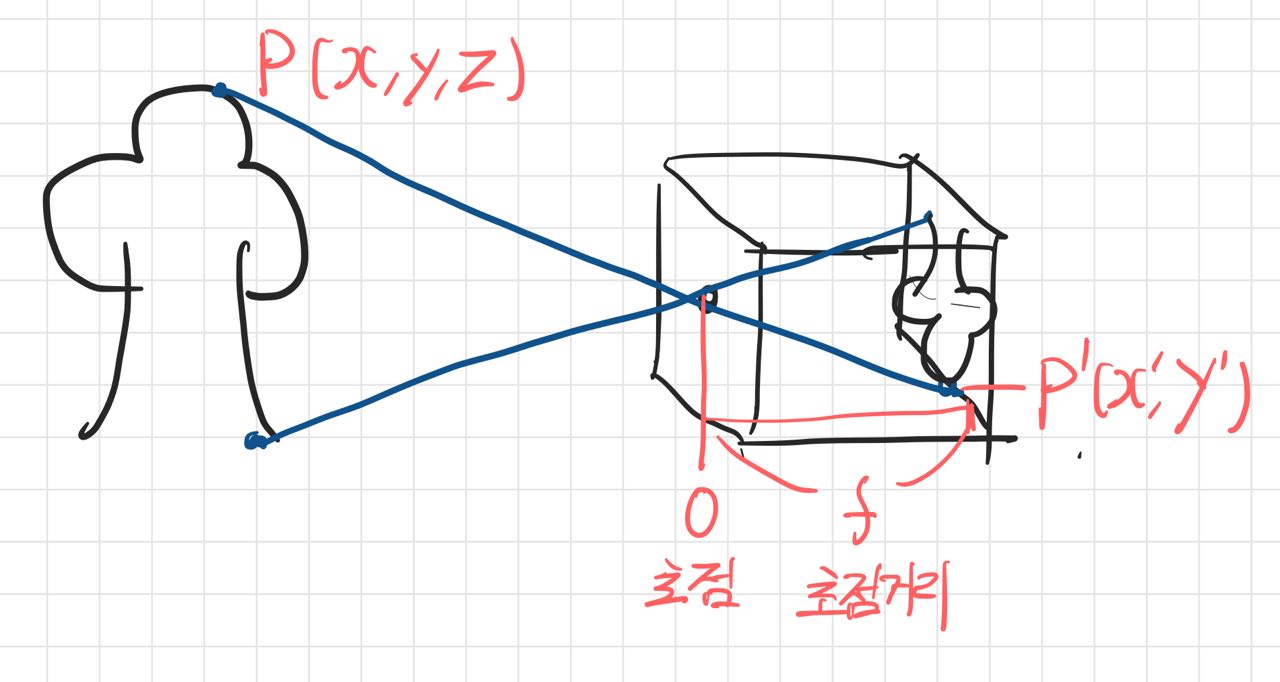
핀홀 카메라를 z축 방향으로 정렬한 그림으로 나타내면 다음과 같은데, 3차원의 현실 상을 2차원의 image plane으로 투영한다.

이 때 핀홀을 초점으로, 초점과 이미지 플레인 사이의 거리를 초점 거리(focal length)로 하여 P → P' 변환 방정식을 얻을 수 있다.

렌즈 카메라

변환 방정식

핀홀 카메라의 단점은, 선명한 상을 얻기 위해 좁은 구멍이 필요한데 구멍이 좁아질수록 얻을 수 있는 상이 어두워진다는 것이다. 반대로 구멍을 넓게하면 빛이 넓게 퍼져 선명함을 잃는다.

이러한 단점을 극복한 렌즈 카메라는 다음과 같은 구조를 갖는다.

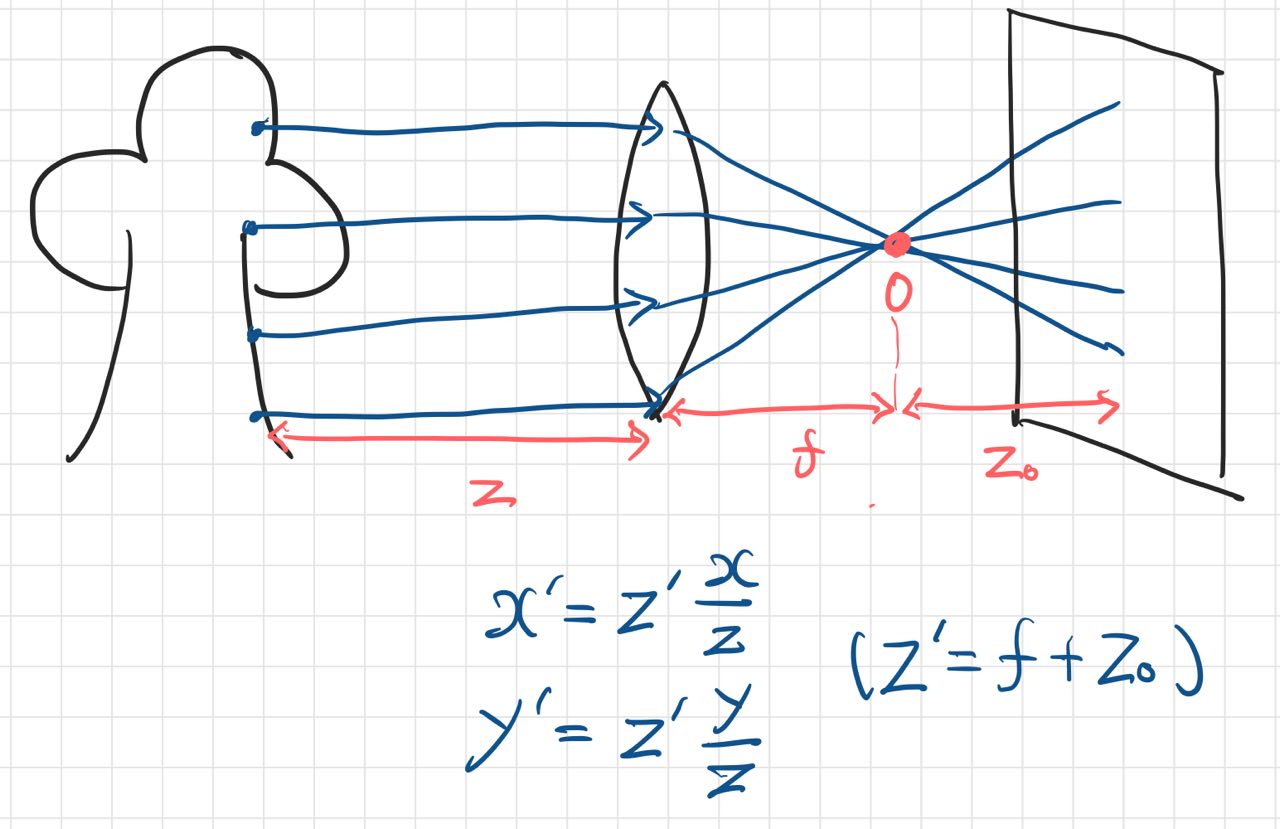
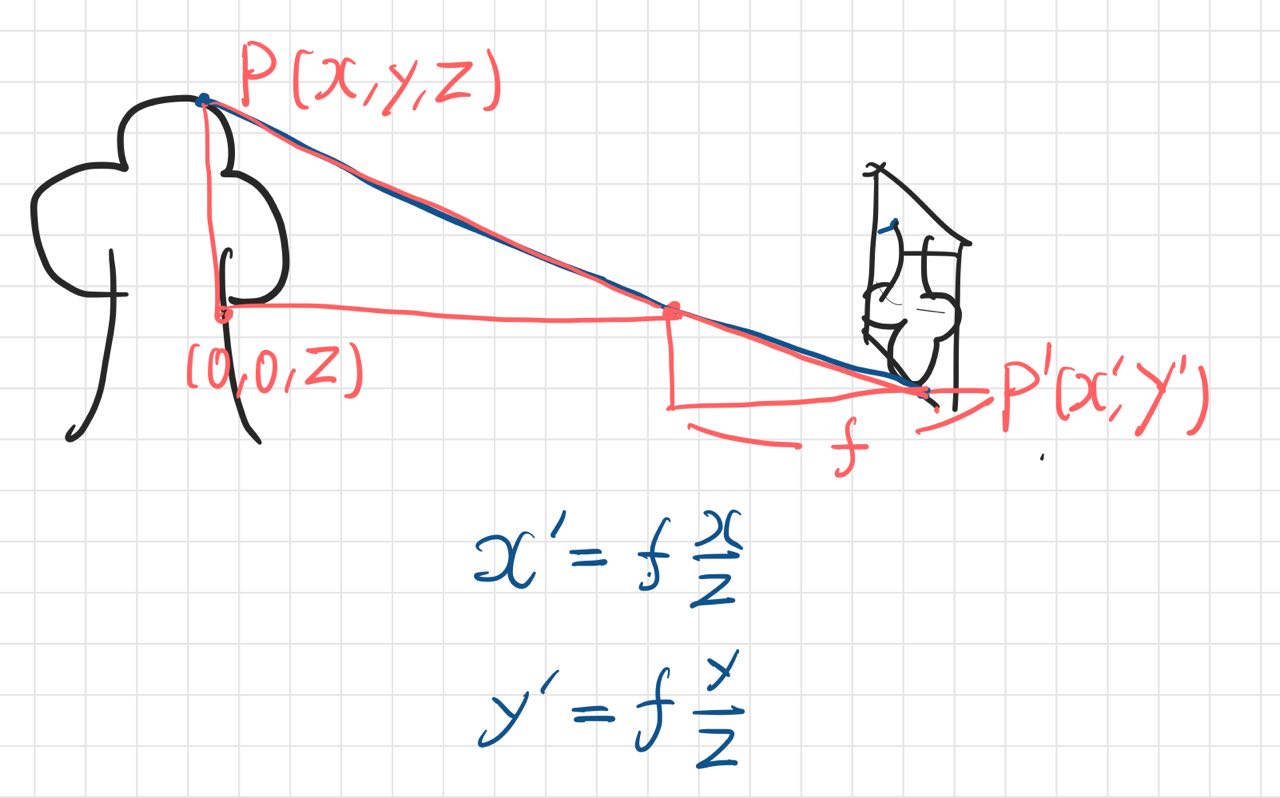
렌즈에 의해 굴절된 빛이 한 점으로 모이는 지점이 발생하며,
렌즈와 초점 사이의 거리(f), 초점과 이미지 평면 사이의 거리($z_0$) 두 개의 거리를 얻게 된다.
두 거리를 더한 $z'$으로 초점 거리를 얻을 수 있기 때문에 아까와 마찬가지 방법으로 정리할 수 있다.

Camera Metrix Model

이렇게 얻은 2D 투영 이미지는 아직 컴퓨터가 계산할 수 없다.
이를 컴퓨터가 계산할 수 있도록 만들기 위해서는 두가지 과정을 거쳐야 한다.

좌표계 변환

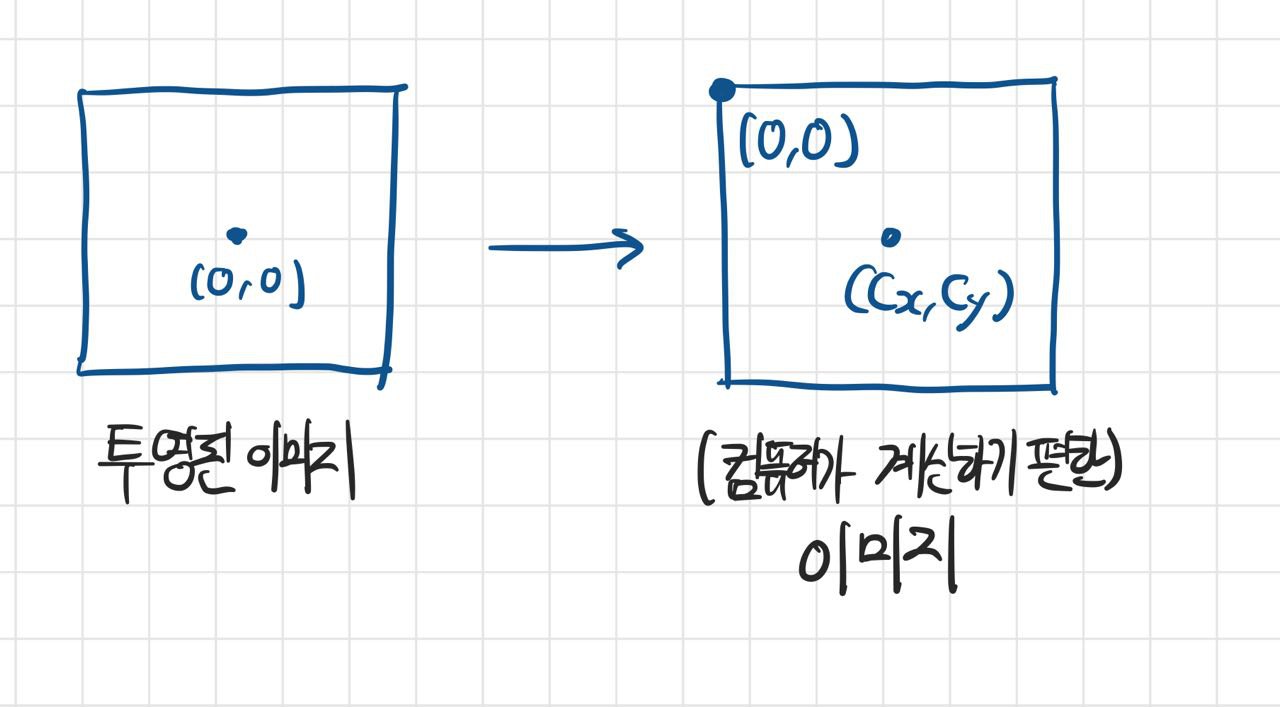
중심점을 원점으로 계산한 이미지 평면의 좌표와 달리 컴퓨터의 2차원 행렬에서는 일반적으로 왼쪽 위를 원점으로 한다.

이를 위해 이미지의 크기에 비례하여 좌표를 옮기는 shift 과정이 필요하다.

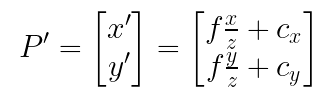
픽셀 변환

다음으로는 연속적인 물리값(cm)을 이산적인 픽셀로 변환해주어야 한다.
여기서 변환비는 $\frac{pixel}{cm}$가 되며 각 축별 변환비를 k, l로 나타낸다.
만약 이미지의 종횡비가 같다면 k = l이 된다.

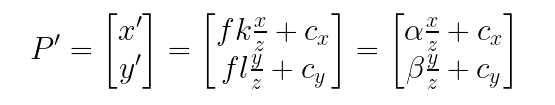
그런데 이 형태는 비선형 변환(input 값중 하나인 z로 다른 input값을 나누는)이다.
3D Scene에서의 변환(이동, 회전, 크기)로 인해 새로운 x', y'을 계산하거나 앞으로 CV를 위해 미분을 해야할 때 여러모로 계산이 어려울 수 있다.

이를 해결하기 위해 Homogeneous Coordinate system을 이용해 투영 과정을 하나의 행렬곱으로 나타낼 수 있다.

Homogeneous Coordinate system

Homogeneous Coordinates는 n차원의 사영 공간을 n+1개의 좌표로 나타내는 방법으로
예를들어 (x, y, z)의 좌표를 (wx, wy, wz, w)로 나타낼 수 있다.
w=1일 때 Homogeneous Coordinates(x, y, z, 1)가 원래의 좌표를 나타낸다.

Homogeneous Coordinates를 사용하는 궁극적인 이유는 앞서말한 이동, 회전, 크기와 같은 변환을 모두 행렬곱으로 나타낼 수 있기 때문이다.

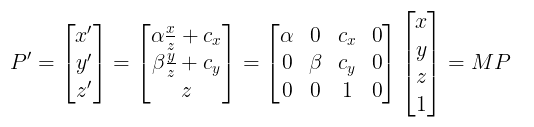
Camera Parameters

사람마다 똑같은 사물을 보더라도, 보이는 색상, 모양 등이 다르듯이 각각의 카메라 상을 투영할 때 고유의 성질(파라미터)를 갖는다.

Intrinsic Parameter

Intrinsic Parameter는 카메라의 고유 성질로 총 5가지가 있다.

• $\alpha, \beta$ : 픽셀 크기, 초점 거리 등의 카메라 성질
• $c_x, c_y$ : 카메라가 투영하는 상의 크기
• $\theta$ : 여기에 더해 카메라 제조시에 발생하는 미세한 오류로 발생하는 왜곡(distortion)과 렌즈에 의해 발생하는 뒤틀림(skewness)을 나타내는 파라미터

Extrinsic Parameter

카메라의 고유 성질과는 상관 없는 파라미터로, 실제로 가만히 있는 물체(월드 좌표계)를 다른 위치, 다른 각도에서 보면 다르듯이(view 좌표계) 카메라의 위치(T), 회전(R)에 따라 투영되는 이미지가 변하는 것을 나타내는 파라미터이다.

위치 3차원, 회전 3차원으로 총 6가지의 파라미터가 있다.

$P' = K [R \; T]P_w = MP_w$

요약하자면 카메라를 통해 이미지를 투영하기 위해 3 X 4의 변환 행렬(M)을 이용하며, Intrinsic Parameter 5 + Extrinsic Parameter 6으로 총 11개의 파라미터를 결합하여 표현할 수 있다.

코멘트

글을 쓰면서도 횡설수설하는 것을 느껴질 정도로 아직 이해가 충분한 것 같지 않다.

특히 Camera Calibration 쪽은 정리할 엄두가 안날 정도로 아직 이해가 부족하다...

우선 다음 개략적인 이해를 하고 다음 내용을 먼저 살펴본 뒤 다시 돌아와서 이해해보도록 하자