Background

NFSD는 SDS Loss의 한계를 극복하기 위해 새롭게 제안된 loss입니다.

SDS Loss에 대해서는 이전 게시글에서도 다루었지만, 다시 읽어보니 너무 글을 못 쓴 것 같아서 다시 간략하게 설명하고자 합니다.

딥러닝 및 생성형 모델을 배우기 시작한지 얼마 안되었기 때문에 틀린 부분이 있을 수도 있습니다. 이런 부분을 발견하신다면 지적해주시면 정말 감사하겠습니다.

SDS Loss

SDS Loss는 매우 뛰어난 성능을 보이는 2D diffusion model의 강력함을 다른 분야의 학습에 적용하기 위한 loss입니다. Diffusion model이 현실(또는 목표한 분야)의 분포를 아주 잘 학습하였으니, diffusion model의 가중치는 고정시켜 놓고, 어떤 미분 가능한 이미지 렌더러가 diffusion model이 갖고 있는 분포를 근사하도록 설계되었습니다.

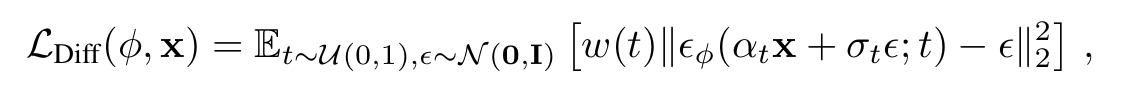
이 수식은 DDPM 논문에서 제시된 Diffusion Model의 loss입니다.
$\phi$는 모델의 U-Net 모델 파라미터입니다. U-Net은 timestep $t$만큼 노이즈가 더해진 이미지를 입력받아 이미지에 더해진 노이즈를 예측합니다 ($\epsilon_\phi$). $\epsilon$은 실제 더해진 노이즈입니다.

SDS는 이 DDPM의 loss를 변형한 형태라고 볼 수 있습니다.
먼저 input 이미지 $\mathbf{x}$가 실제 이미지가 아닌 NeRF에 의해 렌더링된 이미지 $\mathbf{x} = g(\theta)$입니다. 여기서 $\theta$는 NeRF 모델의 파라미터입니다.

우리가 학습하고자 하는 것은 $\theta$이므로 loss를 $\theta$로 편미분하여 구한 그라디언트로 업데이트하면, 현실의 분포를 잘 모방하는 NeRF를 학습할 것이라 기대할 수 있습니다.

이제 실제로 편미분을 해보겠습니다.

$\frac{\delta L}{\delta \theta} = \frac{\delta L}{\delta \hat{\epsilon}} \frac{\delta \hat{\epsilon}}{\delta \mathbf{x}} \frac{\delta \mathbf{x}}{\delta \theta}$

$\frac{\delta L}{\delta \hat{\epsilon}} = 2w(t)(\hat{\epsilon}-\epsilon)$

$\frac{\delta \hat{\epsilon}}{\delta \mathbf{x}} = \alpha_t \frac{\delta \epsilon_\phi(\alpha_t \mathbf{x} + \sigma_t \epsilon ; t)}{\delta (\alpha_t \mathbf{x} + \sigma_t \epsilon)}$

여기서 $\hat{\epsilon}$은 U-Net의 output을 간소화하여 표현한 것입니다.

이렇게 해서 나온 것이 DreamFusion 논문의 식 2번입니다.
실제 이미지 대신 latent $\mathbf{z}_t$가 사용되었고, condition $y$(여기서는 text 임베딩)가 추가되었다는 점이 다릅니다.
또 $\alpha_t$는 특정 $t$에서의 상수로 간주하여 $w(t)$로 흡수시켰다고 합니다.

DreamFusion에 의하면 U-Net Jacobian으로 인한 문제가 있다고 합니다.
그라디언트 계산을 위해 U-Net 전체에 대해 역전파를 진행해야 해서 계산이 너무 무거워지고, small noise level에 적합하지 않다고 합니다.

때문에 U-Net Jacobian term을 아예 제거한 것을 score로 사용한 것이 바로 SDS Loss입니다.

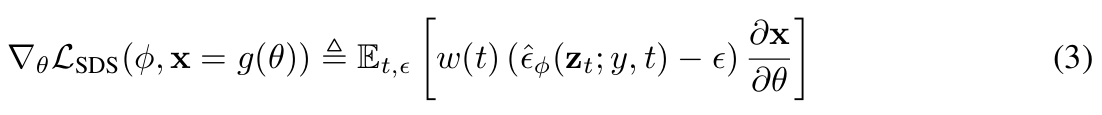
SDS Loss의 한계

text-to-image task를 수행하는 최신 diffusion model은 대부분 CFG(Classifier-Free Guidance)를 적용합니다. 이 부분은 아직 저도 자세히 공부하지 못했기 때문에 이런걸 쓴다 정도로만 짚고 넘어가겠습니다.

CFG를 적용할 때 CFG계수($s \in \mathbb{R}$)를 정하는데, $s$가 클수록 diversity는 감소하지만 렌더링 품질이 좋아진다고 합니다. 하지만 너무 높을 경우 over-saturated한 이미지를 얻게 됩니다.

일반적으로 diffusion model에서는 대략 8정도의 값을 사용한다고 합니다. 하지만 SDS loss를 적용했을 때는 $s = 100$ 정도로 높은 값을 적용해야한 학습이 잘 이루어진다고 합니다.
이로인해 학습된 NeRF로 렌더링된 이미지마저 over-staurated하고, 사실적이지 못한 경우가 많았습니다.
이외에도, SDS loss로 학습하여 렌더링된 이미지가 over-smoothed한 문제도 있었습니다.

NFSD는 SDS loss를 세 개의 구성요소로 쪼개어, 왜 높은 $s$에서만 학습이 이루어지는지를 해석하고, 필요없는 구성요소를 제거함으로써 일반적인 $s$값에서도 학습이 잘 이루어질 수 있도록 하는 새로운 loss를 제안했습니다.

이제 이 새로운 NFSD loss에 대해서 설명하고자 합니다.

NOISE-FREE SCORE DISTILLATIONNOISE-FREE SCORE DISTILLATION 논문 리뷰

Score Decomposition

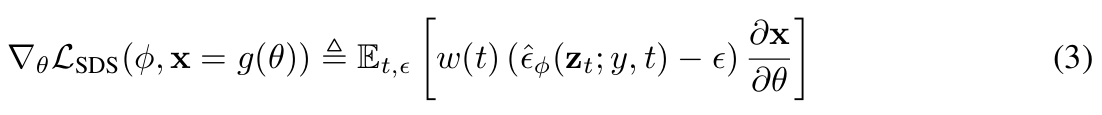
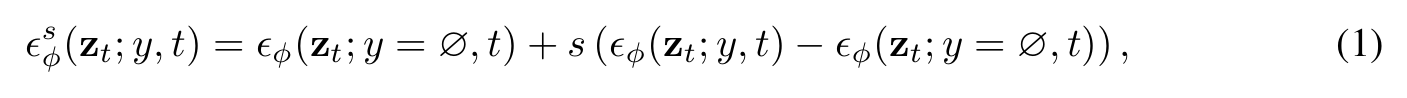
SDS Loss의 $\hat{\epsilon}_\phi$에 대해 CFG를 적용한 것이 $\epsilon^s_\phi$입니다.
$\epsilon_\phi(\mathbf{z}_t; y, t)$는 condition $y$를 적용한 노이즈 예측 결과, $\epsilon_\phi(\mathbf{z}_t; y=\varnothing, t)$는 condition이 없는(null condition) 예측 결과입니다.

NFSD는 이 U-Net의 노이즈 예측 결과를 아래와 같이 3개의 컴포넌트로 쪼개어 생각했습니다.

$\delta_C = \epsilon_\phi(\mathbf{z}_t; y, t) - \epsilon_\phi(\mathbf{z}_t; \varnothing, t)$
$\delta_D + \delta_N = \epsilon_\phi(\mathbf{z}_t; \varnothing, t)$

$\delta_C$

먼저 $\delta_C$에 대해 살펴보면, 좌항은 input condition $y$에 해당하는 노이즈 이미지의 확률 밀도의 local maximum을 향하는 term이라고 해석할 수 있습니다. 반면 우항은 컨디션이 없는 이미지의 확률 분포가 더 조밀한 곳을 향하는 term입니다.

좌항에서 우항을 뺐다는 것은, 생성한 이미지가 condition $y$와 일치하도록 유도하는 방향만 남는 것이라고 해석할 수 있습니다.

논문에서는 이를 condition direction이라고 명명했습니다.

$\delta_D, \delta_N$

나머지 $\delta_D, \delta_N$에 대해 살펴보자면, 앞서 말한 unconditional term을 두 컴포넌트로 쪼갠 것입니다.

이렇게 쪼갤 수 있는 이유는 바로 noisy한 latent $\mathbf{z}_t$가 NeRF에 의해 렌더링된 이미지($\mathbf{x} = g(\theta)$)로부터 얻어진 것이기 때문입니다.
U-Net은 현실의 이미지 분포에 노이즈를 더한 것을 학습했는데, (학습이 덜 된) NeRF의 분포는 이와 다르기 때문에 out-of-distribution(OOD) 문제가 발생합니다.

논문에서는 이렇게 이미지의 분포와, U-Net이 학습한 분포가 맞지 않는 것을 domain이 다르다고 하여 out-domain이라 하고, 동일한 분포를 사용할 경우에는 in-domain이라고 하였습니다.

즉, NeRF 파라미터 $\theta$에 의해 생성된 이미지에 대한 unconditional term에는 노이즈가 제거된 이미지를 향하게 하는 $\delta_N$ 외에도, out-domain에서 in-domain 분포로 향하게 하는 $\delta_D$가 존재한다고 가정하였습니다.

논문에서는 $\delta_N$을 denoising direction, $\delta_D$를 domain correction이라고 명명했습니다.

Score Decomposition을 통해 SDS loss를 다시 나타내면 아래의 수식이 완성됩니다.

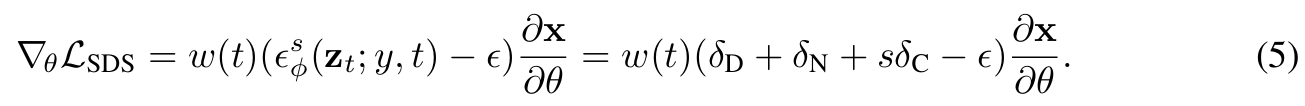
Noise-Free Score Distillation

denoising direction의 문제점

앞서 설명드렸듯이 SDS loss의 목표는 주어진 condition에서 diffusion model의 확률 분포를 학습하는 것입니다.
즉, 우리는 NeRF가 렌더링한 이미지가 input condition에 맞도록, diffusion model의 확률 분포에서 샘플링한 것과 맞도록 $\theta$를 조정하는 것에만 관심이 있습니다.

앞서 정의한 바에 의하면 $\delta_D, \delta_C$는 이를 잘 수행하는 term입니다.
반면 $\delta_N - \epsilon$은 그렇지 못합니다. 오히려 랜덤한 non-zero 노이즈이기 때문에 $\theta$를 랜덤한 방향으로 이끈다고 합니다. 이것이 iteration 과정에서 쌓이면 averaging effect가 발생하여 over-smoothed한 이미지가 생성되도록 유도합니다. 이는 이미지의 fine-detail을 학습하는 낮은 timestep에서 특히 심하게 영향을 준다고 합니다.

이 해석은 SDS에서 높은 CFG 계수를 사용해야 학습이 잘 이루어지는 이유에 대해서도 설명할 수 있습니다.

식 5번에서 $s$가 매우 클 경우 $\delta_C$가 loss의 대부분을 차지하게 되어 나머지 term을 어느정도 무시할 수 있게되기 때문에 학습이 잘 이루어지는 것입니다.
하지만 앞서 말했듯 높은 $s$는 사실적이지 못하고 over-saturated한 이미지를 렌더링하기 때문에 근본적인 해결책은 되지 못합니다.

NFSD Loss

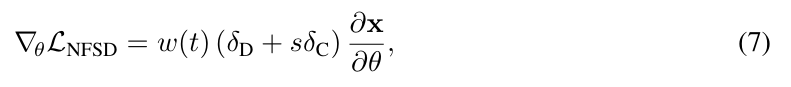
기존의 SDS loss에서 학습을 방해하는 $\delta_N - \epsilon$을 제거한 것이 NFSD loss입니다.

문제는 $\delta_N$을 unconditional term( $\epsilon_\phi(\mathbf{z}_t; \varnothing, t)$ )으로부터 분리하는 것입니다.
$\delta_N, \delta_D$는 개념적으로 분리한 것이지, 명시적으로 분리할 수 있는 수식이 없기 때문입니다.
논문에서는 $\delta_D$에 대해 한가지 멋있는 가정을 세워서 이를 해결했습니다.

$\delta_D$ 분리하기

앞서 condition direction $\delta_C$는 이미지가 주어진 condition $y$에 정렬되도록 유도하는 방향을 나타낸다고 설명했습니다.

그렇다면 이런 condition direction도 만들 수 있습니다.

$\delta_{C=p_{neg}} = \epsilon_\phi(\mathbf{z}_t; y=p_{neg}, t) - \epsilon_\phi(\mathbf{z}_t; \varnothing, t)$
$p_{neg} =$ 나쁜(학습하고자 하는 것과 반대되는 이미지를 생성하는) 프롬프트의 분포
→ 나쁜 프롬프트의 예 : unrealistic, blurry, low quality, out of focus, ugly, dull, gloomy etc.

앞서 말한 논문의 멋진 가정은 다음과 같습니다.

• $\delta_D \approx -\delta_{C=p_{neg}}$

즉, $\delta_D$는 high-fidelity, realistic한 고품질의 이미지를 생성하는 diffusion model의 domain을 향하는 방향인데, 여기에 반대되는 이미지를 생성하는 프롬프트로 유도하는 방향은 $-\delta_D$라고 가정한 것입니다.

이를 통해 $\delta_D$를 분리하는 아래의 식을 유도할 수 있습니다.
$\epsilon_\phi(\mathbf{z}_t; \varnothing, t) - \epsilon_\phi(\mathbf{z}_t; y=p_{neg}, t) = \delta_D + \delta_N - (\delta_{C=p_{neg}} + \delta_D + \delta_N) \approx \delta_D$

최종 loss

여기에 한가지를 더 고려하면, timestep이 낮을 때는 noise가 적게 추가된 상태이기 때문에 $\epsilon_\phi(\mathbf{z}_t; \varnothing, t) = \delta_D + \delta_N$에서 $\delta_N$이 무시할 수 있을 정도로 작다고 합니다.

논문에서는 이 timestep $t$의 threshold를 200으로 설정하였습니다.

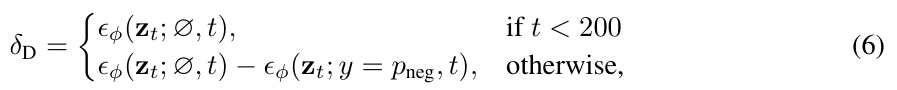
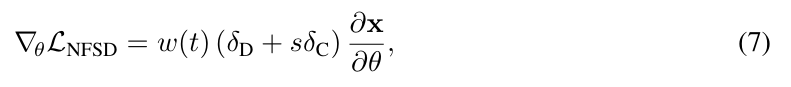
결론

이렇게 noisy한 term이 제거된 NFSD loss는 over-smoothed 문제를 해결하였고, 낮은 CFG 계수(7.5 정도)에서도 학습이 잘 이루어지도록 만들었습니다.

자세한 렌더링 결과는 NFSD 프로젝트 페이지에서 확인하실 수 있습니다.

여기서는 다루지 않았지만, ProlificDreamer와 같이 기존의 SDS Loss를 개선한 연구에 대해서 왜 개선이 되었는지를 $\delta_N, \delta_D, \delta_C$ 관점에서 설명한 부분도 너무 좋은 내용인 것 같습니다.

참고문헌

NFSD 논문
Noise-Free Score Distillation - Ostin X - 티스토리