[논문 리뷰] LucidDreamer: Towards High-Fidelity Text-to-3D Generation via Interval Score Matching
논문

일부는 저의 해석이 들어가 있어서 잘못된 부분이 있을 수 있습니다. 혹시 잘못된 부분이 있다면 지적 부탁드립니다.
text-to-3D
LucidDreamer는 text-to-3D 생성 모델을 학습하기 위한 손실 함수에 대해 중점적으로 다루고 있습니다.
text-to-3D의 역사에 대해 짧게 짚고 넘어가보면, 인터넷에 있는 풍부한 텍스트-이미지 쌍을 학습 데이터로 쓸 수 있던 text-to-image 모델들(i.e. CLIP, Stable Diffusion)과는 달리 3D 분야는 이런 대규모 데이터셋을 구할 수 없다는 것이 문제였습니다.
이러한 문제를 해결하고자 Dreamfusion 논문에서 SDS(Score Distillation Sampling)라는 새로운 접근법을 제시합니다.
SDS는 pretrained diffusion 모델을 현실의 분포를 잘 나타내는 ground truth로 간주하고, 3D 생성 모델(i.e. NeRF, 3DGS)이 생성하는 결과의 분포를 diffusion 모델이 갖고 있는 분포와 일치시키는 것을 목표로 합니다.
diffusion 모델의 지식을 3D 생성 모델로 증류(distill)한다고 하여 SDS라는 표현을 사용한 것 같습니다.

Dreamfusion 예시
SDS는 추후 설명할 SDS loss를 스코어로 사용하여 3D 생성 모델을 업데이트 하는데, 생성 결과가 over-smoothing 되어 디테일한 표현이 부족하거나, 색상이 과장되게 표현되는 등의 문자가 발생했습니다.
LucidDreamer는 SDS loss의 어떤 점 때문에 이런 문제가 발생하는지 분석하고, 이를 해결하는 새로운 loss를 제시합니다.
Revisiting the SDS
SDS loss
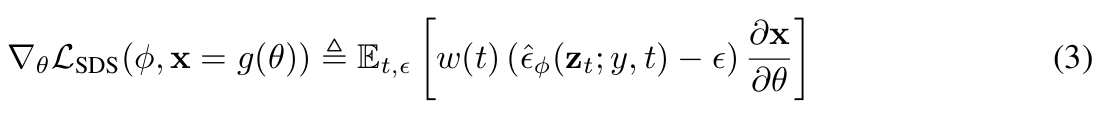
SDS loss 수식은 다음과 같습니다. 이를 구하는 과정을 간단히 정리해보자면
- NeRF 로 특정 view의 이미지를 렌더링
- 이미지 크기와 같은 랜덤 가우시안 노이즈 생성
- timestep 에 따라 렌더링된 이미지에 노이즈를 더함
- pretrained diffusion model의 U-Net에 노이즈 이미지를 넣어 더해진 노이즈를 예측
- 실제 더해진 노이즈와 예측된 노이즈의 차이를 score로 사용하여 NeRF 모델의 파라미터 를 업데이트
SDS Loss에 대한 자세한 설명은 구글에 검색하시거나, NFSD 논문 리뷰의 Background 문단에 짤막하게나마 설명된 부분을 참고해주시길 바랍니다.
SDS loss의 문제점
SDS loss 수식 재해석
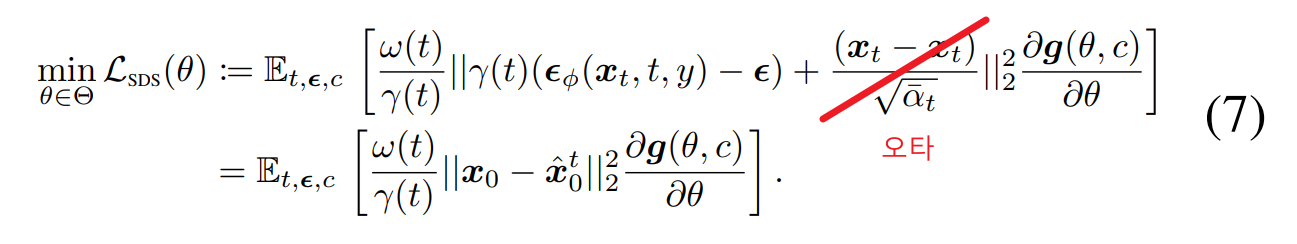
- noisy image :
- pseudo-GT :
위 세가지 식을 이용해서 기존의 SDS loss의 변수를 치환하면 Eq. 7의 아래와 같은 식을 얻을 수 있습니다.
이 해석대로라면 SDS loss는 모델이 생성한 이미지()가 pseudo-GT()를 따라가도록 학습하는 손실 함수라고 볼 수 있습니다.
여기서 pseudo-GT는 에서 U-Net이 예측한 노이즈를 뺀 값으로, 보다 pretrained diffusion model이 학습한 현실의 분포를 잘 반영하고 있는 이미지입니다. 지도학습에서 train data와 동일한 역할을 하기 때문에 pseudo-GT라는 표현을 사용한 것 같습니다.
이렇게 재해석된 관점에서 봤을 때, 논문에서는 ground truth 역할을 하는 pseudo-GT의 품질이 낮기 때문에, pseudo-GT로 학습한 모델의 성능 역시 낮다고 합니다.
pseudo-GT의 품질이 낮아지는 원인에는 크게 두 가지가 있는데, 이제 두 가지 문제점이 어떤 것인지 설명하겠습니다.
노이즈의 랜덤성
첫번째는 pseudo-GT를 생성하기 위해 이미지에 더해지는 노이즈가 완전히 랜덤이라는 점입니다.
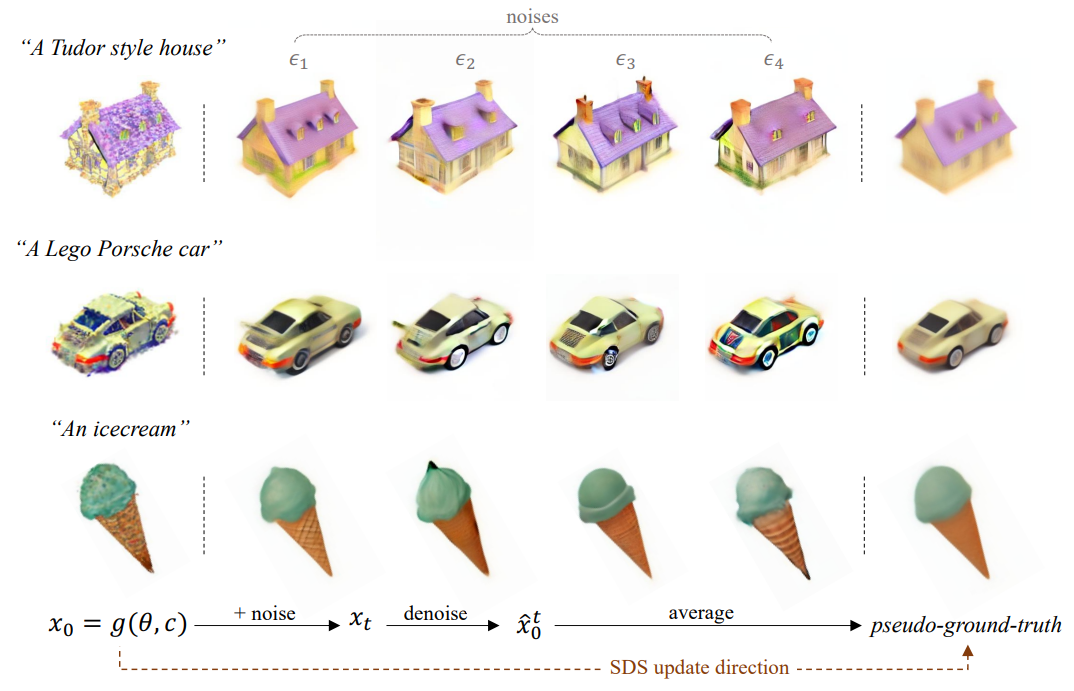
위 figure에서 첫번째 열에 있는 그림은 3D 생성 모델의 결과(), 2~5열에 있는 그림은 생성 결과에 서로 다른 랜덤 노이즈()를 더한 결과(입니다.
figure에서 보시다시피, 노이즈가 랜덤이기 때문에 의 결과가 매번 달라지는 것을 확인할 수 있습니다. 이러한 차이들이 매 스탭마다 누적되면 결국 마지막 열의 그림처럼 평균화되어 blurry한 결과로 학습이 이루어집니다.
논문에서는 이러한 노이즈의 랜덤성이 SDS로 학습한 모델이 over-smoothing된 결과를 렌더링하는 현상의 원인이라고 합니다.
단일 스탭 denoise로 인한 높은 error
- pseudo-GT :
위 식에서 보면 알 수 있듯이 timestep에 상관없이 pseudo-GT를 구하는 것에는 단 한번의 예측만을 수행하고 있습니다.
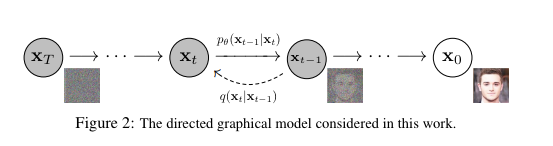
문제는 위 그림과 같이 순차적인 단계로 노이즈를 예측하도록 학습된 DDPM 모델 특성상, 이렇게 단일 스탭으로 노이즈를 예측하면 높은 reconstruction error가 발생합니다.
이로인해 단일 스탭으로 예측된 노이즈로 계산된 pseudo-GT는 디테일이 떨어지고 블러리하다고 논문은 주장합니다.
요약
요약하자면 SDS는 pretrained diffusion model을 이용해 pseudo-GT를 만들고, 3D 생성 모델이 이를 따라가도록 학습합니다.
그러나 SDS loss에서 pseudo-GT는 노이즈의 랜덤성, 높은 reconstruction error로 인해 그 품질이 원래의 diffusion model에 미치지 못합니다.
LucidDreamer는 (1) DDIM Inversion이라는 랜덤성이 낮은 노이즈 생성 방식, (2) ISM(Interval Score Matching)이라는 새로운 접근법을 통해 효율적으로 reconsturction error를 낮추어 이러한 SDS의 단점을 개선하고자 합니다.
Methodology
DDIM Inversion
수식적인 내용이 필요 없으시다면 바로 다음 섹션(Pseudo-code)로 넘어가주시기 바랍니다.
DDIM Inversion으로 noisy 이미지 를 만드는 방법에 대해 설명하겠습니다.
- 기존 방식 :
기존 방식에서는 에서 곧바로 랜덤한 노이즈를 더합니다.
- DDIM Inversion
- 일 때
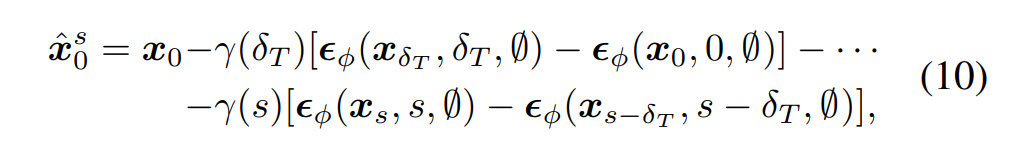
DDIM inversion은 다음과 같이 순차적인 방식으로 를 만듭니다. 이 과정을 풀어서 설명하자면 다음과 같습니다.
1. 다음 타임스탭의 noisy 이미지 계산
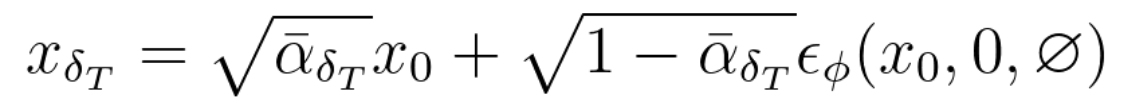
기존에는 단순히 랜덤한 가우시안 노이즈를 생성해 더했지만
DDIM inversion에서는 pretrained U-Net이 예측한 노이즈를 더합니다.
2. denoise
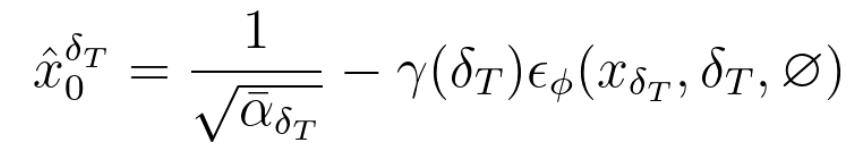
를 사용하여 형태가 달라졌지만, 앞서 설명한 pseudo-GT를 구하는 식과 동일한 식입니다.
이 과정은 로 노이즈 수준을 초기로 되돌리는 역할을 합니다.
3D 생성 모델의 분포로 생성된 와 달리 는 조금 더 diffusion 모델의 분포가 반영되어있다고 해석할 수 있습니다.
3. 다시 다음 타임스탭의 noisy 이미지 계산 (1~2를 까지 반복)
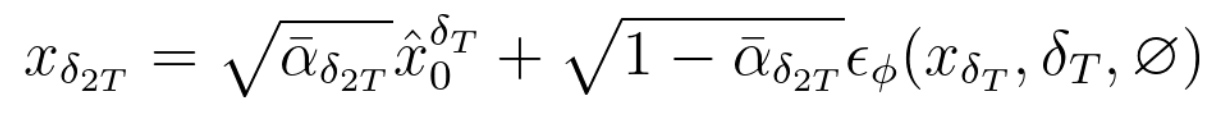
1~2를 순차적으로 반복하면서 에 도달할 때 까지 계산을 반복합니다.
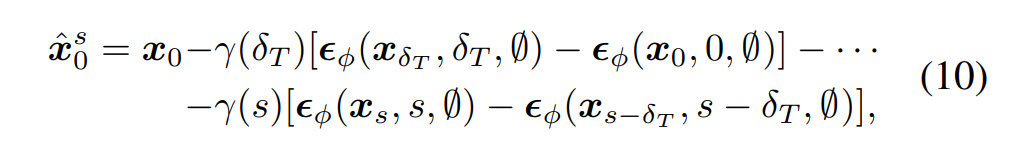
Eq. 10은 위 과정을 정리하여 수식으로 나타낸 것입니다.
이렇게 를 생성하면 더이상 랜덤한 노이즈를 사용하지 않는다는 장점이 있습니다. 즉 동일한 입력 에 대해 항상 동일한 를 생성한다는 것이 보장됩니다. 때문에 DDIM inversion은 평균화로 인한 over-smothing 문제를 상당히 완화할 수 있다고 합니다.
또한, 이렇게 모델의 예측값을 바탕으로 를 생성하는 것이 pretrained diffusion model의 분포를 3D 생성 모델로 증류한다는 SDS의 사상에 더 적합하다고 생각합니다.
Interval Score Matching(ISM)
이제 를 denoise하여 pseudo-GT를 계산하는 과정을 거쳐야합니다.
앞서 SDS는 단일 스탭으로 노이즈를 예측하기 때문에 높은 reconstruction error가 발생하여 denoise된 pseudo-GT의 디테일이 떨어지고 블러리하다는 문제가 있었습니다.
사실 이 문제는 단일 스탭이 아닌 멀티 스탭을 통해 순차적으로 노이즈를 예측한다면 근본적으로 해결될 수 있습니다.
멀티 스탭 디노이즈
DDIM을 이용해 순차적으로 pseudo-GT()을 구하는 식은 다음과 같습니다.
-
DDIM Inversion에서 를 구하는 식
-
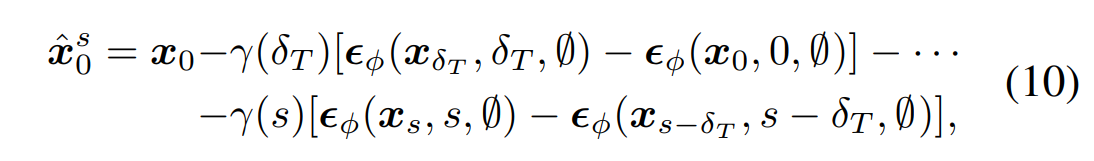
-
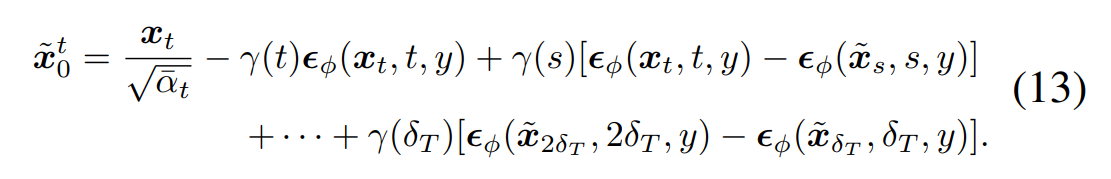
제가 직접 전개하지는 못했지만, 논문에 의하면 SDS에서 pseudo-GT를 구하는 식을 DDIM에 맞게 적용한 것이 DDIM Inversion에서 를 구하는 식이며, 이를 부터 까지 순차적으로 적용한 것을 정리한 식이 Eq. 13입니다.
이렇게 멀티 스탭으로 pseudo-GT를 계산한다면 reconstruction error를 최소화 할 수 있습니다.
그러나 이렇게 멀티 스탭으로 denoise를 할 경우 연산 비용이 증가한다는 것이 문제가 됩니다.
ISM 유도
앞서 설명한 연산 증가 문제를 완화하기 위해서, ISM은 멀티 스탭에서 최대한 필요 없는 term을 제거하여 최소한의 연산으로 사이의 차이를 최소화 하는 것을 목표로 합니다.
다시 앞서 DDIM Inversion에 사용된 수식과 Eq. 13을 들고오겠습니다.
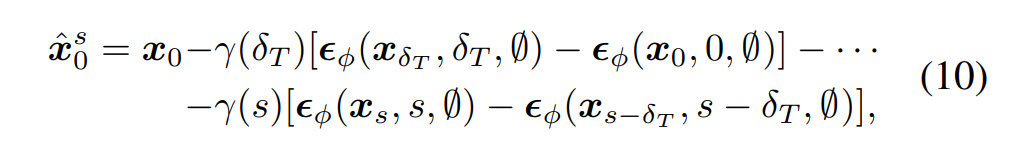
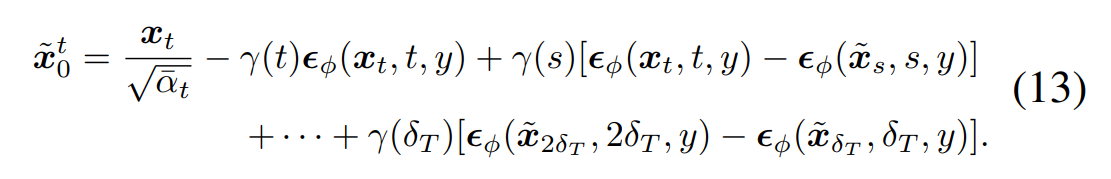
먼저 Eq. 10에서 를 구할 수 있는데, 이므로
이기 때문에 Eq. 10의 을 Eq 13에 대입하여 최종적으로 아래의 식을 얻게 됩니다.
여기서 공통된 형식을 보이는 끼리 묶어서 라고 정의했을 때
이렇게 최종적으로 로 나타낼 수 있게 됩니다.
이를 바탕으로 ISM Loss의 계산식을 구할 수 있습니다.
ISM Loss
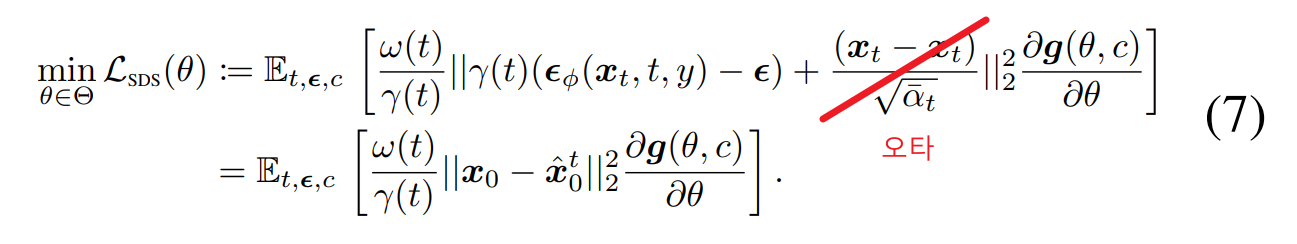
앞서 Eq. 6으로 정의한 SDS loss에서 를 로 교체하면 DDIM inversion, ISM을 적용한 loss term이 됩니다.
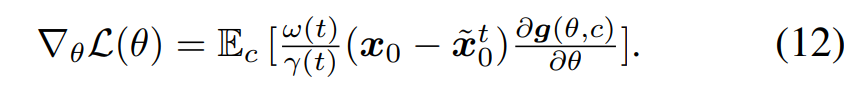
Eq.12에 를 대입합니다.

이렇게 정리된 수식만으로는 여전히 멀티 스탭으로 pseudo-GT를 구하는 수식입니다.
논문에서는 는 3D에 대한 것보다는 에 밀접하게 관련이 있는 term이기 때문에 연산의 효율성을 위해 제거해도 무방하다고 합니다.
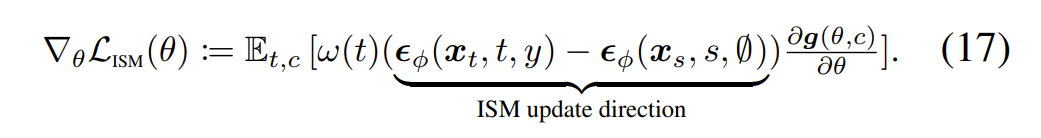
를 제거하면 비로소 논문이 제안하는 ISM Loss term이 됩니다.
이렇게 하면 모든 timestep에 대해 노이즈를 예측할 필요 없이 딱 두 timestep에 대해서만 노이즈를 계산하는 two-step-prediction이 되어 연산 비용을 훨씬 절약할 수 있습니다.
에 대한 자세한 실험 및 증명은 논문의 supplements에 첨부되어 있습니다. 제가 이 부분까지 자세히 파악하지는 못했기 때문에 해당 부분은 논문을 참고해주시기 바랍니다.
Pseudo Code

논문에서 ISM과정에 대해 슈도 코드를 제공합니다.
앞서 SDS에 대해 설명한 내용을 다시 들고와서 조금 고쳐보면
- NeRF 로 특정 view의 이미지를 렌더링 (3)
- DDIM inversion 과정에 따라 timestep 에 따라 렌더링된 이미지에 노이즈를 더함 (4~9)
- pretrained diffusion model의 U-Net에 노이즈 이미지를 넣어 노이즈 예측 (10)
- DDIM Inversion 과정에서 저장한 노이즈 값과 3에서 예측한 노이즈를 이용해 ISM 스코어 계산 및 모델 업데이트 (10~11)
- 모델이 수렴할 때까지(정해진 iter까지) 반복
여기서 , 가 하이퍼파라미터가 사용됩니다.
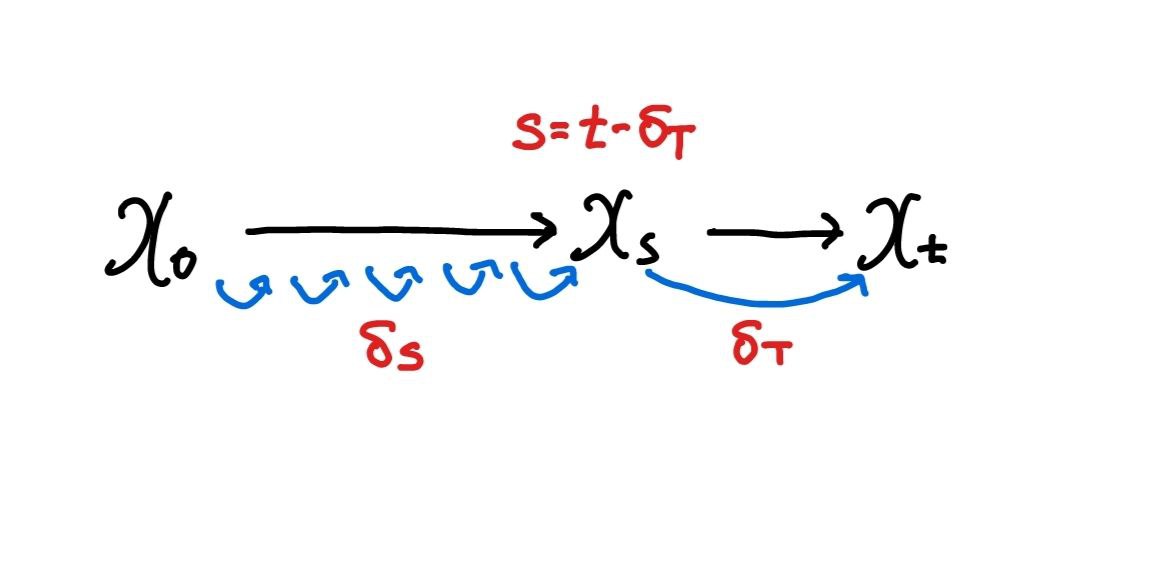
- : 한번에 예측할 timestep 크기
- 클수록 수렴은 빨라지지만 reconstruction error가 증가하여 기존의 SDS처럼 디테일한 부분을 표현하기 어려워집니다.
- 논문에서는 학습 초기에는 큰 로 빠르게 geometry를 포착한 뒤, 를 줄이면서 디테일한 부분을 학습할 것을 권장합니다.
- : DDIM inversion을 얼마나 세분화할 것인지에 대한 파라미터
- 논문에서는 결과에 큰 영향을 주지 않았다고 합니다.
text-to-3D Pipeline
Overall
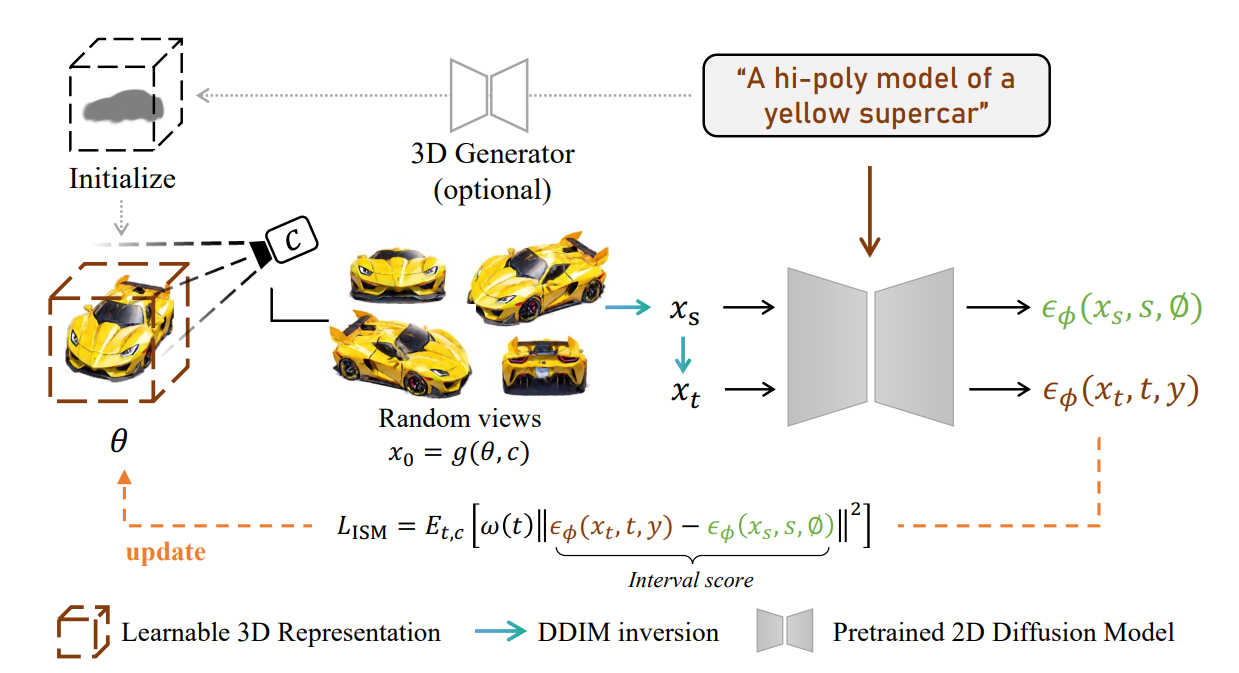
사용되는 loss가 바뀌었을 뿐, 전체 파이프라인의 구조는 변하지 않았기 때문에, 기존 SDS 기반 로직에 쉽게 적용할 수 있을 것이라 생각합니다.
LucidDreamer에서는 NeRF 대신 3DGS를 3D 생성 모델로 사용하여 보다 적은 연산으로 좋은 품질의 렌더링이 가능했다고 합니다.
또한, Open-AI의 text-to-point 모델인 Point-E로 point cloud를 생성하여 3DGS를 initialize했습니다.
그 외에 pseudo-GT를 더 잘 생성하기 위해 Perp-neg, negative prompt와 같은 기법들이 사용되었습니다.
Perp-neg는 Diffusion 모델이 측면, 후면 등의 이미지를 생성할 때 정면 얼굴을 생성하는 경향이 있어 이를 억제하기 위한 기법입니다.
negative prompt 사용에 대해서는 NFSD가 궁극적으로 negative prompt를 통해 SDS 성능을 개선하는 내용이기 때문에 NFSD 논문 리뷰에 어떤 역할을 하는지 설명해둔 것이 있습니다.
그 외에도 3D pipeline에 자유롭게 통합이 가능하기 때문에, 논문에서 사용한 기법 외에도 다양한 시도가 가능할 것 같습니다.
개인적으로 Objaverse 데이터셋을 이용해 3D Prior를 학습한 diffusion model을 적용해보는 것도 품질 향상에 도움이 될 것 같습니다.
Result
text-to-3D는 아직 모델의 성능을 평가할 정량적 지표가 없어 논문에서도 User Study와 같은 정성적 평가만 제공하고 있습니다.
때문에 LucidDreamer 깃허브 페이지에서 제공하는 결과와 속도 정도만 첨부하겠습니다.
렌더링 결과

학습 속도

속도 측면에서는 original DreamFusion과 큰 차이가 없습니다.
DDIM Inversion 및 Point-E 사용으로 연산 자체는 늘었을 것이라 생각하지만, NeRF 대신 3DGS를 사용하여 연산 효율이 증가했다고 합니다.
또한, SDS에서는 10,000 iteration을 학습해야 했지만, ISM을 이용했을 때 수렴 속도가 더 빨라 5,000 iteration 만으로 수렴이 되었다는 점 덕분에 속도 차이가 크게 나지 않은 것 같습니다.
