[논문 리뷰] XLNet: Generalized Autoregressive Pretraining for Language Understanding

preface

1. Introduction

Pretrain의 성공적인 언어 모델 중 2개는 autoregressive (AR) 언어 모델과 autoencoding (AE) 모델입니다. AR 모델은 autoregressive model 능력으로 $X = (x_{1},\dots, x_{T})$ 와 같은 텍스트에, 언어 모델을 구조를 넣은 것입니다. AR 구조는 단방향 학습을 강조하기에 양방향 학습 맥락에는 비효율적입니다. 반면에, downstream language understading task에서는 종종 양방향의 학습 방식이 필요합니다. 그래서 downstream langauge understanding task와 AR 언어 모델과의 pretrain 차이가 발생합니다.

비교를 해보면, AE를 based 한 pretraining은 original data로 부터 없어진 데이터들을 재건축 하는 방식으로 학습을 진행합니다. 대표적인 예시가 BERT입니다. input token이 주어졌을 때, 특정 부분이 MASK화 되어서 대체가 되고, 모델은 그 mask화 된 방식을 복구하는 과정으로 학습이 됩니다. 하지만 이 방식은 실제 데이터가 없어지는 문제를 발생시키기에 discrepancy를 일으킵니다. 거기에 BERT는 joint probability도 사용하지 못하여 서로가 독립이라는 가정하에 unmasked token들 사이의 관계를 예측하면서 학습을 하게 됩니다.

그리하여 저자는 AR모델의 한계성과 BERT 모델이 가지는 단점을 보완하여 XLNet(generalized autoregressive method)를 제안합니다.

다른 기존의 모델과 다른점은

1. 첫번째, 고정된 forward와 backward 분해를 사용하기 보다는, permutation의 factorization order를 사용합니다. 순열 operation 덕분에, 어느 위치에 있든 context는 왼쪽 오른쪽의 모든 토큰들로 구성할 수 있으며, 특히 각 포지션의 맥락적 정보를 활용하는 것을 배우게 됩니다. 이는 즉 bidirectional information을 잡을 수 있는 것입니다.
2. 두번째로, AR 모델을 일반화하기 위해서, XLNet은 Mask를 하는 data corruption에 의존하지 않고, BERT가 만든 unmasked 된 구조에 독립성을 없애려고 합니다.
3. 추가적으로 XLNet은 pretraining하는 모델의 아키텍쳐 디자인 또한 변화시킵니다.
   1. AR 모델에 영감을 받아, XLNet은 segment recurrence mechanism과 relative encoding scheme of Transformer XL 구조를 합쳐서 pretraining에 적용합니다.

위와 같은 과정으로 BERT는 XLNet을 충분히 극복 가능하며, benchmark 학습 기준으로도 높은 성능을 보였습니다.

2. Proposed Method

2.1 Background

이 섹션에서는, 먼저 기본적인 AR 모델과 BERT 구조에 대해서 설명하겠습니다. BERT 구조에 대해서는 이전 블로그에서 다루었으니 저는 AR만 다루겠습니다.

text 데이터가 $X = [x_{1}, x_{2}, \dots, x_{T}]$로 나왔을 때, AR 모델은 likelihood를 최대화하는 구조로 진행이 됩니다.

여기서 $h_{\theta}(\mathbf{x}_{1:t-1})$는 신경망 모델에 의해서 만들어진 context representation이고, $e(x)$는 x의 embedding을 의미합니다. BERT는 AE 모델 중 denoising auto - encoding 모델로 불립니다. 랜덤으로 $x$를 MASK화 하여 그 MASK를 매꾸는 방식으로 학습을 하게 됩니다.

여기서 $m_{t} = 1$을 의미하고, $x_{t}$는 masked, $H_{\theta}$는 Transformer를 의미합니다.

• Independence Assumption
  • BERT는 maksed된 단어들을 제외한 단어들의 독립성을 가정하여 학습을 진행합니다.
  • 하지만 AR 모델은 독립성 가정 없이도 곱셈정리를 사용할 수 있습니다.
• Input noise
  • BERT의 input 구조는 MASK와 같은 인공적인 symbols 들이 들어갑니다. 이는 downstream task에서 볼 수 없는 것으로 pretrain finetune discrepancy를 만들어냅니다.
  • 반대로 AR 구조는 어느 corruption도 하지 않고, 이러한 문제에 대해서 영향 받지 않습니다.
• Context dependency
  • AR representation은 오직 t 조건일 때의 이전 값들로 다 학습을 진행을 하는데, BERT는 양 사이드에서 맥락적 정보를 가지고 있습니다. 결과적으로 BERT는 모델이 bidirectional 정보를 다 읽을 수 있게 도와줍니다

2.2 Objective : Permutation Language Modeling

위를 정리해보면 AR구조와 BERT는 각각의 장점을 가진다. 그리하여 저자는 각각 그들의 강점을 최대한 살리고 단점을 버리는 구조로 XLNet을 만든다.

그래서 저자는 permutation language modeling 구조를 제안한다. 이는 AR 모델의 장점을 보유하고 있으면서도 양방향의 정보를 읽을 수 있는 것이다. 특히 sequence $\mathbf{x}$, 문장 길이는 $T$를 다룰 때, 총 문장의 수는 $T!$으로, 유효한 AR의 분해 구조를 구할 수 있다. 직관적으로도 만약 모델의 파라미터들이 모두 유효한 순서로 나뉘어져 있으면, 모델은 모든 position에서 양방향으로 정보를 모을 수 있게 됩니다.

예를 들어서 T=4이면 24개로 [1,2,3,4], [1,2,4,3], [1,3,2,4], [1,3,4,2],[1,4,2,3],[1,4,3,2]…,[4,3,2,1]로 24개의 데이터를 input data에 넣게 되고 이것이 $z$를 의미합니다.

이러한 생각을 수식으로 정리해보면, 일단 $z_{t}$와 $\mathbf{z}_{<t}$로 t번째 element와 t-1번째의 모든 permutation 과정을 가르쳐줍니다. 그리고 구조화된 식은 아래와 같습니다.

t번째 이전까지의 모든 값들이 나왔을 때의 확률 값이 가장 크게 하는 구조로, Permutation의 특성 상, 순서가 있기 때문에 Bidirectional 정보 또한 읽을 수 있습니다.

Remark on Permutation

고안된 방법은 factorization order뿐만 아니라 sequence order까지 계산을 하기 때문에 이는 positional encoding을 이용하여 순서화했다고 볼 수 있습니다. fine tuning 동안 자연적 순서와 관련된 text sequence들만을 마주치기 때문에, 이러한 선택은 필수적이라고 볼 수 있습니다.

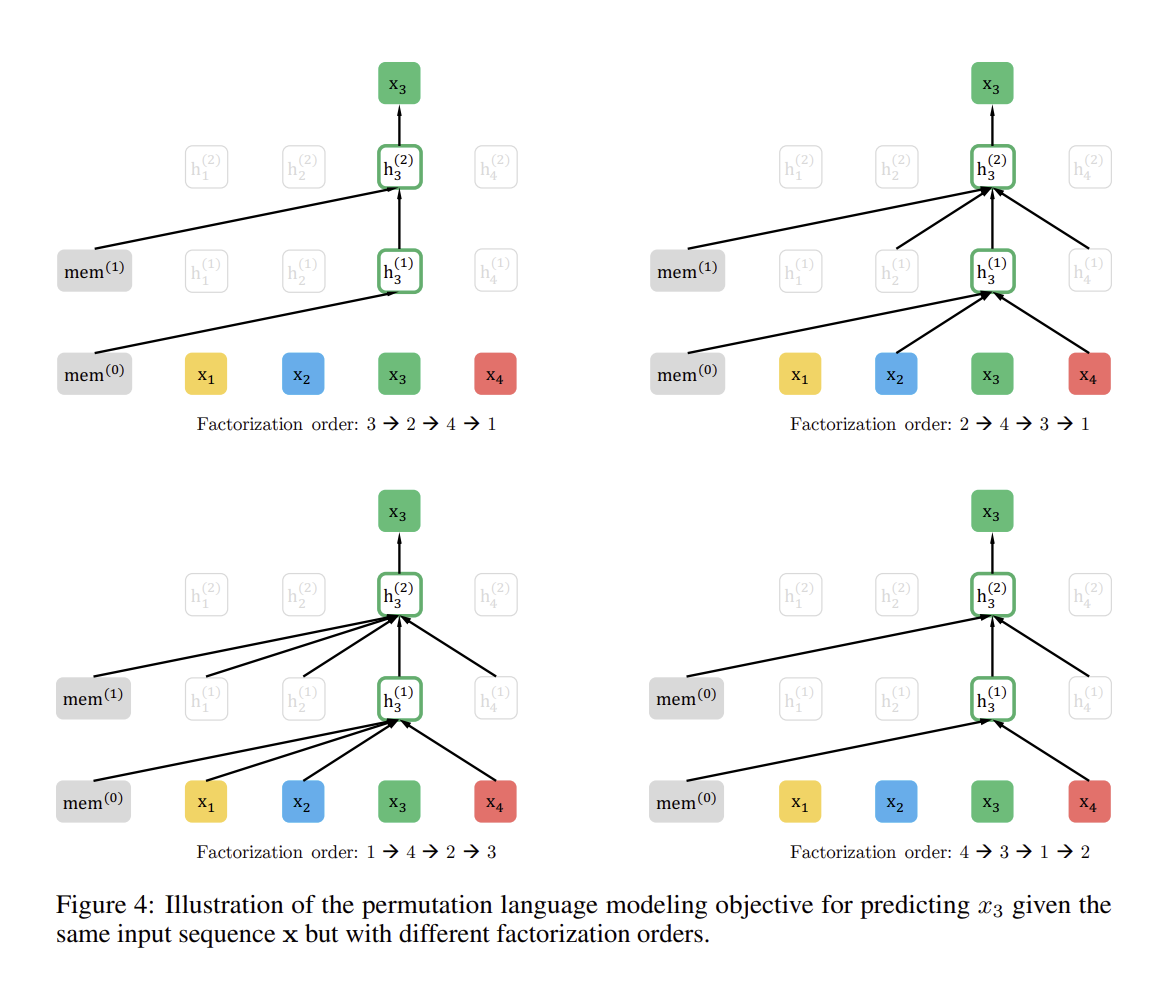
위 그림을 확인해보면, $x_{3}$를 학습하는데 있어서, 경우의 수가 각각 다른것을 확인할 수 있습니다.
하지만 뒤에 논문을 읽게 되면, 이 방법을 써서는 기본적인 Transformer 구조는 전혀 못씁니다. 절대적인 positional encoding을 사용하는 방식에서 permutation으로 계속 위치가 바뀌다 보니 절대적인 위치라는 개념이 사라집니다. 그래서 relative position을 강조하면서 논문이 전개가 됩니다.

2.3 Architecture : Two - Stream Self - Attention for Target - Aware Representations

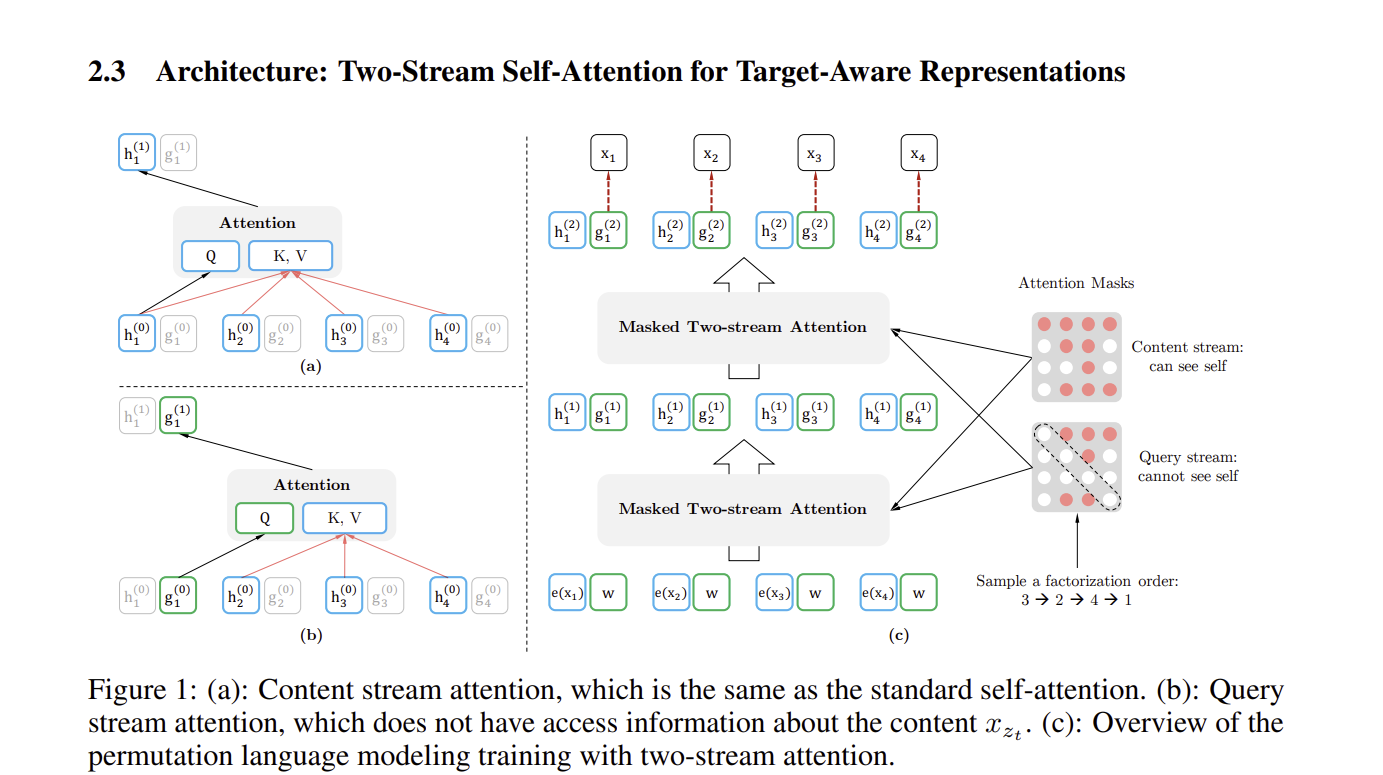
위 그림에서 (a)는 stream ateention을 의미하는 것으로, self attention과 비슷합니다.

앞에서 말한 permutation 구조를 사용하는 것은 바람직하지만, 이 구조를 사용하면 표준 Transformer를 사용하지 못할 수도 있습니다. 문제의 핵심은 표준 Transformer의 다음 토큰 분포인 $p_{\theta}(X_{z_{t}}|\mathbf{x}_{z<t})$를 사용할 때 입니다. 이는 아래와 같이 쓸 수 있습니다.

여기서 중요한 점은 $h_{\theta}(\mathbf{X}_{z<t})$이 $\mathbf{x_{z<t}}$의 hidden representation을 의미하는 것으로, 이는 Transformer network가 maksing 이후에 만들어지는 것입니다. 그래서 이와 같은 representation은 어느 표지션에 있는지를 예측하는데는 전혀 사용되지 않습니다. 다시 말해서, $z_{t}$ 같은 값 말이죠. 그래서 target position과는 전혀 관계없이 같은 분포만 계속적으로 예측이 됩니다. (쓰면서도 이 문장이 이해가 잘 안가서 Transformer의 구조를 정리하면서 다시 보겠습니다.)

<왜 Transformer 모델은 $Z_{t}$를 예측하는데 전혀 안쓰일까?>

Transformer의 기본 설정에서는 각 토큰의 위치에 대한 정보가 포함되지만, 이 정보는 주로 해당 토큰의 임베딩에 포함되어 있으며, self attention 계산 과정에서 토큰이 위치한 특정 시점에 대한 정보는 직접적으로 사용되지 않습니다. 즉, 특정 위치에 대한 정보는 해당 위치에서 무엇을 예측해야 하는지에 대한 직접적인 지시로 사용되지 않습니다. 즉 문장이 특정 시점에 어디 위치해있는가 보다는 어느 문장과 어느 문장이 직접적으로 관련이 있는지 만을 확인하는 용도이기 때문에 $z_{t}$가 안쓰인다고 볼 수 있습니다.

그래서 이러한 문제를 해결하기 위해서 저자는 새로운 구조를 제안합니다.

Two - Stream Self - Attention

여기서는 $g_{\theta}(\mathbf{x}_{\mathbf{z}<t},z_{t})$을 어떻게 만드는지에 대해서 말해줍니다. 저자는 target position에서 ‘stand’를 정의합니다. 이를 위해서는 기존의 Transformer 구조에서 2가지의 추가적인 정보가 필요합니다.

1. $\max \log p_{\theta}(\mathbf{x}) = \sum_{t=1}^{T}\log p_{\theta}(x_{t}|\mathbf{X}{<t}) = \sum{t=1}^{T}\log \frac{\exp(h_{\theta}(\mathbf{x}{1:t-1})^Te(x{t}))}{\sum_{x'}\exp(h_{\theta}(\mathbf{x}_{1:t-1})^Te(x'))}$ 식을 정리하기 위해서는 $z_{t}$를 쓰고, $x_{t}$를 사용하면 안됩니다.
2. $\max \log p_{\theta}(\mathbf{x}| \tilde{\mathbf{x}}) \approx \sum_{t=1}^{T} m_{t}\log p_{\theta}(x_{t}|\mathbf{\tilde{x}}) = \sum_{t=1}^{T}\log m_{t} \frac{\exp(H_{\theta}(\mathbf{\tilde{x}})^Te(x_{t}))}{\sum_{x'}\exp(H_{\theta}(\mathbf{\tilde{x}})^Te(x'))}$ 식을 정리하기 위해서는, $g_{\theta}$는 $x_{z_{t}}$를 encode 해야 합니다.

이러한 문제점을 해결하기 위해서, 저자는 2가지의 방식을 제안합니다.

• content representation을 해주는 $h_{\theta}(\mathbf{x}_{\mathbf{z}<t})$은 context와 $x_{z_{t}}$ 를 encode하고,
• query representation을 해주는 $g_{\theta}(\mathbf{x}_{\mathbf{z}<t}, z_{t})$ 값은 contextual information $\mathbf{x}_{z<t}$와 position $z_{t}$을 가지고 있어야 합니다.

이를 통해 이제 자신의 위치에 대한 학습이 가능해집니다. 업데이트는 다음과 같습니다

Partial Prediction

Permutation language modeling에서 이점을 가지는 동안, permutation때문에 생기는 최적화 문제와 이전의 실험에서 나온 느리게 수렴하는 문제등을 해결해야 합니다. 최적화를 쉽게 하기 위해서, 저자는 마지막 토큰을 오직 predict를 하는데 사용합니다. $z$를 non target subsequence $\mathbf{z}_{\leq c}$와 target subsequence $\mathbf{z}_{>c}$로 나눕니다. 이 실험의 목표는 non target 데이터를 전제로 하여 target 데이터의 log likelihood를 최대한 크게 하는 것입니다.

이렇게 하면 c+1 부터 선택이 되어, 문장에서 가장 긴 context를 보유할 수 있습니다.

2.4 Incorporating Ideas from Transformer - XL

Transformer XL의 relative positional encoding scheme과 segment recurrence mechanism을 합쳐서 XLNet에 넣었습니다. relative positional encoding scheme은 위에서 붙였기 때문에 segment recurrence mechanism을 고민해봅시다. WLOG로, 2개의 segment가 있다고 가정을 합니다. $\tilde{x} = \mathbf{s}_{1:T}, \mathbf{x} = s_{T+1: 2T}$ 라고 합시다. 그 다음에 $\tilde{z} ,z$ 두 개를 각각의 permutation이 되어싿고 가정을 했을 때, tilda permutation은 첫번째 segment로 진행하고, $\tilde{h}^{m}$의 content representations을 얻게 됩니다. 그 다음 그냥 permutation에서 이를 가지고

$h^{(m)}{z_t} \leftarrow \text{Attention}\left(Q = h^{(m-1)}{z_t}, KV = \begin{bmatrix} \tilde{h}^{(m-1)} \\ h^{(m-1)}_{z \leq t} \end{bmatrix}; \theta \right)$ 이렇게 업데이트를 진행해줍니다. 여기서 업데이트는 $\tilde{z}$와는 독립적이라는 것을 알아야 합니다.

2.5 Modeling Multiple Segments

많은 downstream task들은 여러 개의 input segment가 있습니다. 이제는 어떻게 XLNet을 pretrain 할 것인지에 대해서 알아봅시다. BERT와 비슷하게, 2개의 segment를 샘플링하고, 두 개를 하나의 sequence로 붙여줍니다. 특히, 모델의 input data는 BERT와 구조가 같습니다[CLS, A, SEP, B, SEP]입니다.

Relative Segment Encodings

구조적으로 BERT와 다른 것은 Transformer XL을 통한 relative encoding을 했다는 점입니다. i와 j번째 단어가 있는 sequence가 주어졌을 때, 만약에 같은 segment에서 이들이 왔다면 segment encoding을 $s_{ij} = s_{+}$로 쓰고, $s_{ij} = s_{-}$라고 씁니다. 핵심은 i번째 값이 만약에 j번째 값한테 간다면, 이를 계산하는 attention weight가 나오게 됩니다. 그러고 나서, value $a_{ij}$는 normal attention weight에 더해집니다. 이러면 2개의 장점이 있습니다. 첫번째로, relative encoding의 inductive bias는 일반화 성능이 올라가고, 두번째로 2개 이상의 input segment에 fine tuning을 하는 가능성도 또한 열어줍니다.

2.6 Discussion

이번 섹션에서는 [New, York, is, a, city] 라는 문장을 BERT와 XLNet을 통해서 어떻게 처리되는지를 보여줍니다. 먼저 [New, York] 2개의 단어의 확률을 구하고 싶을 때, 우리는 $\log p(New \ York | \ is\ a\ city)$라는 확률을 최대화 하고 싶어합니다.

BERT와 XLNET 각각 학습 구조는 다음과 같습니다

그래서 XLNet은 New와 York 사이의 dependency도 계산이 가능해집니다.

3. Experiments

3.1 Pretraining and Implementation

XLNet-Largesms BERT-LARGE와 똑같은 하이퍼 파라미터를 가지고 ㅣㅆ으며, 모델 사이즈 결과도 ㅣ슷하다.

3.2 Fair Comparision with BERT

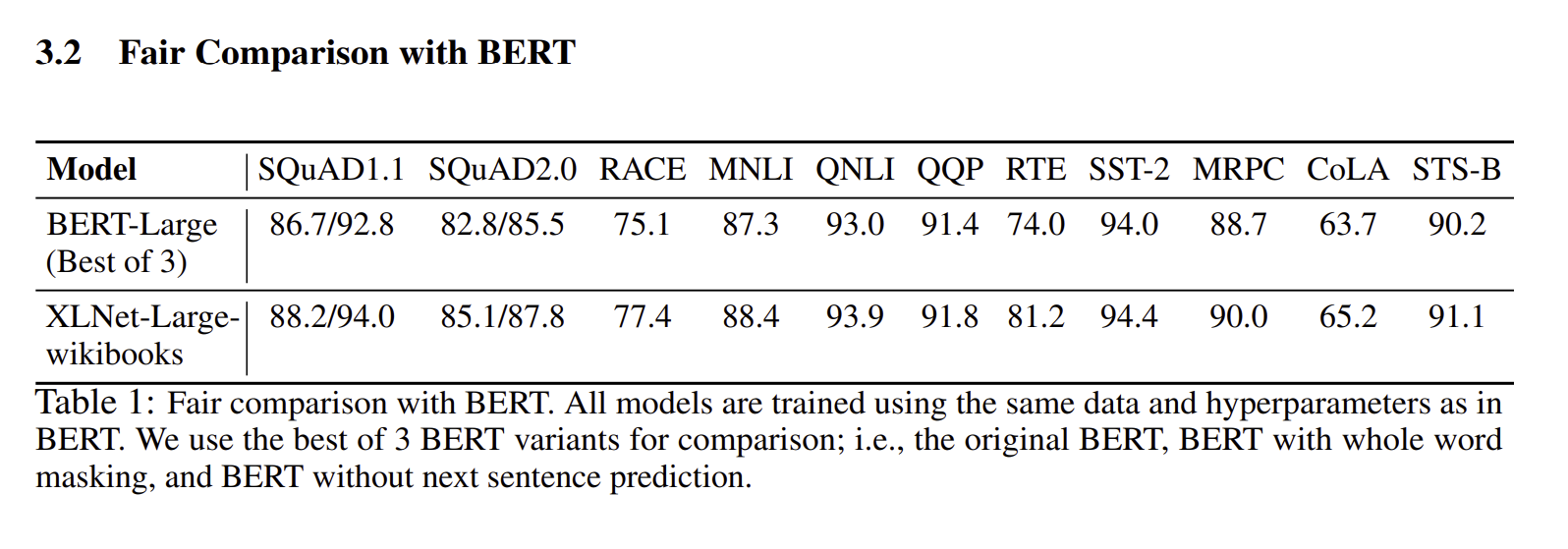
benchmark의 전체적인 성능을 비교해보면 확실히 XLNet-LARGE가 더 높은 성능을 보여줌을 알 수 있다.

3.3 Comparison with RoBERTa : Scaling up

당시 SOTA였던 RoBERTa 보다 더 높은 성능을 보였다.

4. Conclusion

XLNet은 permutation language modeling을 활용하는 AR와 AE의 장점만을 모아둔 AR pretraining 방식이다.

한줄로 요약하면?

XLNet은 permutation을 통해 양방향 position context를 찾고 AR 기능을 유지한 자연어처리 모델입니다.