[기계학습] Dimensionality Reduction(Non-Linear)

From Subspace to Nonlinear Manifold

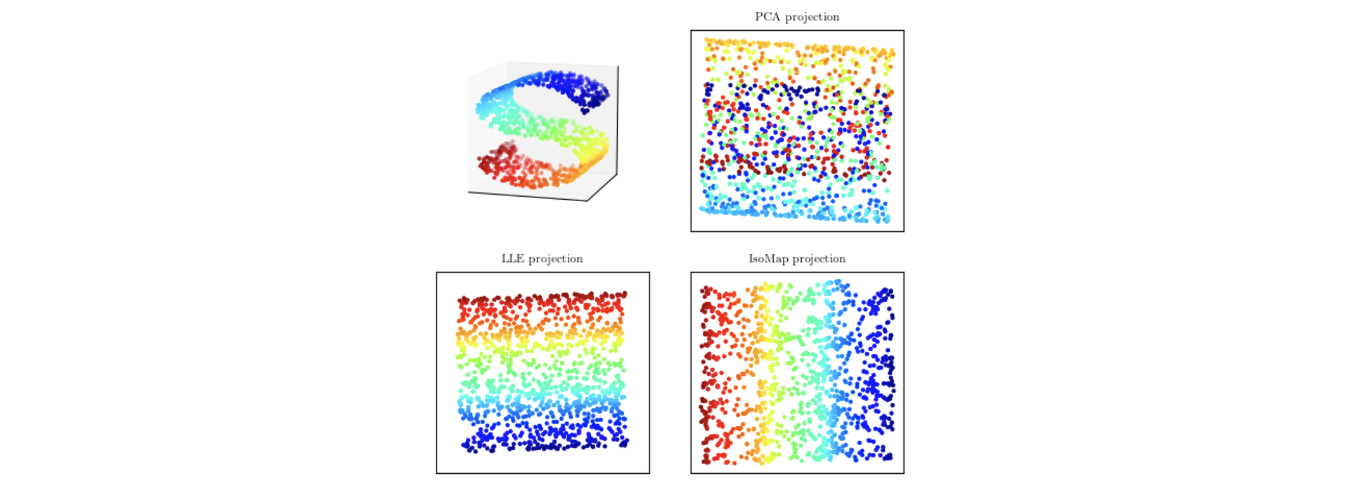위와 같이 S 모양의 data가 3차원 상에 존재한다고 해보자. 그러면 PCA가 3차원의 data를 2차원으로 줄여줄 것이다. 그러면 우상단과 같은 projection 결과가 만들어 질 것이다. 원래의 manifold에서는 data가 색깔에 따라서 확실하게 구분이 되었지만, 이를 PCA projection 시키게 되면 모든 것이 linear projection이기 때문에 겹치는 상황을 피할 수 없게 된다. 특정 방향으로 projection 시킨다면 red와 blue data는 확실하게 구분할 수 있겠지만, 중간에 존재하는 다른 색의 data는 결국에는 겹치게 될 것이다. 그래서 이러한 문제를 해결하고자 non-linear PCA에 대해서 알아볼 것이다. 이는 그리 어렵지 않고 3차원의 data point를 그저 어떠한 plane 혹은 space에 projection시킬 것이다.

Kernel PCA(KPCA)

A Famous Example of Nonlinear Dimensionality Reduction

앞서 이야기했듯이 기존의 manifold에 있는 data를 다른 어떠한 manifold로 이동시킬 nonlinear mapping을 찾을 것이다. 다음은 nonliner dimensionality reduction의 필요성을 느끼게 해줄 또다른 예시이다.
위와 같이 두 종류의 data distribution이 있을 때 linear dimensionality reduction을 하게 되면 중간과 같은 결과를 얻게 될 것이다. 그러나 이러한 결과를 가정했을 때 2차원의 data point에 대한 mapping function을 $\phi(x_1,x_2)=(x_1,x_2,x_1^2+x_2^2)$와 같이 정의할 수가 있다. 여기에 data point의 norm을 추가로 도입했다. 그러면 이러한 feature extractor를 사용했을 때 불행하게도 더 높은 차원을 도입하게 된다. 원래의 space가 2차원이라면 feature space는 3차원의 공간이 되는 것이다. 그러나 만약 추가적인 차원을 포함하고 동일한 linear PCA를 적용할 수 있다면 우측의 결과와 같이 꺠끗하게 data가 분리될 것이다. 왜냐하면 blue circle의 data point가 작고 red circle의 data point가 큰 값을 가진다면 추가적인 차원의 feature space에서 효과적으로 정보를 압축할 수가 있다.

Objective in Kernel PCA

Kernal PCA에서 non-linear mapping $\phi$가 주어지게 되고, feature extractor로 여겨진다. $\phi$는 원래의 $D$차원에서 $D'$차원으로 mapping 시켜주지만 이전과는 다르게 $D'$ 차원이 $D$차원보다 작을 필요가 없다. 커도 되고 같아도 되며 작아도 상관이 없다. Kernel PCA는 정보의 손실을 최소로 만드는데 목적을 두고 있다.

이러한 과정은 결국 feature가 정규화 되었다는 가정 하에 covariance matrix로부터 $N$개의 가장 큰 eigenvector를 찾는 것과 같다. Feature 혹은 data point의 합이 0이라는 것이 가정이다. 이러한 가정은 notation을 간단하게 만들어준다.

PCA in Feature Space

이전의 PCA에서는 eigen value와 eigen vector를 찾는 것이 목적이었다. Eigen vector $u_i$는 orthonormal vector이고 간단한 조작을 통해서 $u_i$를 $x$의 weighte sum으로 나타낼 수 있었고, weight는 $\alpha$로 나타냈었다. 이전에 봤던 이러한 관점으로 kernel PCA에서도 적용될 수 있다.

Nonlinear mapping $\phi: R^D\mapsto \mathcal{F}(\text{feature space)}$에 대해서 $\sum_{n=1}^N \phi(x_n)=0$ 을 가정하면 다음과 같이 featuer space $\mathcal{F}$에서 covariance matrix $\bar{S}$를 정의할 수 있다. 0 mean을 가정하는 이유는 만약 0 mean이 아니라면 각 $\phi$마다 평균을 빼주는 복잡한 식을 사용해야 한다.

그러면 feature space에서 PCA는 다음을 풀어야 한다.

결국 각각의 orthogonal vector $v_i$를 다음과 같이 구할 수가 있다.

각 $v_i$는 feature vector의 weighted sum으로 나타낼 수 있게 된다. 따라서 kernal PCA 문제를 풀기 위해서 $\{\alpha_{in}\}'s$를 찾을 것이다. $\alpha$ 값들만 구하면 모든 것을 구할 수가 있게 된다.

Kernel Matrix

Nonlinear mapping $\phi$를 가정하게 되면 kernel PCA는 $\alpha_{in}$찾는 과정이 된다. 그래서 최종적으로는 reduced feature space로 이동시키는 $V$를 찾게 되는것이다. $\alpha_{in}$을 찾기 위해서 먼저 kernel matrix $K \in R^{N\times N}$를 정의해야 한다. Kernel matrix는 data point들 사이의 distance를 나타내는 것이다.

이러면 kernel matrix는 symmetric하고, $v_i=\sum_{n=1}^N\alpha_{in}\phi(x_n)$을 이용해서 $v_i$에 대한 eigenvalue equation을 다음과 같이 나타낼 수 있다.

양변에 $\phi(x_l)^T$를 좌측에 곱해주고 $k(x_n,x_m)=\phi(x_n)^T\phi(x_m)$ 이라고 정의하게 되면 다음과 같은 결과를 얻을 수 있다.

Column vector $\alpha_i = [\alpha_{i1},\dots,\alpha_{iN}]^T$이라고 했을 때, 다음과 같이 정리할 수 있다.

Equivalent Eigenvalue Equation with Kernel Matrix

위의 식은 원래의 공간에서 eigenvalue equation과 같고, 그래서 다음과 같이 더 간단해 질 수 있다.

단순히 $K$를 하나씩 지운 것이다. 두 방정식은 principal components projection에 영향을 미치지 않는 eigenvalue가 0인 $K$의 eigenvector에 의해서만 다르기 때문이다. 즉, 0이 아닌 $\lambda_i$의 $\lambda_i N\alpha_i = K\alpha_i$에 대한 솔루션은 $\lambda_iNK\alpha_i=K^2\alpha_i$가 되어야 한다. 여기서 $\lambda_i N$는 scalar 값이고 $K$는 vector이다. 그래서 또다시 kernel matrix에 대한 eigenvalue decomposition을 한 것이다.

Eigen value equation을 바로 사용하기 보다 kernel matrix가 등장하게 된 이유는 kernel function을 사용하면서 computational cost를 줄일 수 있기 때문이다.

Normalization in Kernel PCA

완전한 PCA를 위해서는 normalization 과정이 필요하다. $v_i$는 unit vector로 만들어야 해서 다음과 같이 $\alpha_i$에 대한 constraint로 해석될 수 있다.

즉, KPCA는 다음을 만족하는 $\alpha_i$들을 찾게된다.

Compute Nonlinear Components

우리가 필요한 것은 feature보다 kernel을 정의하는 것이다. 그래서 지금까지의 내용들은 명시적으로 feature function의 표현에 대해서는 필요로하지 않는다. Feature map $\phi$가 명시적으로 표현될 필요가 없었다. 대신 2개의 data point를 비교하는 kernel function을 나타낼 수 있었고, 이거면 충분하다.

Linear PCA에서는 principal component들이 covariance matrix S의 eigenvector $u_i$ 위로 data $x$를 projection 시키면서 얻을 수 있었다.

Kernel PCA에서도 data $x$를 $\bar{S}$의 eigenvector $v_i$ 위로 projection 시킬 수 있다.

Centering in Feature Space

다음은 centered feature 가정을 배제하고 kernel PCA를 계산하는 구체적인 algorithm이다. 현실에서는 이러한 centered feature를 얻지 못할 것이다. 완전히 설명하기 위해서 kernel PCA algorithm는 centered kernel matrix $\tilde{K}$로 시작한다. 그래서 $\tilde{K}_{nm} = \langle \tilde{\phi}(x_n), \tilde{\phi}(x_m)\rangle$ 은 $x_n,x_m$의 centered feature의 inner product가 되고, 여기서 centered feature는 다음과 같이 정의된다.

이 정의로부터 centered kernel matrix를 다음과 같이 다시 적을 수 있다.

$K_{nm}$은 center를 제외한 kernel이고 이를 통해서 centered kernel matrix $\tilde{K}$를 uncentered kernel matrix $K$로 다음과 같이 나타낼 수 있다.

Summary of KPCA

그러면 다음과 같이 kernel PCA 과정을 정리할 수 있다.

1. Prepare: 먼저 kernel matrix $K\in R^{N\times N}$를 구하고 centered kernel matrix $\tilde{K}$를 계산한다.
   $\tilde{K}=K-1_NK-K1_N+1_NK1_N$
2. KPCA: $\tilde{K}$가 정의되면 다음과 같은 eigenvalue problem을 정의할 수 있고 풀어야 한다.
   $N\lambda_i\alpha_i=\tilde{K}\alpha_i$
   이로부터 $\alpha_i$를 찾으면 다음과 같이 $\alpha_i$를 정규화를 시켜준다.
   $\|\alpha_i\|^2=\frac{1}{N\lambda_i}$
3. Use KPCA: 새로운 data $x$에 대해서 다음과 같이 nonlinear component를 얻을 수 있다.
   $\langle v_i, x\rangle = \sum_{n=1}^N\alpha_{in}k(x_n,x)$
   그러면 새로운 data $x$에 대해서 reduced expression이 생기게 된다. 이 과정에서 $D$차원의 computation을 필요로 하지 않는다. 대신에 모든 것이 kernel function $k$에 의해서 설명이 된다. 그래서 feature의 차원보다는 data 개수인 $N$에 관해서 computation time이 바뀌게 된다.

Example of KPCA

다음은 2006년에 Ghodsi가 제공한 kernel PCA의 예시이다.
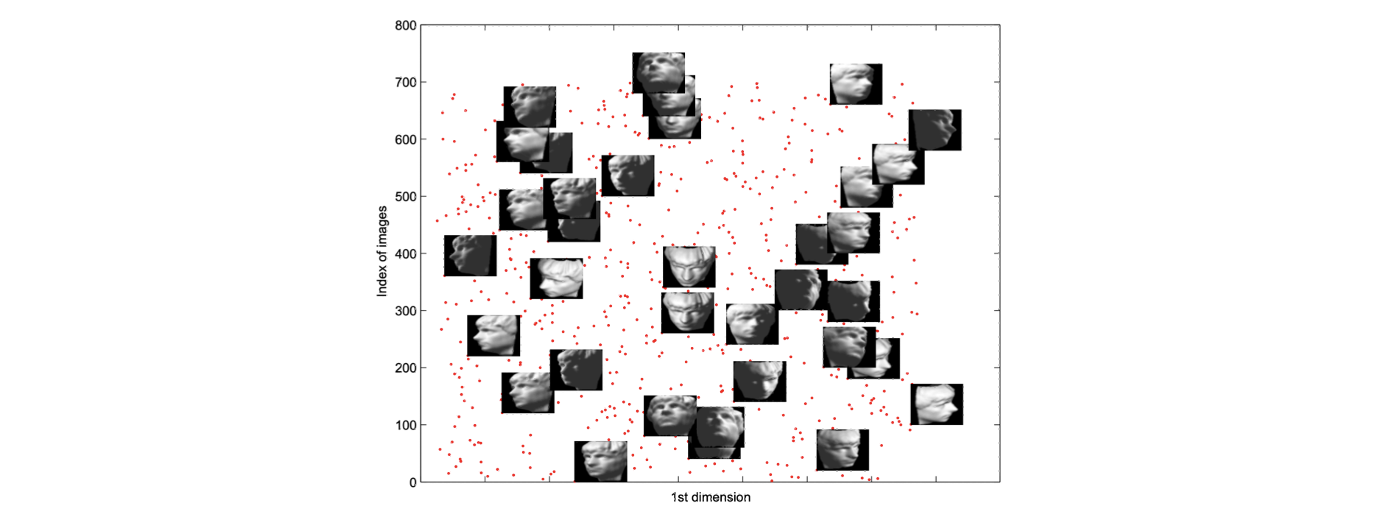각 data point가 얼굴 조각상 image라고 했을 때 위의 plot은 1차원에서 image index를 나타내고 있다. 보다시피 서로 상관관계는 많이 없어보이지만 위의 plot을 세로로 3등분 하게되면 가장 우측은 오른쪽 얼굴이 보이고 가장 좌측은 왼쪽 얼굴이 보이고 나머지 중간부분은 정면을 보고 있다. 그러나 사실 이것은 잘 정리된 것이 아니다.

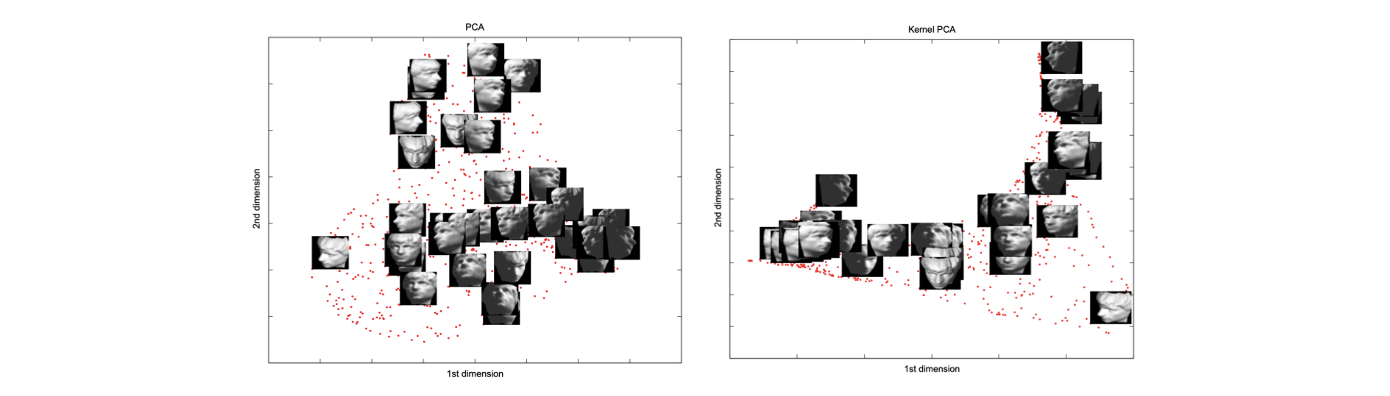Linear PCA나 kernel PCA를 이용하면 cluster 형성이 더 자연스러운 결과를 만들어낸다. 그러나 완벽한 것은 아니다. 좌측의 linear PCA를 보면 2차원의 PCA 결과인데 대략 clustering 결과는 좋으나 완전히 다른 결과도 보이고 있다. 사실 얼굴의 방향을 보면 다르지만 밝기의 관점에서 본다면 clustering 결과가 자연스럽다. 그러나 이는 원하는 결과는 아니다. Kernel을 잘 정의하고 KPCA를 진행하게 되면 우측과 같이 얼굴의 방향대로 clustering 결과가 좋은 것을 볼 수 있다. 우측의 결과는 밝기의 관점에서는 잘못된 결과이다. 이렇게 kernel을 잘 정의하게 되면 좋은 결과를 만들 수 있다.

Other Nonlinear Dimensionality Reduction

Nonlinear dimensionality redectuion의 또 다른 예시를 보도록 하자.
KPCA에서도 보았지만 두 data point 사이의 distance를 정의하는 것이 정말 중요하다. 여기서 살펴볼 isomap은 data point의 graph를 만들어내고, 가장 가까운 pair를 연결시켜 준다. 이렇게 graph 구조를 가지고 이 graph에서 2개의 data point의 거리로서 kernel을 정의하는 것은 성공적인 dimensionality reduction을 가능하게 했다.

A로부터 가장 가까운 data를 모두 연결하게 되면 B와 같은 결과를 얻을 수 있다. 이는 다시 C와 같이 2차원에서 visualization 될 수 있다. 그러면 2개의 data point 사이의 distance를 새로 정의할 수 있다. 원래의 space에서 직관적으로 가깝다고 생각되는 point들이 isomap에서는 실제로 먼 distance를 가지게 된다. 이를 이용하면 정보의 손실을 줄이면서 dimensionality reduction을 더 성공적으로 할 수 있다.

여기서 다루는 모든 dimensionaltiy reduction에서 distance metric이나 kernel function을 잘 정의할 필요가 있다. 사실 이러한 과정은 어렵고 복잡한 일이다. 그래서 automated approach를 사용하면 이러한 복잡한 일을 하지 않아도 된다.

Feedforward Auto-Encoder in Neural Network

현실에서는 kernel function이나 feature function 등이 주어지지 않는다. 그래서 이를 찾기 위해서 auto-encoder 등을 사용해야 한다. 복잡하게 metric이나 function을 정의하지 않아도 되는 방식으로 하나하나 알아보겠다.

Encoder

Encoder는 data $x \in R^D$를 고차원의 data를 요약한 latent feature $z \in R^M$으로 mapping하는 일종의 dimensionality reduction function이다. 여기서 $D >> M$이라고 가정한다. PCA는 이러한 encoder의 선택을 제공해주지만 우리가 실제로 원하는 것은 자동으로 encoder를 선택하는 것이다. 그래서 이러한 부분에 초점을 둘 것이다.
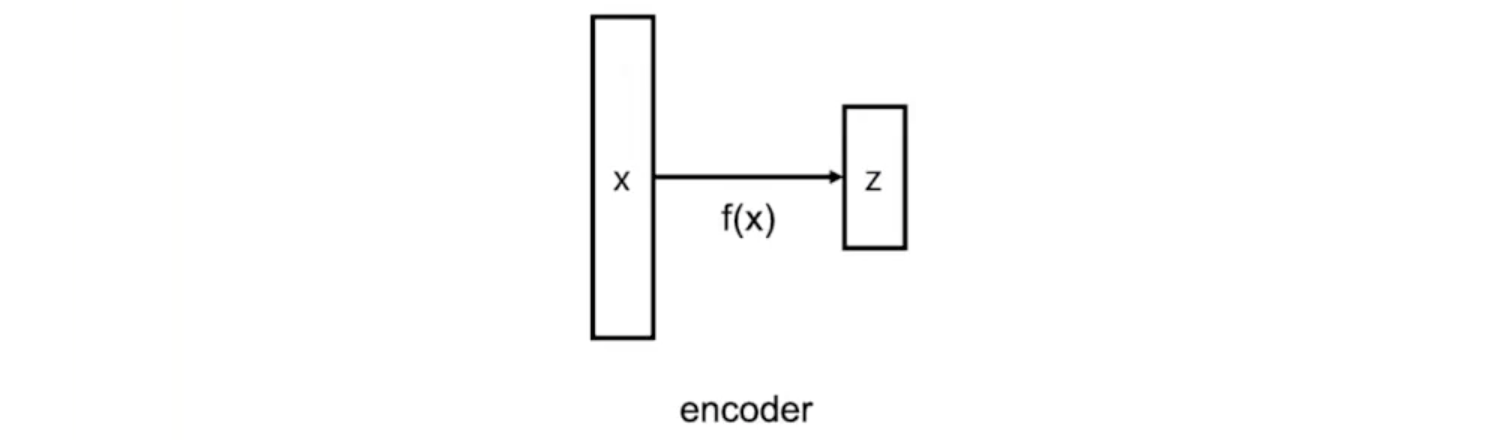우리는 기존의 data point를 차원을 줄여주는 latent feature에 encoding 하는 것이 목적이다. 그래서 machine learning 연구자들은 어떻게 이러한 function $f$를 학습시키고 이 function으로부터 무엇을 얻기를 원하는지 생각했다. 그래서 여러 input만 넣으면 되는 machine learning approach를 생각했고 encoder가 잘 만들어지면 이를 만족시킨다는 것을 알았다.

Autoencoder

이를 위해서 auto-encoder를 생각할 수 있고 이는 encoder와 decoder가 합쳐진 구조로 생겼다. 원래는 encoder가 필요하지만 encoder와 decoder를 가지는 이유는 encoder의 설명이 다음과 같기 때문이다.

우리가 원하는 것은 data $x$의 대부분의 정보를 가질 수 있는 latent feature $z=f(x)$이다. 일단 $z$가 대부분의 정보를 가질 수 있다면 latent feature $z$로부터 data $x$를 복원할 수 있게 된다. 이를 기반으로 auto-encoder 구조를 생각할 수 있으며 여기서 encoder는 data point를 요약하려고 시도하고 decoder는 latent feature로부터 data를 복원하는데 초점을 두게 된다.
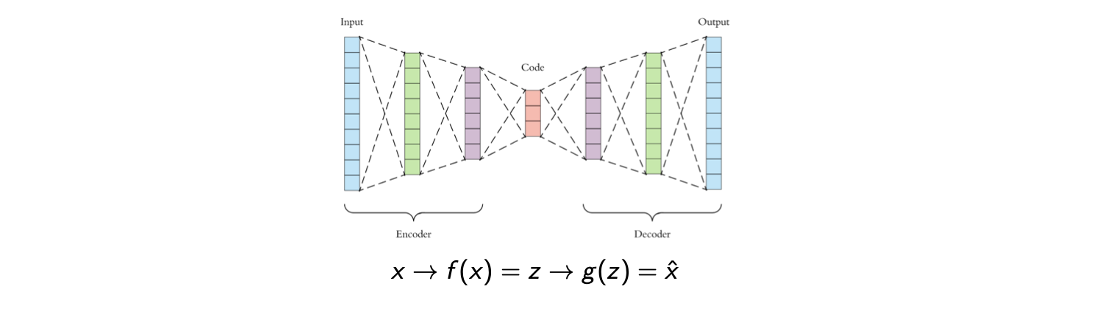이렇게 auto-encoder를 구성하면 data를 압축하고 복원할 수 있게 된다. 학습의 목표는 loss fuction을 최소로 만드는 것이고, loss function $d(x,g(f(x)))$은 원래의 data와 복원시킨 data 사이의 distance 비교하게 된다. 대표적으로 L2-norm을 사용할 수 있다. 이를 self-supervised learning 기법이라고도 부르는데, 그 이유는 오로지 data point $x$만을 가지게 되고, $x$만으로 supervised learning frame을 만들수 있기 때문이다. 그렇다면 이러한 구조는 어떻게 동작하는 것일가?h

A Typical Choice of f and g for Image

Encoder $f$는 기존의 많이 봐왔던 것 처럼 convolution을 수행하지만, decoder $g$는 transposed-convolution을 수행하게 된다.
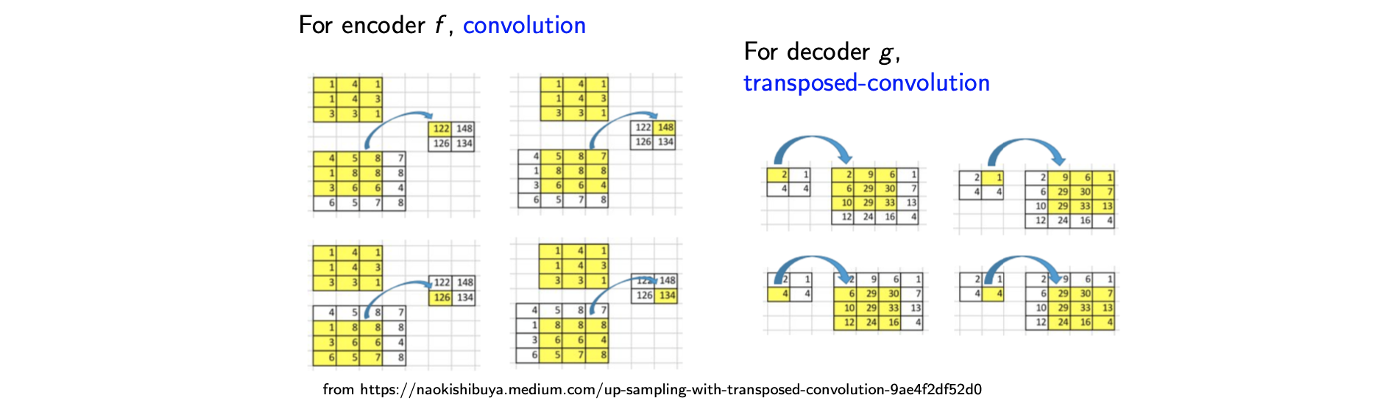Encoder에서 이러한 방식이 image에서 효과적인 이유는 image가 spatial correlation을 가지기 때문이다. 이웃하는 pixel들의 관계를 자세히 보면 해당 image를 복원할 수 있다는 것이다. 그래서 예전부터 convolution을 주로 사용해왔던 것이다.

Padding을 하지 않고 convolution을 하고나면 dimensionality reduction 결과를 보게될 것이다. 그래서 위와 같이 $4\times 4$ image에 $3\times 3$ filter를 사용하면 $2\times 2$ image를 가지게 된다. 이렇게 줄어든 image를 이용해서 decoder는 transposed-colvolution을 수행한다. 줄어든 image에 convolution에서 사용된 filter를 다시 사용하게 되는데 역으로 생각해서 image를 채워나가면 된다. 그러면 결과적으로 image를 복원할 수 있다.

An Application of Autoencoder: Semisupervised Learning

Auto-encdoer 구조를 만들고 학습시키는 것을 여러 분야에 적용할 수 있다. 한가지는 이 자체로 사용해서 dimensionality reduction을 하고 data space를 저장하는 것이다. 그래서 data compressor와 decompressor로 생각할 수 있다. 이보다 더 흥미로운 것으로 semi-supervised learning을 auto-encoder의 application으로 생각할 수 있다. Semi-supervised dataset에 대해서 image classification task를 수행하고 싶다고 해보자. Semi-supervised dataset은 일부 data는 label을 가지고 있고, 나머지는 가지지 않은 dataset을 말한다. 이는 실제로 어디서든 사용이 가능하다. 왜냐하면 labeling task는 사람의 시간과 돈을 필요로 하는데 실제로 한계가 존재하기 때문이다. 그래서 우리는 종종 unlabeled dataset을 labeled dataset에 비해서 훨씬 많이 가지게 된다. 이러한 상황에서 오로직 labeled data에 대해서 학습하고자 하지만 unlabeled dataset도 dataset이 가지는 어떠한 pattern이 존재한다고 생각해서 이를 이용하고자 한다. 그래서 등장한 것이 semi-supervised learning이라고 한다. 다음은 이러한 방법이 가지는 장점을 보여주고 있다.

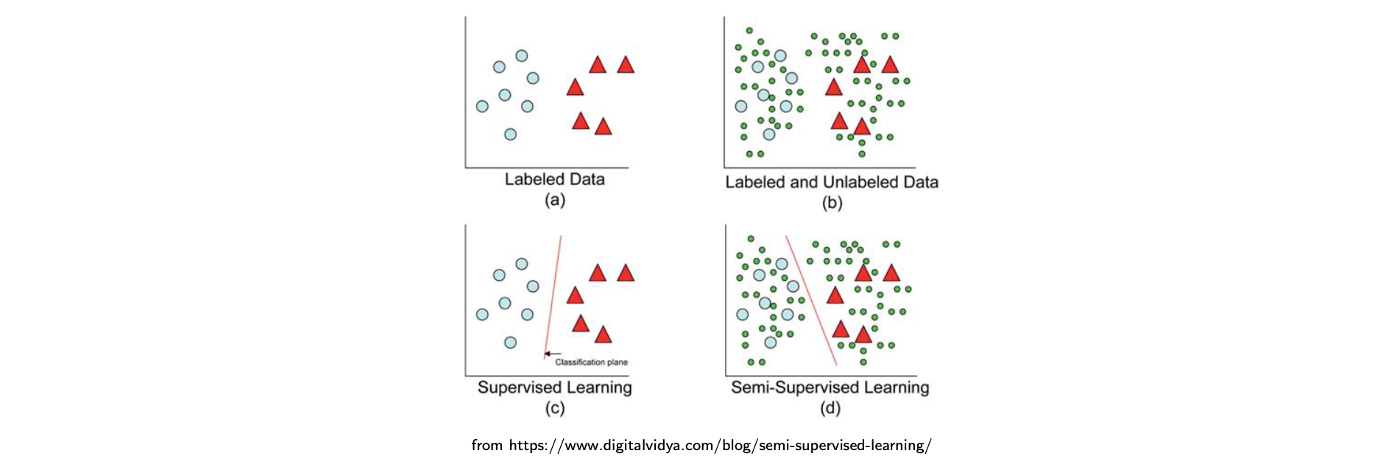많은 data를 가지고 있지만 일부만 label이 존재한다고 해보자. Labeled data만을 가지고 supervised learning을 진행하면 classification plane을 (c)와 같이 만들 수 있다. 반면 모든 data를 이용해서 semi-supervised learning을 진행했을 때 2개의 cluster가 만들어지고 label이 없는 data도 label이 cluster에 따라 있다고 생각할 수 있다. 그래서 이러한 semi-supervised learning을 사용하면 classification result를 기존의 (c)에서 (d)로 바꿀 수 있게 된다. 그 결과 더 나은 정확도를 만들 수 있다. 그래서 auto-encoder는 이렇게 semi-supervised learning에 사용이 되고 다음은 auto-encoder를 실제로 어떻게 semi-supervised learning에 사용하는지이다.

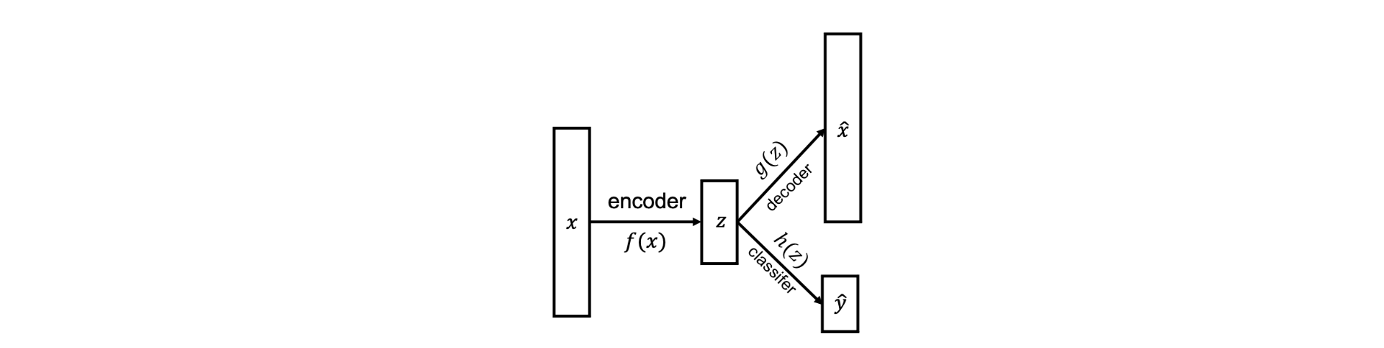
1. 먼저 labeled data와 unlabeled data를 포함하여 전체 dataset을 autoencoder로 학습시킨다. 그러면 data point를 잘 설명하는 feature가 만들어지게 된다.
2. 우리가 원하는 것은 classifier를 만드는 것이기에 encoder를 feature exctractor $f$로 사용하고 몇개의 layer를 사용해서 classifier $h$를 만들 수 있다. 그러면 classifier $h:R^M\rightarrow[0,1]$은 $f$로부터 추출 된 feature를 사용할 것이다.
3. 마지막으로 labeled dataset을 사용해서 $h$를 fine-tuning하면 된다.

이렇게 하면 encoder의 경우 모든 data를 사용해서 완전히 이해시키는 과정이고 classifer는 labeled data를 이용해서 학습하게 된다. 우리는 encoder에서 parameter의 수를 줄일 수 있어서 classifier에서는 적은 수의 parameter만을 사용할 수 있게 된다. 그렇기 때문에 적은 수의 parameter는 쉽게 학습될 수 있는 것이다. 이러한 과정을 통해서 semi-supervised learning을 진행하게 되고 전체 dataset을 이용해서 data의 전반적인 이해를 시키고 이를 기반으로 classifer를 학습시키게 된다.

Dimensionality Reduction for Visualization

Machine learning task를 위해서 unspervised learning 혹은 dimensionality reduction을 하게 되고 이러한 과정은 model을 설명하는데 굉장히 도움이 된다. 더불어 dimensionality reduction은 non-trivial space를 2차원에서 visualization을 할 수 있도록 한다. 그러면 사람이 data를 쉽게 이해할 수 있게된다. 물론 PCA나 KPCA를 사용해서 visualization을 할 수 있다. 그러나 PCA 결과는 한계점이 존재해서 그리 좋지 못한 방법이다. 그래서 사람들이 data point 사이의 similarity나 distance를 보여주는 다른 방법을 고안해냈다. 바로 t-SNE로 t-Stochastic Neighbor Embedding이다.

Example of t-SNE

t-SNE는 확률적으로 data point 사이의 similarity를 보존하려고 노력하고 다음과 같이 시각적으로 괜찮은 결과를 보여준다.
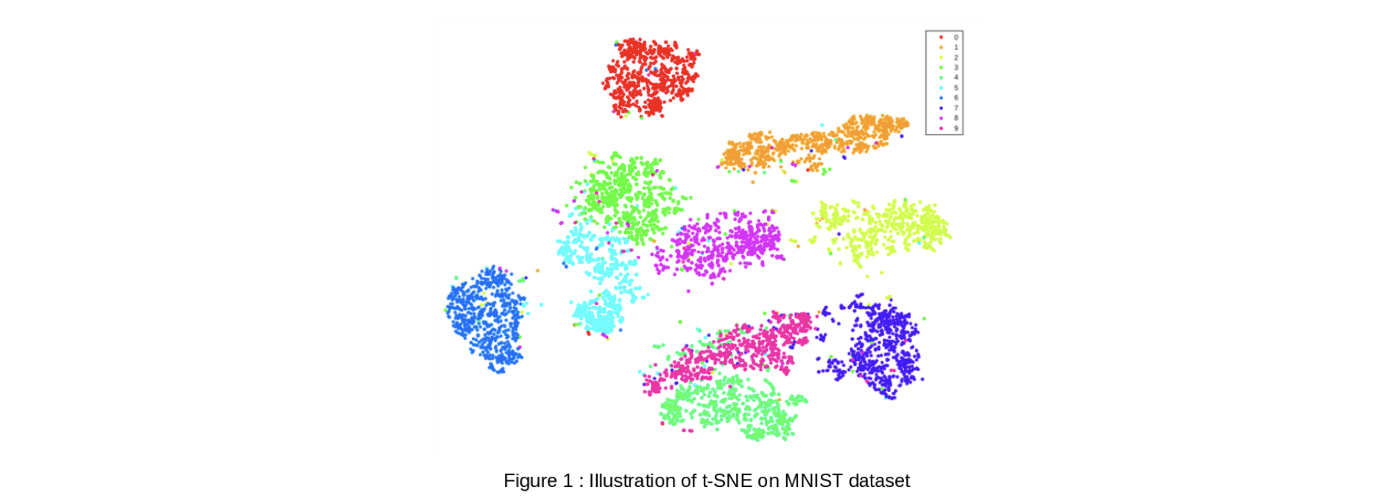t-SNE는 비슷한 data를 cluster로 만들어서 쉽게 분석할 수 있게 해준다. 위의 결과는 MNIST dataset의 t-SNE 결과를 보여주는 예시이다. 각 point는 dataset에 포함된 data를 나타내고 색은 대응되는 label을 보여주게 된다. 이렇게 visualization 하기 위해서 MNIST dataset을 model을 통해서 학습시키고 latent variable을 0~9까지 예측하도록 한다.