[기계학습] Dimensionality Reduction(PCA) 2

PCA를 eigenvalue decomposition으로 이해할 수 있고, 2가지 관점으로 의미를 해석할 수 있었다. 하나는 maximum variance이고 다른 하나는 minimum error이다. 그리고 정말로 높은 차원의 PCA를 수행하기 위해서 trick을 사용하여 계산적으로 수월하게 진행할 수 있었다. 지금부터는 factor analysis라는 주제로 더 일반적인 dimensionality reduction에 대해서 알아보고자 한다.

Factor Analysis

Factor anaylsis는 probabilistic model을 기반으로 진행된다. 그래서 data의 실용적인 특징들을 더 쉽게 얻을 수 있을 것이다. PCA는 eigenvalue decomposition으로 이해 되면서, minimum error와 maximum variance의 관점으로 PCA는 data를 압축하는 방법이 된다. 그러나 여기에는 non-linearity가 존재하고 data에 대한 어떠한 사전 지식도 존재하지 않는다. 단지 PCA에 의해 유도된 transformation을 통해서 data 손실을 최소로 만들려고 시도하는 것뿐이다. 그러나 이러한 관점은 다음과 같은 data distribution이 존재할 때에는 limitation으로 작용한다.
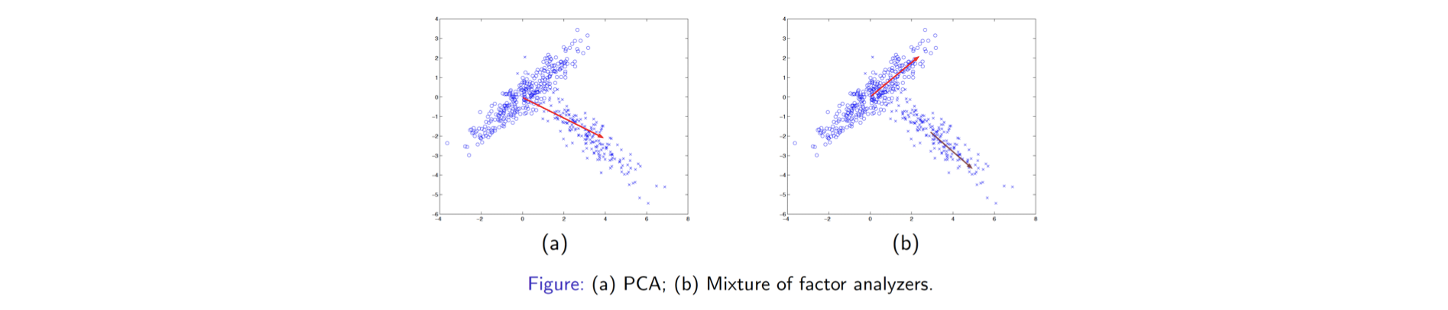2개의 component가 위와 같은 분포로 존재하며 하나는 우상향하고 다른 하나는 우하향하고 있다고 가정해보자. 이러한 data가 주어졌을 때 PCA는 오로지 어떻게든 data를 줄이려는데 초점을 둘 것이다. 사람이라면 보자마자 2개의 다른 component가 있다면 각 cluster에 대해 총 2개의 다른 PCA를 해야한다고 생각한다. 그러나 일반적인 PCA는 이렇게 할 수가 없다. 일반적인 경우 2차원의 data를 1차원으로 줄이게 되면 위와 같이 단순한 빨간 벡터로 끝날지도 모른다. 어찌보면 의도와 달라서 만족스럽지 못한 결과가 될 것이다.

그래서 data component가 여러개가 합쳐진 형태라고 판단이 되었을 때 factor analysis(FA) 혹은 probabilistic PCA(PPCA)는 generative model을 채택하게 된다. 즉, 위에서 (b)와 같이 각각의 결과로 판단하겠다는 이야기다. 이러한 방식은 더 정교한 dimensionality reduction 결과로 이어지게 되며, 이렇게 하는 것이 더 일반적인 접근법이 되어 data 손실을 줄일 수 있게 된다. 이러한 부분이 FA 혹은 PPCA의 동기가 된다.

Generative Model in Factor Analysis

FA를 이해하기 위해서 linear generative model을 이용하고자 한다. 이 model은 $D$ 차원의 data $x$를 만들고 이 data는 $M$ 차원의 latent factor $y$에 대응될 것이다. 일반적으로 투영 시키는 차원 $M$이 기존의 data의 차원 $D$ 보다 많이 작다고 가정하면 되고, 이를 기반으로 linear generative model을 다음의 식으로 설명할 수 있다.

Observation $x$는 latent factor $y$로부터 만들어지며, matrix $A$는 $M$차원을 $D$차원의 공간으로 바꿔주는 일종의 transformation이고 추가적으로 bias $\mu$와 noise $\varepsilon$이 더해지게 된다. $A$는 $D\times M$ matrix로 factor loading matrix라고 알려져있다. $y$는 $M$차원의 Gaussian latent variable로 가정해야 한다. 즉, $p(y_n)=\mathcal{N}(y_n|0,I)$으로 0 mean과 identity covariance를 가지는 Gaussian distribution이다. $\varepsilon$도 $D$차원의 Gaussian noise로, $p(\varepsilon_n)=\mathcal{N}(\varepsilon_n|0,\Sigma)$을 따르게 된다. 여기서 covariance matrix $\Sigma$는 $D \times D$ diagonal matrix가 된다. 그리고 $\mu$는 bias term으로 non-zero mean을 따르는 parameter vector이다. 그래서 요약하자면 observed distribution $x$는 다음과 같다.

MLE의 식으로부터 $\mu, A, \Sigma$를 찾는 것이 FA의 목적이다. 이를 진행하고나면 결과적으로 $y$를 쉽게 찾을 수 있고, 이는 곧 dimensionality reduction을 수행하게 되는 셈이다. $x$를 나타내기 위해서 $D$개의 많은 parameter가 필요하고, data가 $N$개 있다고 하면 총 ( $D\times N$ )개의 parameter가 필요하게 된다. 그러나 이러한 probabilistic model 혹은 generative model을 사용하고 $\mu, A, \Sigma, y$를 찾게 되면 ( $M\times N + \mu, A, \varepsilon$ ) 개로 줄어들게 된다. 그래서 우리는 $\mu, A, \Sigma$를 찾는데 앞으로 초점을 두고자 한다.

매우 간단한 regression task라서 쉽게 MLE 식을 만들 수 있을 것이다. 그래서 우리는 latent $y$의 값이 주어질 때 $x$의 값을 예측하고 싶다. 그리고 여기서 이러한 것을 underdetermined problem이라 하고 싶다. 왜냐하면 factor loading matrix $A$가 unique하지 않기 때문이다. 특히 rotation 연산을 제공해주는 orthogonal marix $R$을 추가해서 $A'=AR$로 rotated factor loading matrix로 정의한다면 다음과 같이 기존의 generative model이 바뀌게 된다.

$y'$은 $R^Ty$로 rotated latent variable이 된다. $R$을 orthogonal matrix로 가정했기 때문에 $R^T$와 곱하게되면 identity matrix가 되어 결국 기존의 식과 동일한 것을 볼 수 있다. 그리고 우리는 결코 true $y$를 볼 수가 없게 되어서 이는 underdetermined problem이 된다. 여기서 rotation은 그리 중요하지 않아서 크게 신경쓰지 않을 것이다.

Remark on Factor Analysis

위의 linear generative model에서 MLE의 solution을 찾는 방법으로 EM algorithm을 생각해볼 수 있다. 왜냐하면 오직 $x$를 본다고 했을 때 latent variable $y$가 존재하기 때문이다. 동시에 우리는 parameter $\mu, A, \varepsilon$을 예측할 수 있다. 이러한 방식은 k-means algorithm과 굉장히 유사하다. Clustering algorithm에서도 $\pi_k, \mu_k, \sigma_k$ 등 model parameter를 찾으면서 동시에 $r_{ik }$도 찾아야 했다. 그러나 clustering에서 $r_{ik}$는 hidden 값이었다. 그래서 이러한 목적과 매우 유사한 것이 지금의 factor analysis이다. 그래서 MLE의 해를 찾기 위해서 factor anaylsis는 EM algorithm을 사용할 것이고, 이는 latent를 전혀 볼 수 없기에 likelihood를 approximation시킬 수 있으며 approximated likelihood를 model parameter에 관해서 최대로 할 수 있다.

그리고 $\varepsilon$이 일반적인 covariance matrix를 가지는 정규 분포를 따른다고 했는데, 여기서 이 matrix를 isotropic matrix로 대체하게 되면 Tipping과 Bishop에 의해서 제안된 PPCA를 줄일 수 있게 된다. 어지됐든 FA는 일반적인 dimensionality reduction이고 unsupervised learning의 MLE estimation이다. 물론 Gaussian distribution 외에도 다른 distribtuion을 사용해도 좋다. 다만 설명의 편리함과 간단함을 위해서 Gaussain을 예로 든 것이다. 다음은 EM algorithm의 미분 과정을 디테일하게 설명한 것이다.

MLE of µ

EM algorithm을 사용하기 위해서는 먼저 log-likelihood를 정의하고 가야한다. Marginal distribution을 직접 계산하는 것은 어렵지만 가능하다. 하지만 이러한 접근 보다는 어떻게 문제를 수식으로 정의하고 이끌어낼 수 있는지가 더 중요한 부분이다. 그래서 EM algorithm을 유도하기 위해서는 complete-data log-likelhood를 위와 같이 정의해야 한다.

$\mu$를 data의 평균으로 정의했는데 $x=Ay+\mu+\varepsilon$에서 $y, \varepsilon$이 0 mean이기 때문에 $Ay, \varepsilon$은 bias가 존재하지 않게된다. 그래서 직관적으로 $\mu$는 likelihood를 최대로 하는 평균이 되어야 한다. 그래서 $\mu$를 이상적으로 선택하게 되면 average vector가 된다. 이제 편의성을 위해서 $x$를 0 mean으로 가정할 것이고 FA를 위한 EM algorithm을 진행할 것이다.

EM Algorithm for Maximum Likelihood Factor Analysis

E-step은 complete-data log-likelihood의 expected function을 계산하는 단계이다. 여기서 $y$는 latent variable이고 알지 못하는 값이다. 그래서 expectation이 $y$에 관해서 구해지게 되고 이때 observed data $X$와 model parameter $A,\Sigma$가 주어질 것이다. M-step은 complete-data log-likelihood로부터 계산이 된 function으로부터 model parameter인 $A,\Sigma$를 최대로하는 것을 목표로 하게 된다.

Gaussian Identities Lemma

EM algorithm을 수행하기 위해서는 Gaussian identities lemma를 다시 볼 필요가 있다.

E-step for ML-FA

M-step for ML-FA

EM for ML-FA

Mixture Factor Analysis

Mixture FA는 mixture distribution을 가정으로 한다. 2개의 mixture of Gaussian이 있고 우리는 자세한 parameter들에 대해서 알지 못하지만, 대략적으로 2개의 component가 있다고 생각할 수가 있다. Mixture FA의 derivation은 굉장히 복잡하지만 과정상 똑같이 진행이 가능하다.

지금까지 dimensionality reduction 기법들에 대해서 알아보았는데 특히 PCA와 FA에 대해서 알아보았다. 이러한 기법들은 curse of dimensionality를 극복하는데 유용하게 사용이 된다. PCA와 FA를 사용하면 dataset의 크기를 압축할 수 있고 data를 visualization 할 수 있어서 고차원의 data를 이해하는데 도움을 줄 수 있다. 그리고 PCA에서 linear data compression에 대해서 살펴봤는데 여기서 linearity가 표현하는데 있어서 종종 제한적이다. 즉, linearity가 dimensional reduction이 data의 손실을 크게하는데 피할 수 없게 만든다. 그래서 작은 차원으로 더 많은 정보를 표현하기 위해서 non-linear data compression을 생각할 수 있고 kernel PCA가 한 예시가 된다.