[기계학습] Generative Model - Variational Auto-Encoder(VAE)

Generative Models

Generative model의 목적은 training data distribution $P_{data}(x)$와 관련있다. Training data가 주어졌을 때, 동일한 distribution으로부터 새로운 sample을 만들고자 한다. 즉, data의 density를 예측하고 modeling하기를 원한다. 왜 generative model은 새로운 data를 만들어내는 function을 만드는 것이 아닌 data의 density를 예측하고 modeling 한다고 하는 것일까?

Application of Generative Model

Generative model은 여러 machine learning task에 유용하게 사용이 된다. Generative model에 대해서 알게되면 image-to-image translation 같은 분야도 할 수가 있다. Image-to-image translation에는 여러 분야들이 포함되어 있으며, 대표적으로 super-resolution, style change, colorization 등이 있다. 이러한 것들이 중요한 이유는 우리가 항상 충분한 자원을 가지고 있지 않기 때문이다. 이외에도 정말 다양한 분야에 적용이 가능한 것이 바로 generative model이다.

전혀 관련이 없어 보이는 POSCO steel과 같은 기관도 generative model을 사용하기도 한다. 이들이 만들어내는 제품 중에 random pattern을 가지는 plate가 있다. 이전에는 디자이너를 고용해 직접 pattern을 디자인했지만, 너무 크고 반복되는 작업량에 비효율적이었다. 그래서 대리석과 같은 pattern을 generative model에 학습시켜서 무한히 반복되는 pattern을 만들어내도록 했다.

Ordinary Auto-encoder(AE) for Data Generation?

Generative model에서 중요한 부분은 training data의 density를 학습한다는 점이다. 그래서 generative model과 가장 관련이 있는 것이 바로 auto-encoder(AE)이다. 우리는 data를 만든다고 했을 때 AE를 생각해볼 수 있다. 그러나 비록 input data에 대해서 괜찮은 설명을 잘 요약하고 압축한다고 할지라도 AE를 data generation에 적용하는데에는 어려움이 있다. AE를 사용하게 되면 새로운 data들이 만들어지지 않고 latent feature에 대한 구체적인 이해도 없는 상태가 된다. 이는 압축하기 좋다는 것을 의미하지만 가능성 있는 latent code의 distribution에 대한 이해가 전혀 없게 되는 단점이 존재하게 되는 것이다.

반면, VAE는 latent code에 대한 regularization을 제공해준다. 그래서 새로운 image를 만들 수 있게 되고, 주어진 image에 대해서 흥미로운 수정본도 만들어낼 수 있다. 그래서 AE를 data generation에 사용하지 않는 이유는 AE를 학습시키기 위해서 여러 data가 있다고 했을 때 AE는 동일한 image를 요약하고 재구성하는 작업은 잘하지만 우리가 generative model에 진정으로 원하는 것은 새로운 image를 만드는 것이다. 그래서 새로운 image를 만들기 위해서 새로운 latent code를 사용하는 것을 생각할 수 있지만, latent code에 무엇이 가능성이 있고 그럴듯한지는 알지 못한다. 그래서 AE는 data generation에 적용하기는 다소 어려움이 존재하는 반면 VAE는 latent code의 structure에 probabilistic approach를 제공해주고 새로운 image를 만들어내고 통제할 수 있게 된다.

Manipulating Latent Feature

Latent space에 대해서 이해할 수 있게 되면 다음과 같이 가능해진다.
통제가 가능한 latent feature가 있다고 해보자. 우리는 필요한 정보를 기반으로 image를 만들어낼 수 있다. 위와 같이 안경을 쓴 남자에 대해서 학습을 시키고 안경을 쓰지 않은 남자에 대해서 학습을 시키고 또한 안경을 쓰지 않은 여자에 대해서 학습 시킬 수 있다. 이러한 3가지의 정보를 이해하는 것으로부터 안경을 쓴 여자를 만들어내는 것을 생각해볼 수 있다. 이를 위해서 안경 쓴 남자, 안경을 쓰지 않은 남자, 안경을 쓰지 않은 여자에 대한 latent vector를 만들었다. 그리고 평균치를 내어 위와 같은 연산을 통해서 안경을 쓴 남자에서 남자가 사라지고 안경이 남고 여기에 여자 얼굴을 합쳤다고 볼 수 있다. 시간이 지나면서 많은 연구들이 latent feature들을 조작하는데 효과적인 방안들을 제시해왔다. 이러한 간단한 연산 외에도 style transfer 분야 등에도 적용할 수 있다.

위의 사진들은 CyclerGAN이라는 연구의 결과로 image-to-image translation의 한 예시이다. 여기서는 갈색 말이 주어졌을 때 얼룩말을 만들어내고, 사과가 주어졌을 때 오렌지를 만들어내고자 했다. 이렇게 style을 바꾸는데에 latent feature를 기반으로 사용한 것이다.

General Apporach: Maximum Likelihood

Generative model을 만들기 위해서 확률이 높은 latent space를 build하는 것이 매우 중요하며, 이는 어떠한 조건 아래 새로운 image나 data를 만들어낼 수가 있다. 이를 위해서 가장 일반적인 방법으로 간단한 maximum likelihood를 notion으로 사용하면 된다.
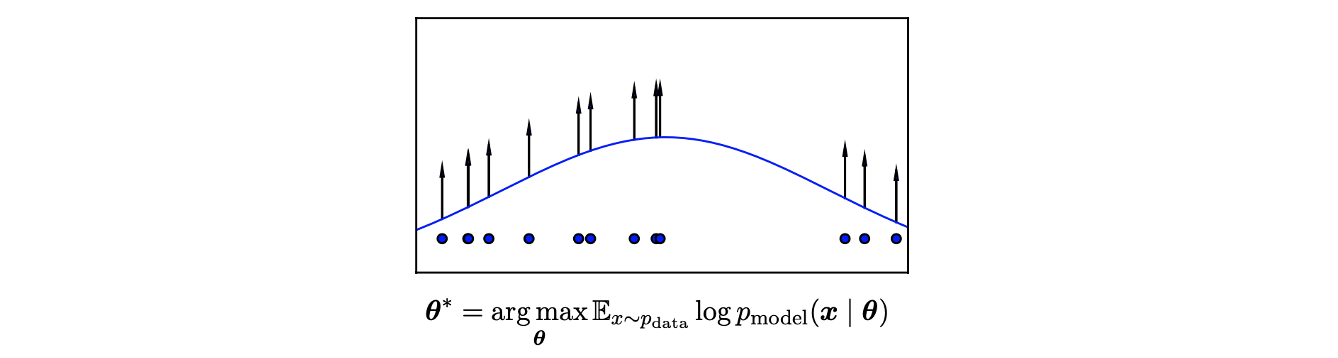우리가 원하는 것은 model parameter를 최적화하면서 likelihood에 대한 model을 찾는 것이다. 이러한 부분이 generative model에서 실제로 원하는 부분이다.

Taxonomy of Generative Models

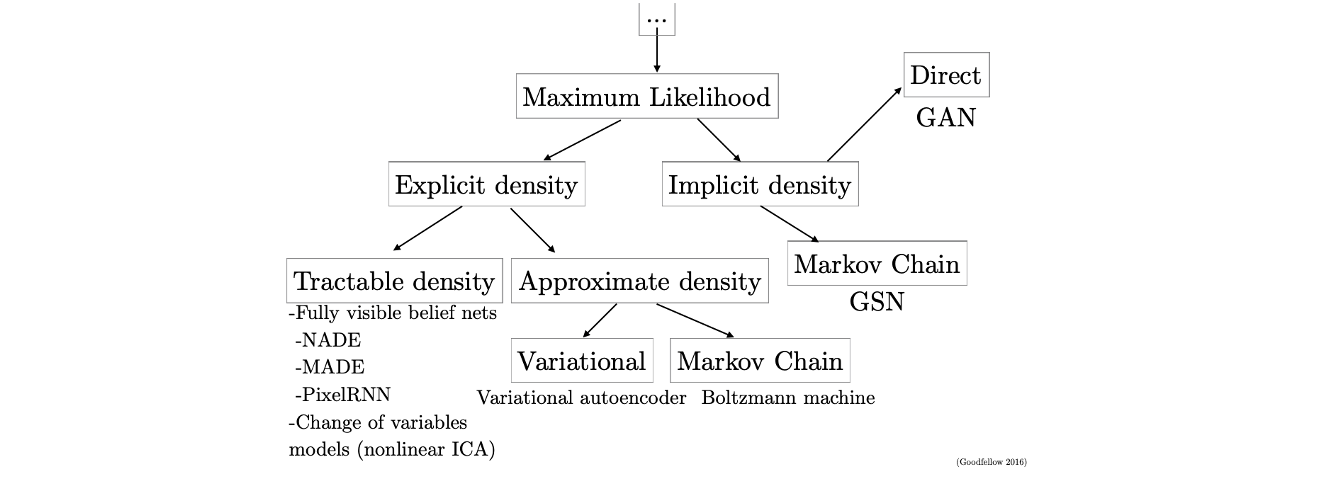
Variational Auto-Encoder(VAE)

Manifold Hypothesis

VAE를 이야기하기 앞서 VAE를 디자인하기 위한 가설에 대해서 이야기하고자 한다. 이 가설은 manifold hypothesis로 data point $x$가 고차원의 vector일 때 이 data 들이 낮은 차원의 manifold 주변에 집중되어 있다는 것이다.
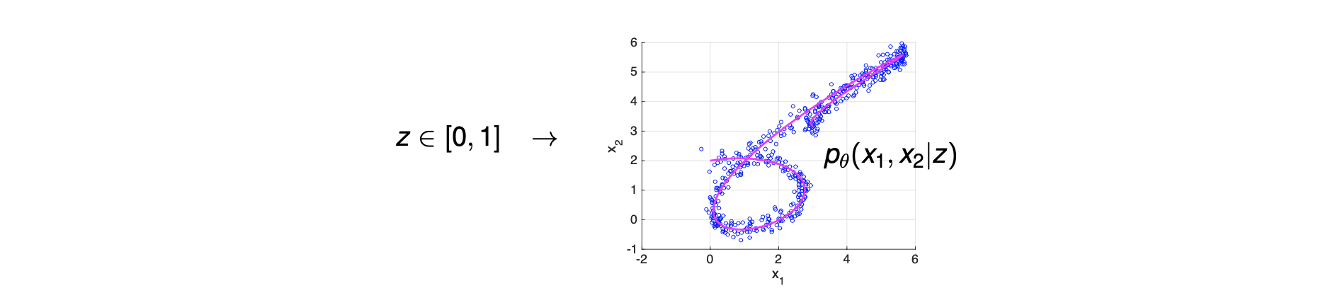예를 들어 위와 같이 2차원에 data가 분포하고 있다고 해보자. 우리가 가정하는 것은 쉽게 만들 수 있는 manifold 혹은 function이 있고 실제 data가 이 function 주변에 분포하고 있다는 것이다. 위의 예시에서 파란 점들은 real data이고 빨간 선은 manifold이며, 대부분의 generative model은 이러한 manifold hypothesis를 기반으로 만들어진다. 다음은 image data를 이용해서 manifold hypothesis를 설명한 것이다.
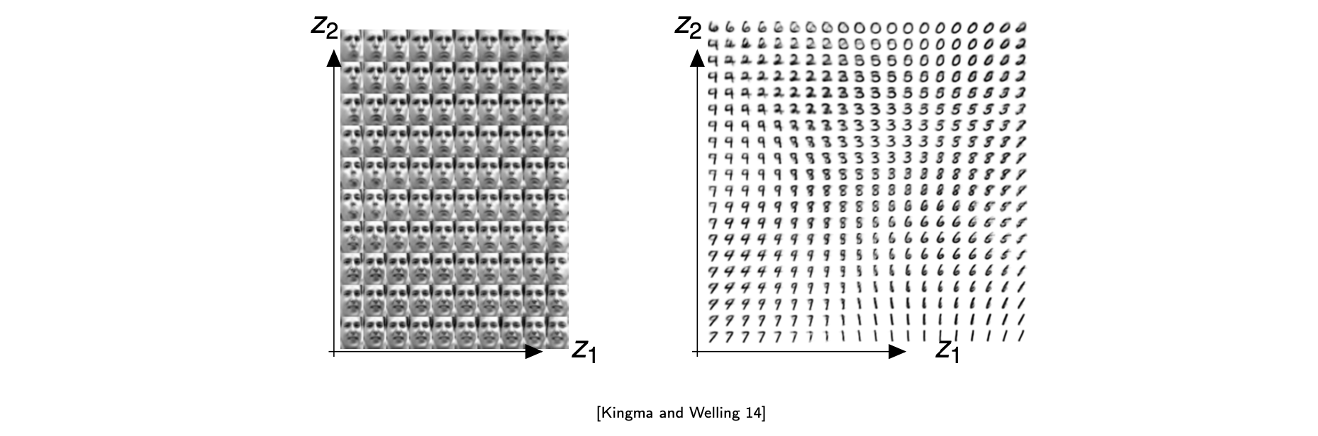모든 image는 고차원의 vector일 것이며 manifold hypothesis로부터 우리는 차원을 낮출 수가 있다. 즉, real data point의 distribution을 이전의 고차원에서 저차원에 나타낼 수가 있다. 특히, 평균적으로 가장 전형적인 image나 data가 중심에 놓인다는 가정도 함께 생각할 수 있다. 위의 예시에서는 정면을 바라보는 얼굴이 중앙부에 놓여있으며 외곽으로 갈수록 구체적인 특징이 존재하는 얼굴들이 분포하게 된다.

Probabilistic Approach for Generative Model

Manifold hypothesis를 기반으로 generative model을 위한 probabilistic approach를 만들 수 있다.

$p_\theta(x|z)$는 generative model이고 $p(z)$는 prior이다. 우리의 목적은 $p_\theta(x)$를 최대로 만드는 것이다. 여기서 prior는 간단하게 선택할 수 있으며 일반적으로는 Gaussian distribution을 선택하곤 한다. 그리고 latent code로부터 data point generation은 다소 복잡해서 neural network를 사용하게 된다. 이러한 것들이 generative model 중에서도 VAE를 시작하기 위해서 알아야하는 내용들이며, manifold hypothesis에 대해서 가장 일반적으로 접근하는 방법이다.

비록 latent vector의 prior distribution $p(z)$를 고정한다고 하더라도 conditional probability $p_\theta(x|z)$가 neural network이기에 marginalization $\int$를 계산하는 과정은 매우 어렵다. 이러한 계산적인 어려움이 대부분의 machine learning task에 나타나기에 EM algorithm, BP algorithm 등을 알아둬야 한다. 그래서 이렇게 다루기 어려운 marginalization에 대해서 우리는 variational inference method를 적용할 예정이다. 그래서 likelihood를 알아내기 위해서 marginalization의 계산적인 어려움을 피해가도록 할 것이다.

Generative model을 만드는 것은 likelihood $p_\theta(x)$를 예측하는 것과 같다. 그러나 manifold hypthesis를 고려하면 저차원에서 각 data마다 latent code가 존재해야한다는 것인데, 이를 기반으로 latent code의 존재를 생각하면서 likelihood를 새롭게 적은 식이 위의 식이다. 여기에는 latent code의 distribution이 존재하면서 원점 혹은 다른 manifold에 집중되어 있을 것이다. 만약 latent code가 주어지게 되면, 우리는 noise 등을 추가할 수 있고, 결국에는 새로운 data를 만들어낼 수 있게 된다. 이러한 insight를 담은 식이 위에서 새롭게 적은 likelihood의 식이다. Manifold hypothesis를 실현한 것이 prior $p(z)$와 일종의 decoder $p_\theta(x|z)$를 사용해서 likelihood로 나타낸 것이다.

Intractability

Computational intractabiltiy를 생각하면서 다음의 식을 여러 방법으로 분해해보고자 한다.

먼저, marginalization에서 $\int$는 다루기 어렵고 $z$가 범위가 큰 support로부터 존재한다고 했을 때 우리는 바로 $\int$를 계산할 수 없게 된다. 그리고 likelihood 또한 $\int$ 때문에 다루기 어려워서 posterior density를 통해서 피해가려고 시도했다.

Posterior를 적게되면 다시 한번 $p_\theta(x)$를 사용할 수 있게 된다. 우리가 분모에 대해서는 원래 알지 못했기에 posterior 또한 다루기가 어렵다. 그래서 이를 해결해보고자 posterior를 근사하는 방법을 사용했다. 이렇게 하면 likelihood를 계산할 수 있게 되고 최대로 만들 수가 있다. Posterior $p_\theta(z|x)$를 근사하기 위해서 또 다른 network로 encoder network $q_\phi(z|x)$를 사용할 수 있다.

Probabilistic Framework of Auto-Encoder

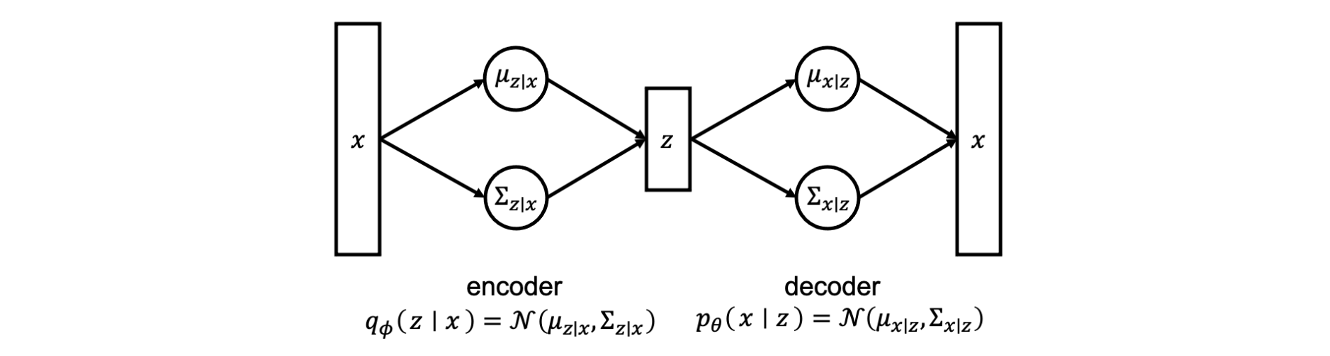Encoder network는 $x$를 input으로 받아서 random variable $z$를 만들려고 시도한다. 구체적으로 예를 들어서 $x$가 주어졌을 때 neural network가 $z$의 mean과 covariance를 찾는다고 해보자. 이렇게 얻은 정보들로부터 $z$를 sample로서 만들 수가 있다. 이 과정을 posterior distribution으로 볼 수 있고 $z$를 얻은 후에 decoder network를 이용해서 real image를 만들어낼 수 있다. 여기서 또 다른 neural network가 $z$가 주어졌을 때 $x$의 mean과 covariance를 찾을 수 있고, 이 정보를 이용해서 최종적인 random image를 만들어내는 것이다.

Encoder로부터 neural network $f_\phi$가 있다고 가정하게 되면 우리는 다음과 같이 정의할 수 있게 된다.

이와 비슷하게 decoder로부터 neural network $g_\theta$가 있다고 가정하게 되면 다시 유사하게 정의할 수 있게 된다.

$g_\theta$의 output은 $\mu,\Sigma$와 같은 density의 parameter들이고, $z$로부터 임의의 $x$를 만들 수 있다. 이러한 randomness가 VAE의 중요한 특징이다. 왜냐하면 지금까지 일반적인 AE는 randomness와 noise가 없고 단지 주어진 image를 재구성하는 것이 전부였다. 그래서 새로운 image를 볼 기회가 없었지만 VAE에서는 randomness가 존재해서 위와 같은 구조로부터 새로운 sample을 자연스럽게 만들어낼 수 있다.

Variational Autoencoder

그래서 주어진 model로부터 data likelihood를 최대로 하는 것이 우리가 해야하는 일이었고, 여기서 model은 $\theta$라는 parameter를 가지고 있다.
Likelihood $p_\theta(x)$를 최대로 하기 위해서 log-likelihood를 expectation으로 나타낼 수 있다. Encoder network로부터 latent variable $z$에 대한 expectation을 취한 것이고, $p_\theta(x)$는 $z$와 관련이 없어서 Bayes' theorem으로부터 $z$에 관한 식으로 변형할 수 있다. 그리고 자연스러워 보이지는 않지만 분자, 분모에 encoder network $q_\phi(z|x)$를 곱해준다. 이후 logarithm의 분해를 이용해서 식을 나눌 수가 있다. 마지막으로 KL divergence를 이용해서 식을 정리할 수 있다. 이렇게 만든 식은 $\phi,\theta$를 학습하기 위해서 우리가 최대로 만들고자 하는 objective function이 된다. 그렇다면 이제 이렇게 만든 식이 computionally tractable한지 아닌지를 봐야한다.
분명히 term (A)는 tractable하다. 우리는 $q_\phi$가 어떻게 생겼는지 알고 있다. 그래서 parameter $\phi$가 주어졌을 때 우리는 $z$를 sample로 얻을 수 있게 된다. 이로부터 monte carlo sampling을 이용하고 expectation을 근사한 뒤 derivative를 구할 수 있게 된다.

그리고 term (B) 또한 tractable하다. 우리는 prior와 posterior를 Gaussian distribution이라 가정했고, 2개의 Gaussian distribution으로부터 KL divergence를 나타내기 위해서 closed-form formula가 있다는 것을 알고 있다. 결국 term (B)도 위와같이 나타낼 수 있다는 것을 의미한다.

마지막으로 term (C)는 확률적이라 아쉽게도 intractable하다. 그러나 우리가 알고 있는 사실은 Gibbs' inequality 때문에 적어도 이 값이 음수는 아니라는 것이다.

그래서 VAE는 앞의 2개의 항인 (A)+(B)를 최대로 만드는데 초점을 맞추게 된다. 이를 evidence lower bound(ELBO) 라고 하며 이는 EM algorithm에서 보았던 내용과 매우 유사하다. 구체적으로 만들기 위해서 term (A)+(B)를 variational lower bound $\mathcal{L}(x,\theta,\phi)$라고 정의할 것이다. 여기에 사용된 것은 모두 term (A), (B)의 parameter로서 사용되는 것들이다.

Training VAE

지금부터는 VAE를 어떻게 학습을 시킬지에 대한 방법을 알아볼 것이다. VAE를 학습하는 것은 ELBO를 최대로 만드는 것과 같다.

$\text{Training VAE: }$

위에서 $\text{log }p_\theta(x)$를 전개하는 식이 매우 복잡했고, 어떻게 $q_\phi(z|x)$를 곱할 생각을 할 수 있었을까? 결과적으로 ELBO를 얻는 것이 어떠한 의미를 가지게 되었으며, 다음과 같은 식을 통해서 이해할 수 있다.

$\text{Understanding ELBO: }$

첫번째 항인 $E_z[\text{log }p_\theta(x|z)]$는 $z$로부터 주어진 $x$를 재구성하는데 초점을 맞추고 있다. 두번째 항인 $KL(q_\phi(z|x)||p_\theta(z))$는 regularization term으로 이해할 수 있다. Manifold hypothesis로부터 $p(z)$를 어떠한 concentration이 형성 된 distribution으로 가정했으며, prior로서 $p(z)$는 0 mean Gaussian distribution으로 가정했다. 그래서 이런 의미에서 posterior가 prior가 되도록 초점을 맞추게 된다. 즉, 우리는 서로 다른 distribtuion $q_\phi, p_\theta$가 서로 가까워지기를 바란다.

Training VAE: Monte Carlo Method (First Term)

이러한 내용들을 기반으로 구체적인 training algorithm으로 Monte Carlo method에 대해서 알아보려고 한다.

모든 것이 expectation을 최대로 만드는데 초점을 맞추고 있지만, 불행히도 $z$가 무한한 support를 가지고 있어서 marginalization이 computationally intractable하다. $\int$를 정확하게 계산하기 보다는 Monte Carlo method를 사용해서 expectation을 근사시킬 수 있다. 이 과정에서 $q_\phi$로부터 $z$를 sampling 할 수 있고, 여기에 평균을 취할 것이다. 이렇게 expectation을 근사를 시키고나면 back-propagation algorithm을 적용할 것이다.

Training Decoder $p_\theta$

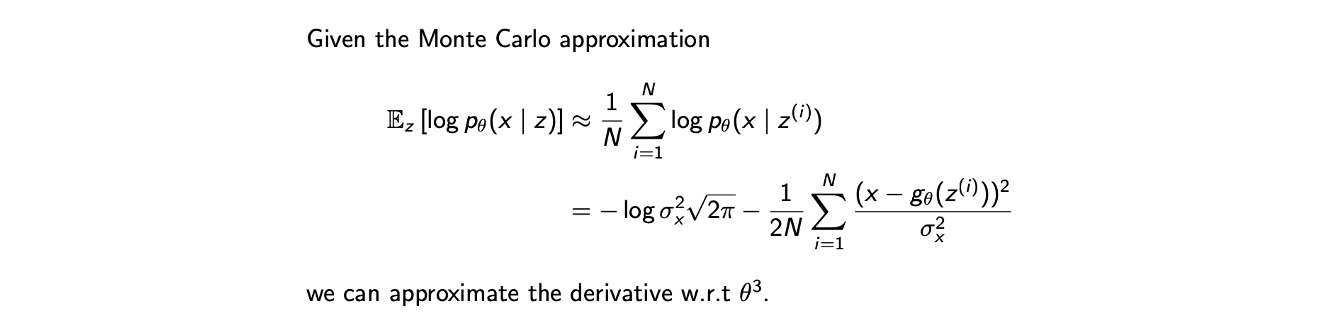Decoder $p$를 학습시키는 단계에서는 ELBO의 첫번째 항에서 Monte Carlo approximation을 하고 이를 Gaussian distribution parameter를 사용해서 식을 정리하게 되면, 이로부터 back-propagation algorithm을 수행해서 최종적으로 $\theta$에 대한 derivative를 구할 수 있다.
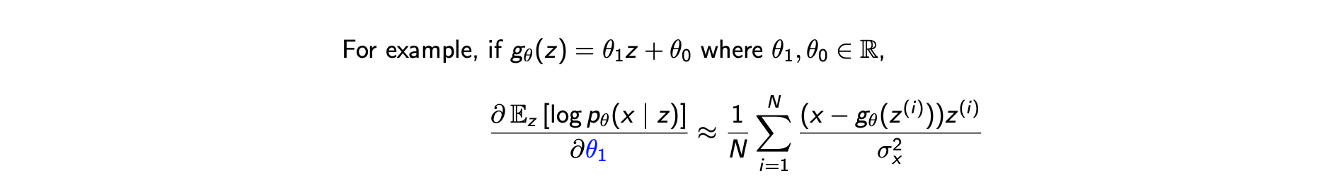그리고 예를 들어 $g_\theta(z)$가 위와 같을 때 첫번째 $\theta$에 대해서 위와 같은 결과를 얻게 된다.

Training Encoder $q_\phi$

그러나 encoder의 경우 non-trivial해서 비록 $z$를 $q_\phi$로부터 sampling 하더라도, 이 sampling 과정은 back-propagation을 매우 어렵게 만든다. $q_\phi$를 training하기 위해서 필요한 것은 $\phi$에 대해서 derivative를 취하는 것이다. 그러나 명시적인 표현이 없다. 사실 이러한 문제는 $z$가 오로지 $q$로부터 sampling 되기 때문에 생기게 된다. 우리는 sampling distribution을 이용해서 derivative를 취하기를 원한다. $q_\phi$에 대해서 derivative를 취하기 위해서는 reparameterization이라는 VAE를 학습시키는 일종의 trick를 사용해야 한다.

Reparameterization Trick

예를 들어 $Z$를 평균이 $\mu$이고 표준편차가 $\sigma^2$인 Gaussian random variable이라고 가정해보자. 그러면 $Z$의 ditribtuion은 standard normal distribtuion에 의해서 다음과 같이 설명될 수 있다.

$\epsilon$은 $\mu$나 $\sigma$와는 전혀 관련이 없는 constant distribution이다. 이러한 trick을 reparameterization이라 부르며, 이로부터 constant가 되는 $Z$를 sampling하는 과정에서 $\phi$에 관해서 randomness를 가질 수 있게 된다. 이는 매우 중요한 observation이다. 왜냐하면 여기서 $q_\phi$로부터 $z^{(i)}=\sigma\epsilon^{(i)}+\mu$에서 공유하는 parameter $\sigma,\mu$가 생기고 유일한 차이로는 constant distribution으로부터 온 random noise $\epsilon$만 남게된다. 그래서 우리는 이에 대해서는 derivative를 취할 필요가 없고 이를 constant 취급할 수 있게 된다. 결국 우리가 필요한 것은 $\sigma, \mu$에 대한 derivative만 남게 되어, $\phi$에 대해서 모두 미분이 가능해지는 결과가 된다.

Training Encoder with Reparameterization

이 내용을 다음과 같이 요약해서 설명할 수 있다.
여기서 $z^{(i)}, \epsilon^{(i)}$는 $\phi$에 대해서 constant로 여길 수 있고, likelihood에 대입해서 식을 다시 적을 수 있다. 그러면 이로부터 $\phi$에 관한 partial derivative도 표현할 수 있게 된다.

KL Divergence (Second Term)

Gaussian distribtuion으로 가정하게 되면 KL divergence는 매우 간단해진다. 2개의 Gaussian distribution $q,p$에 대해서 $p(z)$를 0 mean Gaussian distribtuion으로 가정하면 위와 같이 식을 얻을 수 있다. 이 식은 2개의 distribution의 KL divergence를 말하고 있고 이 식으로부터 $\phi$에 대해서 derivative를 취하면 된다. 이렇게 VAE를 training 시키는 방법에 대해서 알아보았다.

Training VAE: Summary

VAE를 training하는 것은 ELBO를 식으로 적는 것부터 시작하며 likelihood에 대해서 위와 같이 식을 나타낼 수 있다. 그리고 expectation을 근사시키고 KL divergence를 계산할 수 있다. 여기서 expectation은 Monte Carlo method에 의해서 근사되고, decoder $\theta$에 대해서 derivative를 구하는데 있어서는 단지 주어지게 되지만 encoder $\phi$에 대해서 derivative를 구하기 위해서는 reparameterization trick을 sampling operation에서 $\phi$의 dependency를 얻을 수 있는 곳에 사용해야 한다. 그러면 $\phi$에 대해서 derivative를 구하는 것이 가능해진다. 여기까지가 VAE를 학습하는 방법이었다.

Pros and Cons of VAE

VAE는 GAN과 비교되는 장단점이 존재한다. Density의 explicit estimation으로서 여러 trick을 사용하더라도 어찌됐든 probability를 구할 수 있기 때문에 이를 principled approach라고 부를 수 있다. 또한 encoder 구조를 사용한다는 점에서 여러 task에 적용이 가능하다.

반면, marginalization의 근사이기에 어느정도 loss가 존재하게 된다. 특히, decoder 구조는 random noise를 포함하고 종종 blurry하고 퀄리티가 낮은 결과를 만들어내게 된다.