[기계학습] Dimensionality Reduction(PCA) 1

Example of Unsupervised Learning

이번에는 unsupervised learning의 2번째 application인 dimensionality reduction에 대해서 알아볼 것이다.

Curse of Dimensionality

본격적으로 들어가기 전에 dimensionality reduction의 동기에 대해서 알아보고 갈 것이다. 우리는 machine이 data set으로부터 pattern을 알아내기를 원한다. 그리고 대부분 컴퓨터는 많은 양의 연산이 가능하다고 알고있다. 그래서 data의 모든 정보를 컴퓨터에 넣고서는 pattern을 찾고자 한다.

그러나 여기에는 trade-off가 존재한다. Data set으로부터 충분한 정보를 얻는 것이 중요한 것은 사실이다. 만약 그렇지 않으면 어떠한 것도 예측할 수 없을 것이다. 그러나 data의 양이 너무 많아지게 되면 문제가 발생하게 된다. 그리고 현실 세계에서의 data는 대부분 고차원의 정보를 담고 있다. 예를 들어 computer vision에서 고해상도의 image를 다루거나 natural language process에서 엄청나게 많은 단어들을 다루게 된다. 이렇게 data가 고차원일수록 더 많은 data sample들이 필요하다. 다음과 같이 1차원의 data가 있다고 가정해보자. 위의 예시에서 1차원의 data를 이해하기 위해서 3개의 구역을 커버해야 할지도 모른다. 만약 10개의 sample이 있다면 적어도 3개의 sample을 이용해서 각 구역을 커버할 수 있다. 굉장히 그럴듯한 이야기같지만, 만약 차원을 늘린다면 9개의 구역을 커버할 필요가 있다. 10개의 sample이 있기 때문에 각 구역당 1개의 sample을 할당해서 커버하면 된다. 이 역시도 그럴듯해 보인다. 그러나 만약 차원을 다시 늘리게 되면 27개의 구역이 생겨서 10개의 sample로 모든 구역을 커버할 수 없다. 즉, 차원이 증가함에 따라 우리는 관찰하지 못한 일부 구역을 포괄하는 보다 정교한 알고리즘을 가져야 한다.

충분한 data point를 가지고 있다면 모든 것이 괜찮지만, 이 숫자는 차원의 측면에서 기하급수적으로 증가하게 된다. 이러한 내용이 바로 curse of dimensionality이다. 현실 세계에서 공부하는 경우도 이와 같다. 공부를 하면할수록 더 해야한다는 것은 몸소 느낄 것이고 이러한 것도 curse of dimensionality의 일종으로 볼 수 있다.

True vs. Observed Dimensionality

다음과 같이 $10\times 10$ bitmap image가 있다고 해보자.
각 image의 차원수는 100이고, 이 숫자는 너무 큰 값이다. 이론적으로 이 차원과 data set을 이해하기 위해서는 적어도 $2^{100}$개의 smaple이 필요하다. 그렇다고 이 모든 sample들이 충분한 정보를 가지고 있지 않을 것이고 일부는 정보가 부족할 수 있다. 만약 우리가 이 bitmap을 이용해서 손글씨를 표현한다면 대부분 위의 좌측의 예시와 같이 나타날 것이다. 그러나 위에서 두번째, 세번째 image와 같이 모두가 올바르게 손글씨처럼 보이지 않고 정보가 부족해서 굳이 학습할 필요가 없는 bitmap도 많을 것이다. 그래서 이러한 내용이 dimensionality reduction의 하나의 가능성을 제시해주게 된다. 차원수가 100이라면 그럴듯한 data를 포함하는 subset 또는 manifold가 있어야 하고, 이러한 부분에 중점을 둔 기법으로 pricipal component analysis(PCA)를 살펴볼 것이다.

Principal Component Analysis(PCA)

Introduction of PCA

직관적으로 dimensionality reduction 혹은 PCA 기법은 data를 더 낮은 차원으로 투영하는 것을 목표하고 있다. 다음과 같이 2차원의 data가 있다고 해보자.
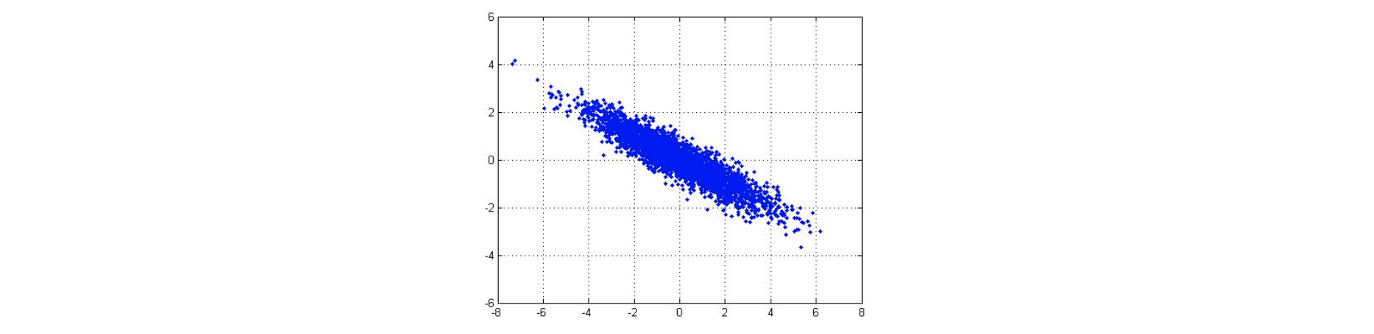우리는 이 data를 1차원으로 투영하고 싶다. 가장 단순한 방법은 하나의 선을 그리고 투영시켜서 차원을 축소시키는 것이다. 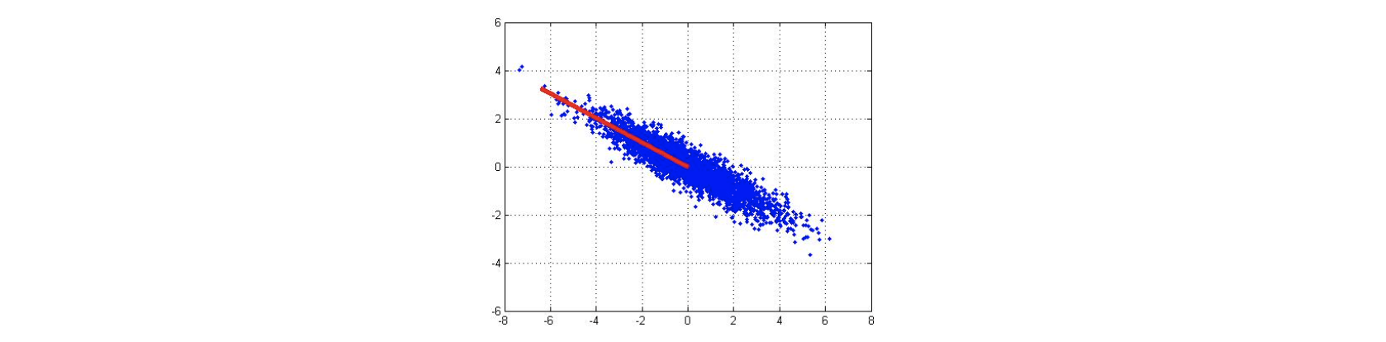위의 파란점들을 data $(x_i,y_i)$라고 하자. 여기서 point들을 표현하기 위해서 2개의 parameter가 필요하기 때문에 이 data set이 2차원에 있다고 할 수 있는 것이다. 그래서 이 data를 위의 빨간선 위에 투영시킨다고 했을 때 그 선 위의 data를 $(x'_i,y'_i)$라고 할 것이다. 그리고 이 선을 $y=ax+b$ 라고 해보자. 그러면 이제 projected point를 $y'_i=ax'_i+b$ 라고 나타낼 수 있다. 이제 projected point를 하나의 parameter로 표현이 가능해졌다. 이 data point는 이제 $(x'_i,ax'_i+b)$로 표현이 가능하다.

Linear algebra에서 이러한 선을 basis라고 부르고, 우리는 차원을 축소하기 위해서 새로운 basis를 찾기를 원한다. 100개의 sample을 2차원에 표현하기 위해서는 $(x_1,y_1)$부터 $(x_{100},y_{100})$까지 총 $2\times 100$ 개의 variable이 필요하다. 축소된 차원인 1차원에서는 $2+1\times 100$ 개의 variable이 필요하다. 여기서 2는 basis를 나타내기 위한 parameter $a,b$를 의미한다. 지금까지 내용으로 차원을 축소하기 위해서는 투영이라는 것이 동반된다는 것을 확인할 수 있었다. 투영을 위해서 아무런 basis나 사용할 수는 없는 것이다. Basis에도 good basis와 bad basis가 존재한다. 어느 것이 good basis인지 판단하기 위해서 다음 2개의 예시를 보도록 하자.
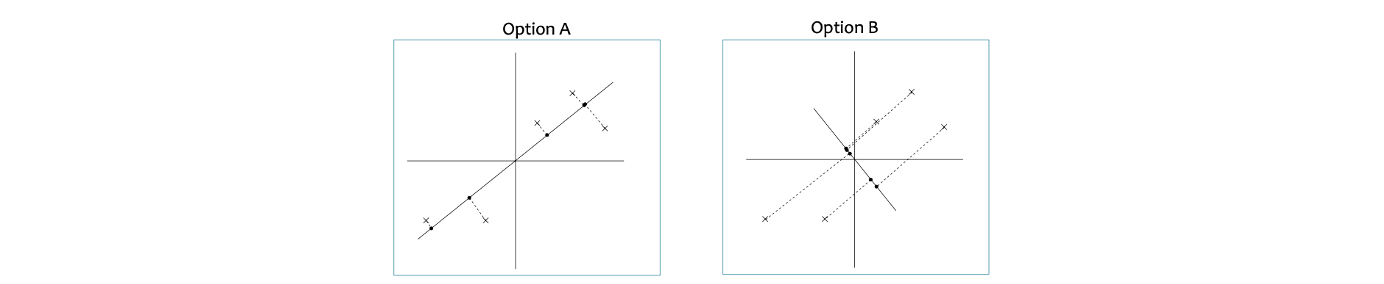2개의 예시는 서로 다른 basis와 서로 같은 data point들로 이루어져 있다. 이 예시들을 보고 어느 것이 더 나은 basis인지 단번에 말할 수 있는가? A의 경우 투영을 시켰을 때 투영시킨 지점까지의 거리가 대부분 짧기 때문에 정보의 손실이 적을 것이다. 반면, B의 경우 투영시키는 지점까지의 거리가 매우 길다. 그래서 B의 경우 정보의 손실이 A보다 많을 것이다.

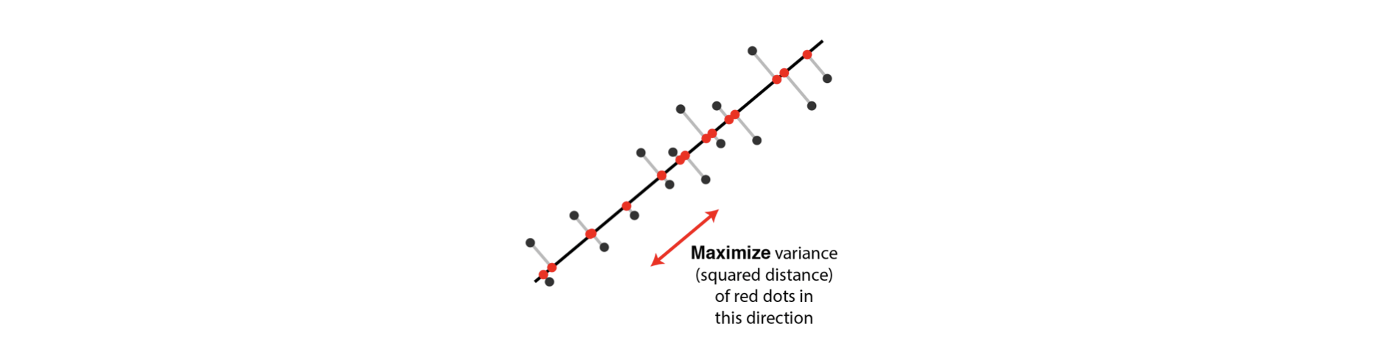
이외에도 또 다른 이유도 존재한다. A의 경우 projected point들이 직선 상에서 최대로 퍼져있다. 만약 모든 data를 0차원으로 차원 축소를 시킨다면 모든 point들이 하나의 point로 모이게 될 것이다. 이 말은 data들이 서로 구분되는 차이가 존재하지 않아서 정보의 손실이 발생하게 된다. 반대로 우리는 good basis는 line에 projected point들이 최대로 멀리 퍼져있다는 것으로 이해할 수 있다. 이러한 2가지 관점으로 PCA를 진행하고자 한다.

Maximum Variance Formulation

Maximum variance는 dimensionality reduction의 하나의 목표로 여겨진다. Variance를 최대로하는 것은 projected data set의 정보를 최대로 하는 것과 같다. 그래서 maximum variance formulation이란 것을 알아볼 것이다. $x_n \in R^D$인 dataset $\{x_n\}_{n\in[N]}$이 있다고 가정하자.

1-Dimensional Principal Subspace

우리의 목표는 data를 projected data의 variance를 최대로 하면서 $D$보다 작은 $M$차원의 공간으로 투영하는 것이다. 구체적으로 예시를 들기 위해서 $M=1$ 이라고 가정해보자. 그러면 1차원으로의 projection은 unit vector $u_1\in R^D$으로 설명할 수 있다. 여기서 unit vector라는 것은 각 norm이 1이라는 것이다($u_1^Tu_1=1$). 그리고 각 data point $x_n$은 $u_1^Tx_n\in R^1$으로 투영된다. 그러면 projected data의 variance는 다음과 같다.

여기서 $\bar{x}$는 average를 의미하고, $u_1^T\bar{x}$ 는 projected point들의 average를 의미한다. 그래서 variance는 data point의 average point를 투영한 것과 data point들을 투영한 것 사이의 squared distance로 계산될 수 있다. 그리고 이를 data point의 개수인 $N$으로 나눠주게 되면 covariance matrix $S$를 이용하여 간단하게 표현이 가능해진다.

여기서 다시 $\bar{x}$ 는 average이고, $(x_n-\bar{x})(x_n-\bar{x})$는 각 data point의 covariance를 의미한다. 그래서 $S$는 covariance의 average가 된다. 그러면 이제 maximum variance를 수식으로 적을 준비가 되었다. PCA를 수행하는데 있어 첫번째 관점으로 variance를 최대로 만들기 위해서 이를 수식으로 보자는 것이다.

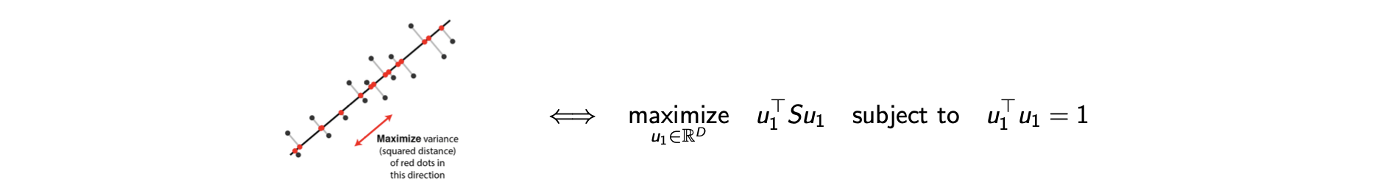
$u_1^Tu_1=1$ 라는 constraint가 없으면 trivial solution을 가지게 된다. 즉, unbounded maximization 문제가 되어서 $u_1$이 무한하게 정의가 될 것이다. 그래서 이 constraint가 필요한 것이다. 그리고 모든 것이 quadratic linear하기 때문에 $u_1$ 을 찾기 위해서 Lagrangian method를 이용해야 한다.

여기서 KKT의 stationay condition을 이용해서 optimal solution을 찾을 수 있다.

여기서 $\lambda_1$은 1차원에서의 scalar이고, $S$는 $D\times D$ 차원의 matrix이다. 이는 곧 linear algebra의 내용으로 $\lambda_1$은 covariance matrix $S$의 eigenvalue가 된다. 즉, variance을 최대로 하는 PCA는 가장 큰 eigenvalue에 대응되는 data covariance matrix의 eigenvector를 계산하는 것과 같다. $Su_1=\lambda_1u_1$ 로부터 $u_1$이 반드시 covariance matrix $S$의 eigenvector여야 하고 eigenvalue로 $\lambda_1$을 가지게 된다. 이 사실을 기반으로 우리의 objective function인 $u_1^TSu_1$ 이 $\lambda_1 u_1^Tu_1$으로 대체될 수 있고, 이는 다시 $u_1^T u_1$이라는 조건에 의해서 $\lambda_1$이 된다. 여기서 우리가 원하는 것은 objectiv function을 최대로 하는 것인데, 이 objecitve가 $\lambda_1$이므로 우리는 PCA와 eigenvector에 대응하는 eigenvalue를 계산하는 것 사이의 상관관계가 있음을 결론지을 수 있다.

M-dimensional Principal Subspace

이전까지 1차원에서 설명했다면 이를 확장해서 지금부터는 $M$을 일반화 시켜보자. 이제 $M$차원으로 projection하는 것은 matrix $U=[u_1,u_2,\dots,u_M] \in R^{D\times M}$로 설명할 수 있다. $U$는 $M$개의 column vector로 이루어져 있고, 각 column vector는 orthonormal column vector이다. 여기서 orthonormal column vector라는 것은 다음의 조건을 만족하는 vector를 의미한다.

$i,j$가 동일한 경우에만 내적 값이 1이 된다. 그러면 이제 maximum variation을 다음과 같이 식으로 나타낼 수 있다.

여기서의 objective는 $M$개의 $u_i^TSu_i$에 대한 summation이 되고, orthonomality를 강제하기 위해서 $M^2$의 constraint를 가지게 된다. $u_i$의 optimal solution을 특징짓기 위해서 Lagrangian method를 이번에도 적용시킬 수 있다. Lagrangian function을 만들고 staitionary condition을 적용하면 $u_i$를 찾을 수 있고, 각 $u_i$는 data covariance matrix의 eigenvector에 대응하고 objective는 대응되는 eigenvalue의 sum이 될 것이다. 그러면 우리는 M차원에서의 PCA는 $M$개의 가장 큰 eigenvalue에 대응되는 data covariance matrix의 eigenvector를 계산하는 것과 같다고 결론지을 수 있다.

그리고 data covariance matrix $S$는 positive semidefinite임을 명심해야 한다. 임의의 vector $v$에 대해서 $v^TSv \geq 0$ 을 만족해야 한다. 이는 $S$가 non-negative eigenvalue를 가진다는 것을 의미하고 objective variance가 양수임을 보장한다. 지금까지 variacne를 최대로 하는 dimensionality reduction의 수식화를 보았고, $M$개의 가장 큰 eigenvalue와 eigenvector를 찾는 것까지 이야기했다.

Minimum Error Formulation

지금부터는 PCA를 두번째 관점으로 보고자 하며, dimensionality reduction의 다른 수식을 살펴 볼 것이다. 이번에는 dimensionality reduction을 위해서 정보의 손실을 최소로 하는 것에 초점을 맞출 수 있다. 즉, projection error를 최소로 하고 싶은 것이고 이를 위해서 data를 다음과 같은 형태로 나타낼 것이다.

각 data는 $D$차원의 orthonormal basis $u_i$의 weighted sum으로 설명할 수 있고, 여기서 weight는 $x_n^Tu_i$로 표현이 ehldj 각 data point에 의존하게 된다. $\alpha_{ni}$의 정의로부터 이를 $x_n$ 식에 대입하면 다음의 결과를 얻게 된다.

그래서 weighted sum이 $x_n$과 같아지게 된다. 만약 $D$차원을 $M$차원으로 감소시킨다고 했을 때, 이는 $i$의 subset을 선택하는 것으로 이해할 수 있다. Basis를 $M$개 선택을 하고 data point $x_n$을 $\tilde{x}$에 의해서 근사시킬 수 있다. $\tilde{x}$는 $M$개의 weighted sum과 나머지의 합으로 주어지게 된다. 전체 $D$차원의 data를 coefficient를 다르게 주어 $M$차원과 나머지로 분리시킨 것이다.

$\sum_{i=1}^M z_{ni}u_i$ 는 incidence-dependent이고, $\sum_{i=M+1}^{D} b_iu_i$ 는 incidence-dependent가 아니다. 여기서 incidence-dependent는 $n$에 의존한다는 것인데, 이는 data point에 의존한다는 의미이다. 즉, 두번째 항을 모든 sample에 대해서 같은 constant로 간주할 수 있다는 것이다. Projection error를 최소로하는 것은 다음과 같이 정리할 수 있다. 우리는 원래 data point와 M 차원의 근사치를 최소화하기를 원한다.

Orthonomal set $\{u_i\}$가 주어졌을 때, $z_{ni}$나 $b_i$에 관한 $J$의 derivative를 0으로 설정하면 우리는 objective $\|x_n-\tilde{x}_n\|^2$ 가 convex한 optimal point를 찾을 수 있다.

$\bar{x}$는 다시 $x$의 mean vector, 혹은 average data point이다. $z_{ni},b_i$를 대입하면 다음과 같이 원래 data point $x_n$과 approximated data point $\tilde{x}$ 사이의 difference를 구할 수 있다. 여기서는 오직 나머지 차원에 대한 difference의 합만 존재한다.
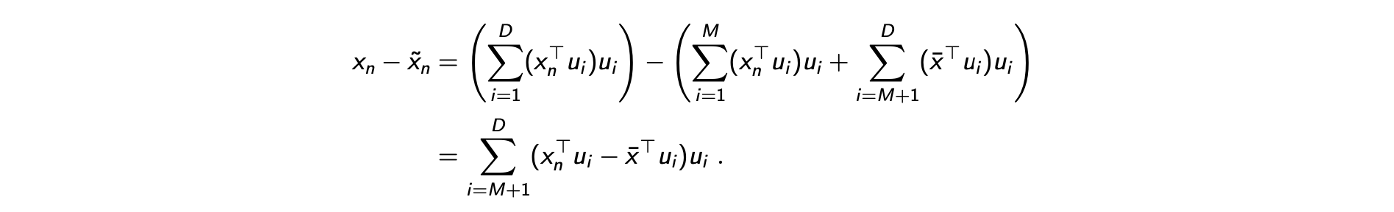이제 이 계산 결과로부터 loss function $J$가 다음과 같이 계산될 수 있다. $J=\frac{1}{N}\sum_{n=1}^N\|x_n-\tilde{x}_n\|^2$ 식에 대입을 한 것이다.

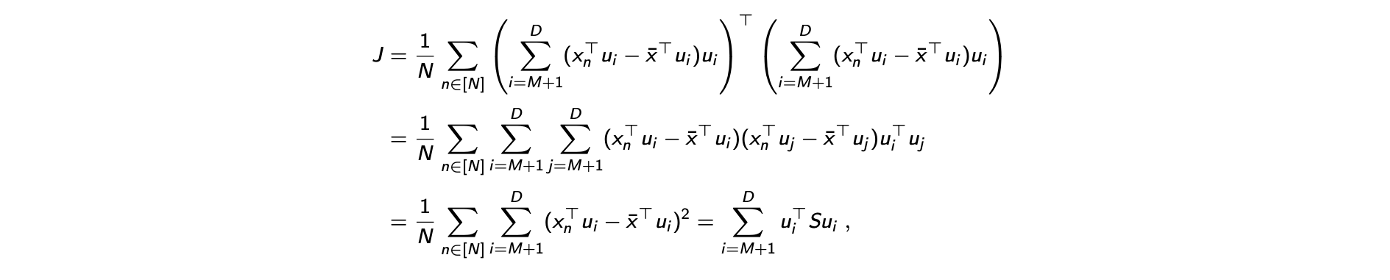여기서 $u_i^Tu_j=\delta_{ij}$를 constraint로 사용하고, 식을 정리하다 보면 이제는 더하는 것은 같지만 $i$의 범위가 $M+1$부터 $D$로 바뀌는 구조가 되었다. 이전에 variance를 최대로 할 때는 1부터 $M$까지 더했지만, projection error를 최소로 하고자 하는 지금은 범위가 달라지게 되었다. 그러면 minimum error forumulation은 다음과 같이 constrained optimization problem으로 정리할 수 있다.

그러면 이를 다시 Lagrangina method를 써서 지금까지 했던 방식대로 구하면 된다. 그러면 우리는 이 minimum error formulation을 eigenvector $u_{M+1},\dots,u_D$ 대응하는 $D-M$ 개의 가장 작은 eigenvalue를 찾는 것과 같다고 결론지을 수 있다. 그리고 이는 $M$개의 가장 큰 eigenvalue와 eigenvector가 $u_1,\dots,u_M$에 대응된다는 것을 의미한다.

그래서 variance를 최대로 하는 것과 error를 최소로 하는 것은 같은 맥락을 따른다. PCA는 $M$개의 가장 큰 eigenvalue와 대응되는 eigenvector를 찾는 것이고, 일단 eigenvector를 찾게되면 우리는 단지 대응되도록 투영시키면 된다. 이것이 PCA가 하는 일이다. 이러한 PCA는 동시에 minimum error formulation과 maximum variance로 이해될 수 있다. 이제 PCA에서 pricipal component는 $M$개의 가장 큰 eigenvector를 찾는 것으로 이해할 수 있다.

An Example of PCA

원래의 image가 $28\times 28$이기에 space의 차원은 $D=28\times 28= 784$가 된다. 그리고 $M$을 위와 같이 설정했을 때 dimensionality reduction의 결과들이다. 결과들을 보면 약 3배정도 차원을 줄인 결과가 noise가 조금 있더라도 크게 다르지 않음을 볼 수 있다. 놀랍게도 1차원으로 줄여도 feature는 많이 잃어버릴 수는 있지만 손글씨를 이해하는데 있어서 어느정도 같은 3이라고 인식할 수 있다.

PCA for High-dimensional Data

세상에는 많은 data들이 있지만 몇몇 data는 PCA를 통해서 dimensionality reduction을 필요로 한다. 이러한 필요성은 특히 high-dimensional data일수록 커지며, 일반적으로는 PCA를 수행하기 위해서는 eigenvalue decomposition을 통해서 eigenvector를 찾을 필요가 있다. 그러나 이때 $O(D^3)$의 computational cost를 필요로 한다. 여기서 covariance matrix $S$는 $D\times D$ 차원이고, decomposition을 하려는 matrix의 크기도 상당히 커서 compuationally intractable 하다. 사실상 data의 개수가 100개로 적은 양이어도 차원 수 때문에 다루기 어려운 것이다. 그런데 여기서 covariance matrix $S$에 대응하는 eigenvalue가 적어도 $D-N+1$개의 값이 0인 eigenvalue를 가진다는 것을 알고 있다.

그래서 지금부터는 data의 개수에 비해서 차원의 수가 큰 경우에 이러한 복잡한 computational cost를 줄이는 방법에 대해서 알아볼까 한다. 먼저 $X$를 $N\times D$ 차원의 centered data matirx로 정의할 것이다. $N$개의 row는 각각 $(x_n-\bar{x})^T$이며 $N$은 data의 총 개수이고 각 row는 $D$ 차원이다. 이러한 notation으로부터 covariance matrix $S$가 $\frac{1}{N}X^TX$ 임을 쉽게 확인 할 수 있다. 왜냐하면 $S$의 정의가 $\frac{1}{N}\sum_n(x_n-\bar{x})(x_n-\bar{x})^T$이기 때문이다. 단지 outer product를 조작해서 notation $X$를 얻은 것이다. 그러면 이제 PCA를 통해서 $X^TX$의 eigenvector를 찾을 것이다. 그래서 우리는 다음의 식을 풀어서 eigenvector를 찾는 것을 목표로 할 것이다.

지금부터는 차원을 줄이기 위해서 몇가지 trick을 사용할 것이다. 먼저 $X$를 곱해주면 다음과 같다. 여기서 $\frac{1}{N}$과 $\lambda$는 scalar이기에 다음과 같이 식을 적을 수 있다. 여기서 $Xu_i$를 따로 분리시켰다.

그러면 이제 이 식은 다루기 쉬워지게 된다. 왜냐하면 $u_i$를 찾아야 하는데는 어려움이 있지만, 식을 변형하면서 대신에 $Xu_i$를 쉽게 찾을 수 있게 된다. $XX^T$는 $N\times N$차원이 되기 때문에 computational cost적인 측면에서 매우 괜찮은 상황이 되었다. 원래 가장 처음 식은 $D\times D$차원의 $S$ 대문에 computational cost가 너무 커서 다루기 어려웠는데, 식을 바꾸게 되면서 $u_i$를 찾는 것보다 $Xu_i$를 찾는 것이 더 쉬워지게 되었다. 이제 그래서 $Xu_i$를 $v_i$로 치환할 것이고, $v_i$에 대해서 쉽게 계산이 끝난 후에 $u_i$로 바꿀 예정이다.

이렇게 식이 바뀌면 $v_i$를 찾는데 있어서 오직 $O(N^3)$ complexity만을 사용하게 된다. 처음에 data의 개수 $N$에 비해서 차원 수 $D$가 월등히 크다고 가정했기에 $D$와 관련된 complexity와 비교했을 때 이는 매우 효율적으로 바뀌게 되었다. 그래서 $v_i$를 계산하고 나면 $v_i$를 다시 우리가 원래 구하고자 했던 $u_i$로 변환해야 한다. 이는 non-trivial 할 수 있지만, 식에다가 다시 $X^T$를 곱해주는 trick을 사용하면 $v_i$로부터 $u_i$를 복원할 수 있게 된다.

이렇게 하면 $X^Tv_i$가 constant이고 $u_i$에 대응할 수 있다. 그래서 $v_i$로부터 $u_i$를 구할 수 있게 되며, 이를 요약하자면 constant를 잘 구하고 나면 매우 높은 차원에서의 PCA를 수행할 수 있게 된다는 것이다. 그래서 $XX^T$의 eigenvector $v_i$를 얻고 normalized eigenvector $u_i$를 $S$에 대해서 계산하면 다음과 같다.

$X^T X$에 대해서 PCA를 수행하기 보다는 $XX^T$의 $N$개의 가장 큰 eigenvector를 얻을 것이다. 그리고 $v_i$를 위와 같이 $u_i$로 변형시킬 것이다. $\frac{1}{N}X^TX(X^Tv_i) = \lambda_i(X^Tv_i)$ 로부터 $u_i$가 단지 $X^Tv_i$라는 것을 알 수 있고, 앞의 항은 정규화를 시켜준 것이다.