[기계학습] Expectation Maximization (EM)

JAEYOON SIM·2021년 11월 15일

Machine Learning

목록 보기

27/35

Estimation with Latent Variables

EM algorithm은 일부 variable이 observable하고 일부는 latent인 경우에 유용하게 사용된다. 왜냐하면 만약 모든 variable이 observable 하면 간단하게 likelihood form을 가지게 되어 추가적인 접근법이 필요가 없기 때문이다. Machine learning에서 모든 어려움은 latent variable로부터 생긴다. Latent variable을 가지고 likelihood를 최적화 하려고 하는 것은 marginalization을 필요로하게 된다. 우리는 EM algorithm의 일반적인 framework로 observable variable과 latent variable이 주어졌을 때 complete data likelihood $p(x,z|\theta)$ 를 적는 법을 알고 있다. 그래서 EM algorithm을 다른 probabilistical model에 적용할 수 있고, 이는 매우 유용하다.

p(x|\theta) = \int p(x,z|\theta)\mathrm{d}z

여기서 $z$ 는 latent variable이다. 그래서 likelihood $p(x|\theta)$ 를 최적화 하는데 어려움이 있다. 왜냐하면 marginalization이 필요하기 때문이다. 만약 $z$ 가 binary random variable이고 $N$ 개를 가지고 있다면, marginalization을 수행하기 위해서 $2^N$ 개의 summation을 가지게 되고, 이는 computaionally intractable하다.

Machine learning에서 우리는 이렇게 다루기 힘든 경우를 피하기 위해서 여러 framework를 사용하게 된다. 이렇게 피하는 방법을 variational inference라 하고 이는 marginalization이나 maximization을 근사하는데 사용이 된다. 우리는 이전에 loopy belief propagation을 배웠고, 이 방법은 variational inference 중 하나이다. 그리고 이번에 자세하게 다룰 EM algorithm도 variational inference 중 하나이다. 이외에도 여러 방법들이 존재한다.

EM algorithm을 이해하기 위해서는 수학적인 지식이 필요하고 이에 대해서 먼저 이야기하고 본격적으로 EM algorithm을 다룰 것이다. 사실 EM algorithm을 approximation algorithm이지만, 우리는 어떠한 다른 approximation을 사용하지 않는다. 그러나 적어도 우리는 optimal solution을 가지기 위해서 convergence는 가져야 한다. 그래서 EM algorithm은 여러가지 성질을 가지고 있고, 이를 이해하기 위해서 먼저 수학적인 지식을 채울 것이다.

Convex Set and Function

먼저 convexity의 정의에 대해서 알아보고자 한다. Convexity는 set뿐만 아니라 function에 대한 성질을 가지게 된다.
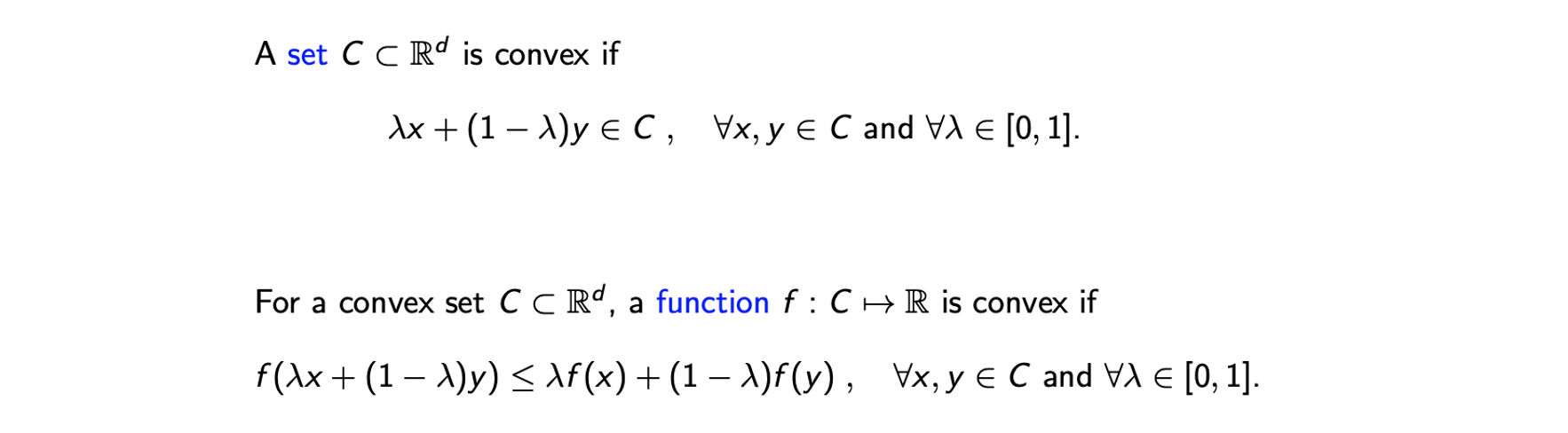D차원에 존재하는 set $C$ 는 어떠한 $x,y$ 를 선택하더라도 위와 같이 convex combination이 다시 set $C$ 에 있는 경우에 convex하다. 만약 2차원인 경우에는 set에서는 2개의 지점을 연결했을 때, 연결한 선이 다시 $C$ 안에 존재하면 된다. 그리고 convex function은 위와 같이 정의가 되는데, function의 domain이 convex set C이고 실수값을 가지는 function일 때 위와 같은 조건 식을 만족한다면 이 function을 convex라고 한다. $x,y$ 의 convex combination의 $f$ 가 $f$ 값의 convex combination보다 작은 경우에 대해서 function이 convex하다고 할 수 있다.

Jensen's Inequality

이러한 convexity를 이용해서 누군가가 흥미로운 inequality를 이야기했다. 바로 Jensen's inequality이고, 이는 여러 버전이 존재하는데 이번에는 random variable에 대한 Jensens's inequality를 이야기해보려고 한다.
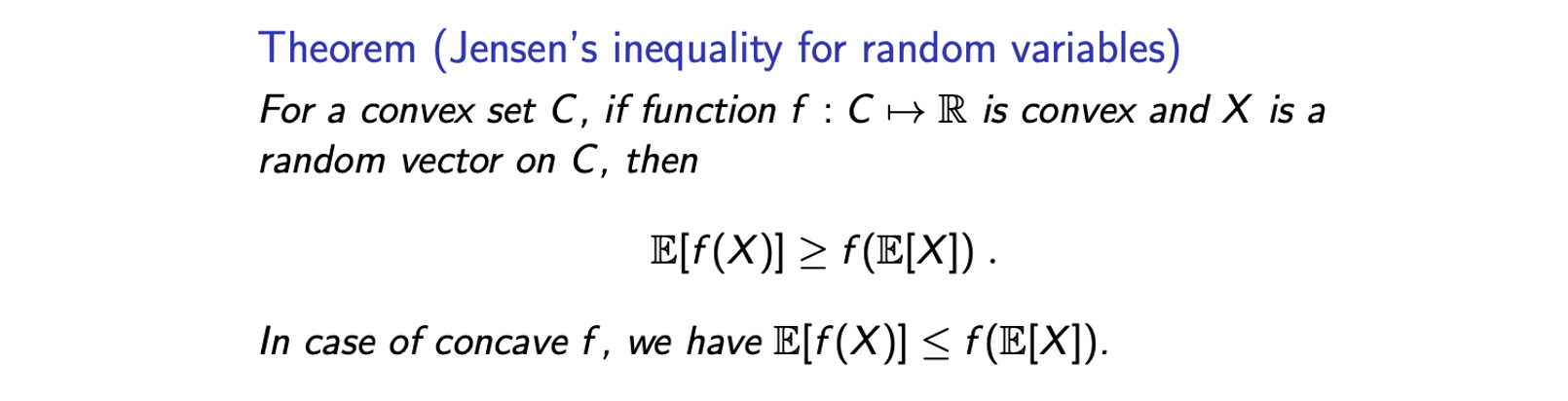만약 $f$ 가 convex하고 $X$ 가 $C$ 에 대한 random variable의 vector일 때 위의 inequaltiy를 만족하게 된다. Function의 expectation이 expecataion의 function보다 크거나 같다. 만약 function $f$ 가 concave하다면, 부등호의 방향은 반대가 될 것이다.

Proof of Jensens' Inequaltiy

증명을 쉽게하고자 discrete random variable $X$ 를 가정할 것이다.
Jensen's inequality를 증명하기 위해서 우변의 식을 먼저 정리할 것이다. 우변의 input은 $x_1$ 에 대한 첫번째 항과 나머지로 분해가 가능하고, 이를 자세히 보면 $p_1$ 과 $1-p_1$ 을 더하면 1이 되기에 또 다른 convex combination이 되었다. 그래서 convexity를 이용해서 첫번째 부등식을 만들 수 있다. 그리고 다시 두번째 항을 $x_2$ 에 대한 항을 따로 분리해서 분해할 수 있다. 그러면 $x_2$ 와 나머지 항들의 convex combination 형태가 만들어진다. 그리고 여기 다시 Jensen's inequality를 이용해서 부등식을 만들 수 있고, 이러한 과정을 계속해서 반복할 수 있다. 그래서 결과적을 $\sum p_i\cdot f(x_i)$ 의 식으로 정리가 가능해서 Jensen's inequality를 증명할 수 있게 된다. 우리는 이 Jensen's inequality를 이용해서 KL divergence를 보여줄 것이다.

Information and Entropy

이제 다시 infromation과 entropy의 정의를 기억해보고자 한다. Random variable $X$ 의 information은 probability의 negative log가 된다. 이는 uncertainty나 surprise를 수치화하는데 사용된다. 만약 $p(X) = k$ 로 작아지면 이는 매우 놀라운 일이라는 것이고, 이는 information $I(x=k)$ 를 증가시킨다. Entropy는 information의 expectation으로 entropy는 data $X$ 를 나타내기 위해서 bit의 개수를 수치화한다.

Entropy and Relative Entropy

KL divergence는 distribution $p$ 대 reference distribution $q$ 의 relative entropy를 측정하는 것이다.

\text{KL}(p||q):=\sum_{x\in\mathcal{X}}p(x)\text{log}\frac{p(x)}{q(x)}

Gibb's Inequality

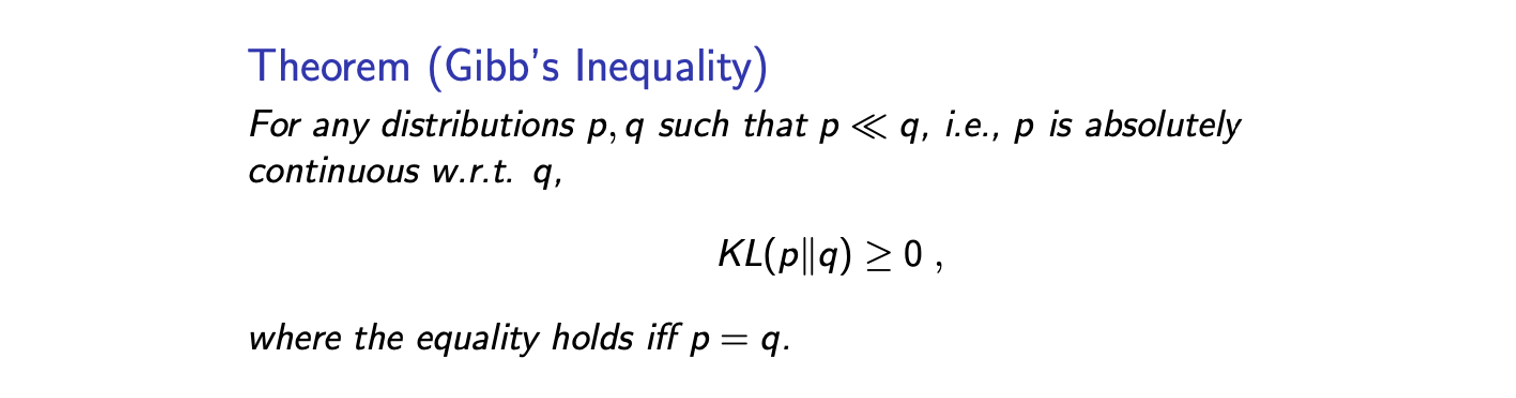Gibb's inequaltiy는 어떠한 distribution $p,q$ 에 대해서도 KL divergence의 non-negativity를 보장해준다. 수학적인 회귀를 위해서 우리는 $q$ 에 대해서 $p$ 가 absolutely continuous한 KL divergence의 유효한 값을 가질 수 있는 조건이 필요하다. 그리고 $q(x)=0$ 이면 $p(x)=0$ 이 된다. 이는 우리가 $\epsilon \times log\frac{\epsilon}{0}$ 의 시간이 무한대로 발산하는 것을 피하도록 해준다. 그래서 우리는 KL divergence의 lower bound로 0을 가지게 된다. 증명은 random variable에 대한 Jensen's inequality를 이해했다면 매우 간단하다.
KL divergence는 우리가 discrete random variable을 가정했을 때 위와같이 적을 수 있다. 물론 continuous variable로 확장시킬 수 있지만, 간단함을 위해서 discrete distribution이라 가정할 것이다. 그러면 이 distribution을 negative를 붙여서 분자 분모를 바꿔서 다시 적을 수 있다. 그러면 이 식은 log function의 weighted sum으로 이해할 수 있고 Jensen's inequality를 이용해서 부등식을 만들 수 있다. 여기서 negative log는 convex하기 때문이다. 그러면 $p_i$ 는 지워지고 $q_i$ 의 합은 1이기에 결과적으로 0이 된다. 그리고 추가적으로 "equality hods iff p = q"라는 statement가 존재한다. 그리고 이 statement는 또 다른 증명이 필요하다.

Gibb's Inequality: Proof of the Equality

이를 위해서 lower bound를 확인하고자 KL divergence를 최적화하고자 한다.

\mathcal{F}(p,\lambda)=\text{KL}(p||q)+\lambda(1-\sum_i p_i)=\sum_i p_i\text{log}\frac{p_i}{q_i}+\lambda(1-\sum_i p_i)

$p$ 가 distribution이기에 우리는 $\sum_i p_i=1$ 이라는 constraint를 가지게 되고, 이는 constraint optimization이 된다. 그래서 lagrangian $\lambda$ 는 constraint이다. KL divergence의 최소값이 무엇인지 알기 위해서 KKT condition 중에서도 stationary condition을 사용할 것이다.

\frac{\partial \mathcal{F}}{\partial p_i}=\text{log }p_i+ \text{log }q_i + 1 - \lambda = 0

이는 각 $i$ 에 대한 $p_i=q_i \text{ exp}(\lambda - 1)$ 을 나타내고, constraint $\sum_i p_i = 1=\sum_iq_i \text{ exp}(\lambda - 1)$ 을 이용하면 $\lambda=1$ 이 된다. $\text{exp }(\lambda -1)$ 이 증가하고 $\sum_i q_i=1$ 이라는 조건을 이용하면 우리는 $\lambda$ 가 반드시 1이 된다고 결론지을 수 있다. 그래서 반대로 $\lambda=1$ 을 stationary condition에 대입하면, 우리는 $p_i=q_i$ 가 KL divergence의 유일한 minimal인 것을 결론낼 수 있다. 그리고 이는 만약 $\text{KL}(p||q)=0$ 이면, 어디서든 $p_i=q_i$ 임을 나타낸다. 이렇게 equality를 증명할 수 있다.

그렇다면 왜 이런 Gibb's inequality와 같은 것을 배우는 것일까?

A Lower Bound on the Log-Likelihood

EM algorithm은 우리가 $x$ 가 observed variable, $z$ 가 latent variable, $\theta$ 가 model parameter인 경우에 $p(x,z(\theta))$ 를 쉽게 나타낼 수 있을 때 사용한다. 그러나 $p(x|\theta)$ 를 나타내는 것은 어렵다. 왜냐하면 latent variable $z$ 를 marginalization하는 것은 computationally intractable하기 때문이다. 그래서 $\theta$ 에 대해서 최적화를 하는 것은 true likelihood $\mathcal{L}(\theta)$ 이다.

\mathcal{L}(\theta) = \text{log }p(x|\theta) = \text{log }\int p(x,z|\theta)\mathrm{d}z

이 식은 latent variable $z$ 가 있어서 쉽게 최적화를 하기 어렵다. 우리가 하고자 하는 것은 log-likelihood를 최대화하는 것이다. 만약 ㅣog-likelihood의 lower bound에 대해서 다루기 쉬운 형태가 있다면 어떠할까? 그러면 이 lower bound를 최대화하는 것에 초점을 맞출 수 있고, 최적화 방향이 자연스럽게 lower bound보다 큰 true likelihood로 증가할 것이다. 이러한 직관을 이용해서 distribution $q(z)$ 를 보고자 한다. 어떠한 distribution $q(z)$ 가 주어지더라도 다음의 inquality를 만족할 것이다.

\mathcal{L}(\theta)=\text{log }\Bigg(\int q(z)\frac{p(x,z|\theta)}{q(z)}\mathrm{d}z\Bigg) \geq \int q(z)\text{log }\Bigg(\frac{p(x,z|\theta)}{q(z)}\Bigg)\mathrm{d}z\qquad\text{(Jensen's ineq)}

log는 concave function이기에 Jensen's inequality를 사용할 수 있다. 그리고 $\mathcal{F}(q,\theta)$ 에 의해서 lower bound를 나타낼 수 있다.

\mathcal{F}(q,\theta):=\int q(z) \text{log }\Bigg(\frac{p(x,z|\theta)}{q(z)}\Bigg)\mathrm{d}z = \int q(z)\text{log }p(x,z|\theta)\mathrm{d}z + H(q) \qquad\text{Def. of entropy}

이 lower bound는 분자 항과 entropy 항으로 분해할 수 있다. 여기서 entropy는 오직 $q$ 에 대한 function이다. 그래서 M-step에서 entropy 항을 제외하고 첫번째 항에만 집중해도 된다. 대략적으로 EM algorithm이 하는 일은 다음과 같다.
E-step에서는 lower bound를 더 엄격하게 하기 위해서 $q$ 에 관한 lower bound $\mathcal{F}(q,\theta)$ 를 최대로 하고, M-step에서는 $q$ 를 고정으로 하고 $\theta$ 에 관한 lower bound $\mathcal{F}(q,\theta)$ 를 최대로 한다. EM algorithm은 이 과정을 반복해서 진행한다.

EM Algorithm with Max-Max Interpretation

EM algorithm은 이렇게 max-max algorithm이고 E-step에서는 $q$ 에 대해서 lower bound를 최대로 하고 M-step에서는 $\theta$ 에 대해서 lower bound를 최대로 한다.
여기서 complete log-likelihood $\text{log }p(x,z|\theta)$ 는 전형적으로 다루기 쉽게 매우 아름답게 사용된 형태이다. 서로 다른 $q$ 를 가짐으로써 이전보다 더 쉽게 계산이 가능해진다.

Monotonicity of EM Algorithm

이제 이러한 max-max algorithm은 true log-likelihood를 개선할 수 있고, 이는 다음의 statement에 의해 도움을 받는다.
EM algorithm은 단조롭게 true log-likelihood를 개선한다. 이를 확인해보고자 true log-likelihood $\mathcal{L}(\theta)$ 와 lower bound $\mathcal{F}(q,\theta)$ 간 difference를 볼 것이다. 첫번째 등호는 정의로부터 온 것이고 두번째 등호는 Bayes rule에 의한 것이다. 세번째 등호는 식을 분해하고 지우면서 간단하게 만든 것이다. 결과적으로 KL divergence로 정리가 되었다. 우리는 KL divergence가 $q(z)=p(z|x,\theta)$ 가 Gibb's inequality에 의해서 0인 사실을 알고 있다. 이는 E-step이 발견한 것이다. E-step은 $q(z)$ 를 최적화하려고 시도했다. 이러한 계산으로부터 우리가 알수 있는 사실은 Gibb's inequality를 사용해서 E-step이 $q(z)=p(z|x,\theta)$ 를 발견해야 한다는 것이다. 이러한 모든 사실로부터 마지막 식을 얻을 수 있다. 그래서 이는 EM algorithm의 monotonicity를 설명하게 된 것이다. $\theta^{(k)}$ 의 log-likelihood가 $k+1$ 번째에서 개선이 되는 것이다.

EM Algorithm

요약하면 EM algorithm은 다음과 같다. E-step에서는 $\mathcal{Q}$ 를 계산할 것이고, $\mathcal{Q}$ 는 observed variable $x$ 와 이전에 예측된 $\theta$ 가 주어졌을 때 latent variable $z$ 에 대한 marginal probability이다. E-step은 M-step을 위한 준비 과정이다. M-step에서는 $\mathcal{Q}(\theta;\theta^{(k)})$ 를 $\theta$ 에 대해서 최적화 하려고 시도한다.

EM alogorithm은 variational Bayesian inference이고 쉽게 likelyhood나 marginalization을 계산하기 어려울 때 사용할 수 있다. Convergence에 도달할 때까지 E-step과 M-step을 반복적으로 시행하면 된다. E-stpe에서는 complete data log-likelihood의 expectaion을 계산해준다. 즉, latent variable $z$ 와 observed variabel $x$ 의 likelihood를 통해서 계산하는 것이다. Expectation은 $z$ 에 대해서 observing하지 않을 것이기에 latent variable $z$ 에 대해서 대체되어서 $z$ 를 approximation하거나 marginalization을 할 수 있다. E-step에서 계산을 마치면 $\mathcal{Q}$ 가 생기고, 이를 이용해서 M-step에서 parameter를 찾을 것이다. Expectation을 최대로 만드는 $\theta$ 를 찾고 싶은 것이다. 이러한 과정 속에서 EM algorithm의 monotonicity라는 이론적 보장성을 받는다.

Generalized EM: Partial M-steps

EM algorithm의 일반적인 변형과 예시들이 존재하는데, EM algortihm의 변형 중 하나로 M-stpe을 부분적으로 업데이트 할 수 있다. M-stpe은 maximization solution을 찾는 과정이다. 그러나 maximization은 복잡한 계산을 필요로 한다. 매우 커다란 neural network를 여기서 $\theta$ 로 생각하면 된다. 이 경우에 maximization은 gradient descent에 있어 여러번의 epoch을 필요로 하기에 계산이 엄청 복잡해진다. 그래서 convergence를 찾기보다는 gradient descent 혹은 ascent에서 부분적으로 몇 단계만을 생각해볼 수 있다. 이러한 변형을 partial M-step이라고 부르고, 이것이 M-step을 대체할 수 있다. Monotonicity 덕분에 partial M-step과는 상관없이 $\mathcal{L}(\theta^{(k)}) = \mathcal{F}(q^{(k+1)},\theta^{(k)}) \text{ at E-step }$ 이 타당하고, 만약 partial M-step을 대입하면 여전히 $\mathcal{L}(\theta^{(k)}) = \mathcal{F}(q^{(k+1)},\theta^{(k)}) \text{ at E-step } \leq \mathcal{F}(q^{(k+1)},\theta^{(k+1)}) \text{ at M-step }$ 과 같이 inequality가 성립한다. 왜냐하면 비록 이것이 최대라고 할지라도 $\theta^{(k)}$ 가 $\theta^{(k+1)}$ 로 개선이 될 것이기 때문이다. 또한 $\mathcal{F}(q^{(k+1)},\theta^{(k+1)}) \leq \mathcal{L}(\theta^{(k+1)})$ 과 같이 Jensens' inequality 또한 적용이 될 것이다. 비록 우리가 partial M-step을 진행할지라도 여전히 partial EM alogirhtm의 monotonicity를 증명할 수 있다. 이것이 요즘 model 크기가 커서 자주 사용되는 방법이다.

Exponential Family

지금부터는 EM algorithm의 일반적인 식에 대해서 알아보려고 한다. 우리는 exponential family에 대해서 알아볼 것이고, 여기서 familiy가 의미하는 것은 probability distribution이다. Likelihood가 다음과 같은 형태일 때 우리는 이를 exponential family라고 할 것이다.

p(x|\theta)=h(x)g(\eta)\text{exp}(\eta^Tu(x))

Model $\theta$ 가 주어졌을 때 variable $x$ 의 probability는 여러 function들의 곱셈 형태로 보기에는 복잡해 보일 수 있다. 이 형태는 어디에나 사용이 가능하다. 더 나은 이해를 위해서 각 function의 정의를 알아보도록 하자. $g(\eta)$ 는 다음과 같이 1로 만드는 normalization factor이다.

\int p(x|\theta) \mathrm{d}x = g(\eta)\int h(x)\text{exp}(\eta^Tu(x)) \mathrm{d}x = 1

$p(x)$ 가 probability distribution이고 $g(\eta)$ 일종의 normalization factor이기에 위의 식은 1이어야 한다. 위의 식이 다소 복잡해보일 수 있으나 대부분 이미 알고 있는 probability distribution으로부터 찾을 수 있다. 하나의 예시로 Bernoulli를 보도록 하자. Bernoulli distribtuion은 exponential family의 예시로 정의에 의해서 다음과 같이 적을 수 있고, 추가적이로 exponential과 logarithm에 의해서 변형시킬 수 있다.
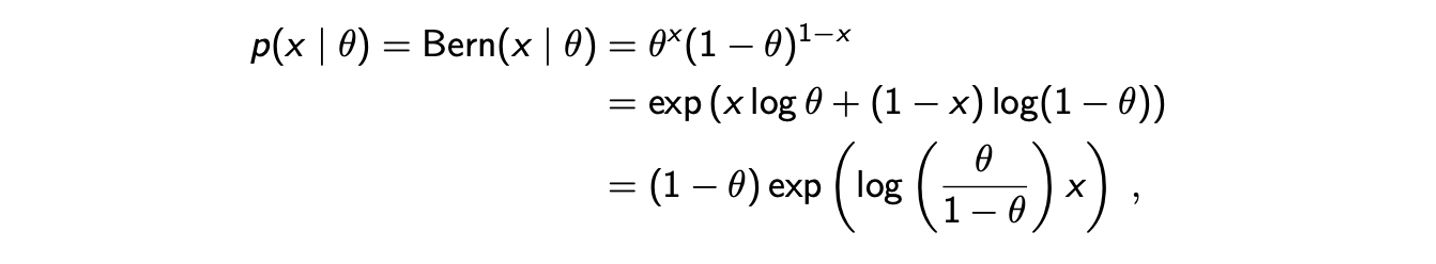이로부터 Bernoulli distribtuion을 exponential familiy로 보았을 때, 다음과 같이 function들을 정의할 수 있다.

\eta = \text{log }\bigg(\frac{\theta}{1-\theta}\bigg),\quad h(x)=1,\quad u(x)=x,\quad g(\eta)=\frac{1}{1+\text{exp }(\eta)}

결과적으로 Bernoulli distribution의 변형된 식은 exponential family의 형태와 일치하는 것을 볼 수 있다. 이외에도 여러 유명한 distribution들이 exponential family가 될 수 있고, 앞서 이야기 했듯이 exponential family는 어디에서나 사용이 가능하다. 그래서 이번에는 EM algorithm에 대해서 exponential family를 보려고 한다. 편의성을 위해서 complete data를 observed variable $x$ 와 latent variable $z$ 로 정의하고자 한다. 그래서 complete data $s=(x,z)$ 이고, 이 complete data는 exponential family에 의해서 modeling 된 것으로 가정할 것이다. 그러면 다음과 같이 E-step에서 계산이 필요할지도 모르는 expected complete-data log-likelihood를 나타낼 수 있다.
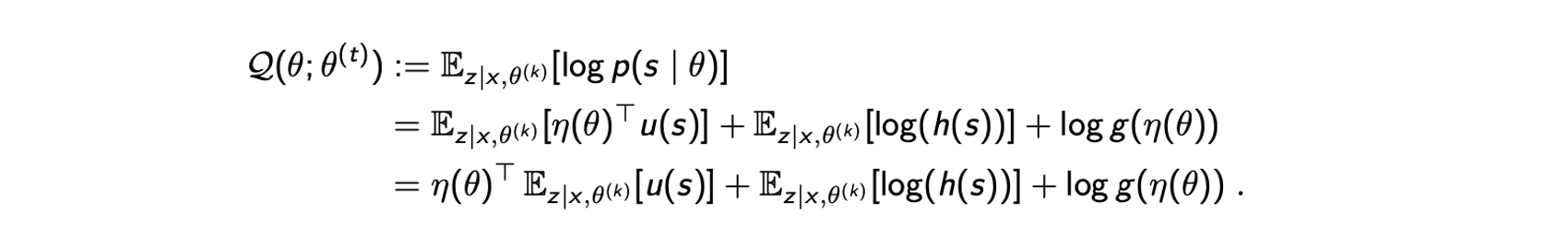첫번째 등호는 정의로부터 온 것이고 두번째 등호는 complete data가 exponentail family라는 가정으로부터 온 것이다. 여기서 $\eta(\theta)$ 는 $z$ 와 independent하다. 그래서 세번째 등호에서 $\eta(\theta)$ 를 밖으로 뺄 수 있다. 그렇게 expected complete-data log-likelihood를 얻을 수 있고, 다음과 같이 간단하게 EM algorithm을 정리할 수 있다.
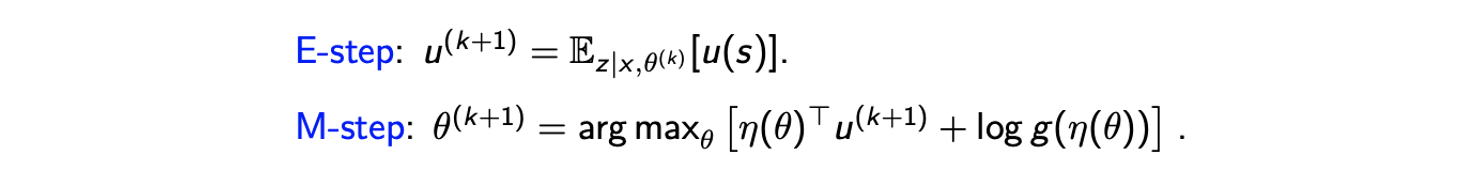E-step에서 $u^{(k+1)}$ 을 구해고 이를 $\mathcal{Q}$ 에 대입해서 complete-data log-likelihood를 최대로 만드려고 할 것이다. 여기서 $E[\text{log}(h(s))]$ 가 왜 사라졌는지 의문일 수 있다. 사실상 이 항은 $\theta$ 에 대해서 constant이다. 물론 식에 $\theta^{(k)}$ 가 있긴 하지만 EM algorithm에서는 이를 다시 고정시켜서 M-step에서 이를 constant로 여길 것이다. 그래서 이 항에 대해서는 계산하거나 최대로 만들 필요가 없다.