[기계학습] Unsupervised Learning: Clustering

Unsupervised Learning

Unsupervised learning의 예로는 clustering, feature selection, dimensionality reduction, generative model 등이 있다. 여기서는 어떠한 label도 가지지 않아서 한계점이 존재한다. 이제부터 하나씩 자세히 보도록 할 것이다.

Introduction of Clustering

Clustering은 unsupervised learning 중 하나로 similarity나 distance measure을 사용해서 label이 없는 data point의 set을 유사한 point나 미리 지정된 수의 그룹으로 분할하는 task이다. Computer vision 중 유명한 적용 분야로는 image segmentation이 있다.

Image Segmentation via Classification

Image segmentation은 image를 여러 partition으로 나눠서 색을 칠하게 된다. 특히 partition은 같은 개체를 묶어서 나타내려고 한다. 좌측의 image에서 사람과 자전거를 나눠서 색을 칠하고 싶은 것이다. 그래서 우측에 사람은 분홍색으로, 자전거는 초록색으로 pixel에 색을 입힌 것이다. 이러한 image segemenation을 classification task처럼 하기 위해서 각각의 pixel이 어떠한 개체에 속하는지 labeling을 해줘야 하기 때문에 아마도 사람들의 많은 노력이 필요할 것이다.

Image Segmentation via Clustering

사람의 경우 해당하는 pixel이 자전거인지 사람인지 알지 못해도 사람은 pixel들을 각 개체에 대해서 clustering 할 수 있다. 이러한 것들은 위의 그림으로 설명될 수 있다. 좌측에 grayscale image가 주어졌을 때 우리는 비슷한 intensity를 가지는 pixel들을 clustering 할 수 있다. 이로부터 우리는 pixel clustering에 대한 image segmentation의 괜찮은 approximation을 보여주는 우측의 image를 얻을 수 있다. 이렇게해서 누군가는 classification을 위한 image segmentation dataset을 만들지도 모른다. 비록 clustering 결과가 완전치 못해 error가 있는 부분이 있을지라도 이는 사람에 의해서 쉬운 방법으로 조절이 가능하다.

그리고 clustering task를 수행하기 위해서 우리는 similarity measure를 조심히 정의해야 한다. Similarity measure이라는 것은 위의 예시에서는 intensity의 distance로 정의할 수 있다. 만약 2개의 pixel에 대해서 비슷한 intensity를 가진다면 같은 cluster로 묶으면 된다. 만약 intensity가 완전히 다르면 이들을 2개의 분리된 cluster로 묶으면 된다. 이러한 식으로 clustering task를 수행하고자 한다면, 어떠한 data point가 비슷한지 생각해서 similarity measure를 조심히 정의할 필요가 있다.

Clustering

Unsupervised learning의 유명한 task는 일부 similarity 혹은 distance measure를 사용해서 label이 없는 data point set을 유사한 point의 미리 지정된 수의 그룹으로 분할하는 것이다. 이전에 clustering은 similarity measure나 distance measure 등이 필요하다고 했었다. 그리고 K-means clustering은 유명한 method 중 하나이다.

A Cost function for Clustering

Clustering algortihm은 최대한으로 많은 수 $K$개의 cluster와 label이 아닌 data point $x_i$들의 set을 input으로 필요로 한다.
이제 우리는 intra variance를 최소로 하고픈 clustering에 대해서 생각해 볼 것이다. Clustering은 data point $i$가 cluster $k$에 속하는지 아닌지를 결정하는 것이고, 여기서 $r_{ik}$를 indicator라고 부를 것이다. 만약 $r_{ik}$ = 1이면 data point $x_i$가 cluster $k$에 속하는 것이다. 그리고 $r_{ik}$는 $\sum_{k\in[K]}r_{ik}=1$이라는 constraint를 가진다. 이 말은 하나의 cluster $k$에 대해서만 1이라는 값을 가져야하고 나머지는 모두 0이어야 한다. 그래서 $r_i$는 다음과 같이 해당하는 cluster의 index에 대해서만 1로 표현이 되는 one-hot vector이다.

이는 매우 자연스러운 가정과 제약이다. 이제 각 cluster $k$에 대해서 $\mu_k$라는 reference point를 가지게 된다. 그러면 우리는 data point가 reference point에 가장 가까운 cluster이기를 원한다. 만약 여러개의 reference point가 있고, 하나의 data point가 $\mu_1$에 가깝게 있다면, 이 data point를 $\mu_1$으로 clustering 할 것이다. 왜냐하면 $\mu_1$이 모든 $\mu$ 중에서 가장 가까운 reference point이기 때문이다.

여기서 우리는 similarity measure로 Euclidean distance를 사용할 것이다. $r_{ik}$와 $\mu_k$를 최적화 함으로써 최소로 만들어야 하는 cost function은 $r_i$와 $\mu_k$ 간 Euclidean distance의 summation이다. 물론 L2-norm을 L1-norm으로, 혹은 일반화해서 Lp-norm으로 원한다면 바꿔도 좋다. 이러한 식으로 similarity measure을 정의하는 것은 distance measure를 정의하는 것과 똑같다. 지금까지 말하고자 했던 것은 clustering을 위해서 cost function의 선택에 대한 것이었다. 원한다면 다른 cost function을 사용해도 되지만, 위에서 정의한 것이 가장 일반적인 경우에 해당한다.

K-mean Algorithm (Informal Description)

위에서 본 식은 다소 복잡해서 computationally expensive하고 intractable하다. 왜냐하면 $\mu$가 continuous space에서의 optimization이기 때문이다. 그리고 두번째 minimization term은 optimal point를 찾기 위해서 searching space가 $K^\mu$에 비례하는 조합을 최적화해야한다.

이러한 $\mu$와 $r$을 동시에 최적화하는 joint minimization problem은 복잡하기 때문에 다음과 같이 K-mean algorithm이라 불리는 방법을 통해서 직관적으로 접근할 수 있다.
2개의 minimization problem에 대해서 우리는 위와 같은 방법을 생각할 수 있다. 먼저 assignment step에서 reference point $\mu$를 고정시키고 optimal assignment $r$을 찾는 것이다. 다음으로 update step에서는 assignment $r$을 고정시키고 새로운 reference point $\mu$를 찾는다. 이 과정을 convergence가 생길 때까지 반복한다. Update step에서 $\mu$를 centroid라고 한 이유는 각 cluster에 대해서 중심을 찾기 때문이다. Centroid는 data set의 중심에 있는 point이며 조금 있다가 정의해보도록 할 것이다. 어쨌든 이러한 과정은 매우 자연스럽고 간단하다.

Example with 2 Cluster

계속해서 K-mean algorithm을 진행한다면 다음과 같은 결과를 얻을 수 있다.
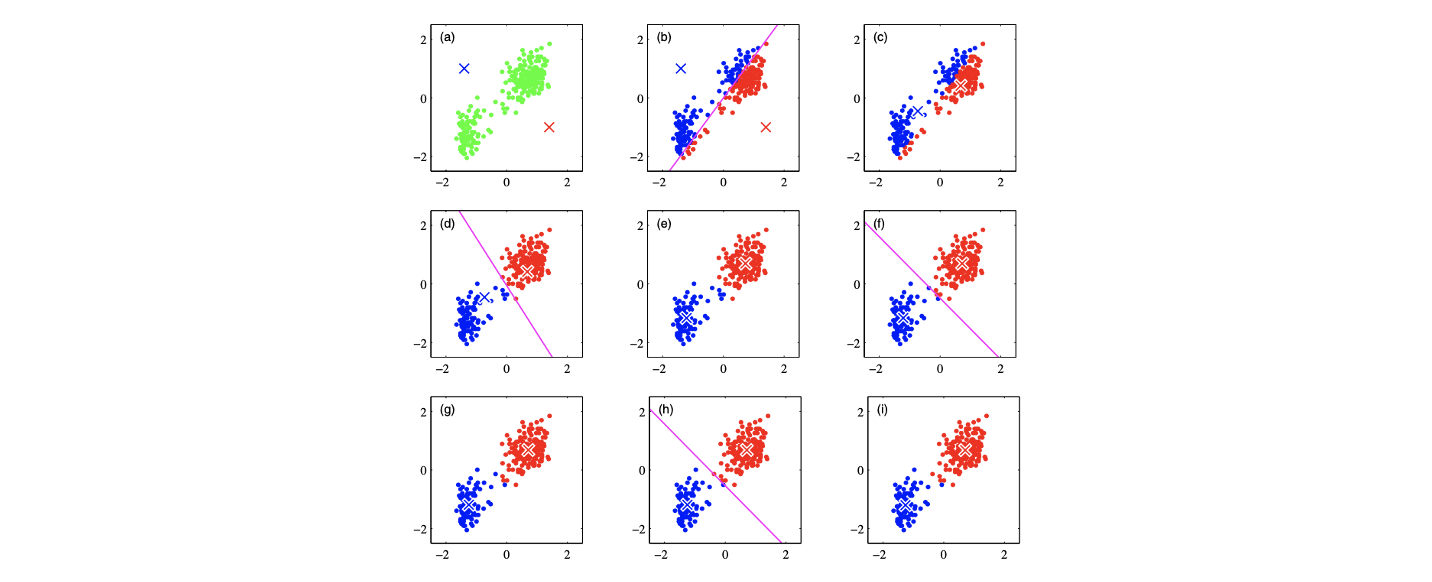첫번째 반복인 (a)에서 reference point $\mu$를 임의로 선택해서 시작할 것이다. 이 point들을 기반으로 data point를 split하고 $r$을 정할 것이다. (b)를 보면 좌측 상단의 reference point를 따라서 파란색 cluster를 만들고 우측 하단의 reference point를 따라서 빨간색 cluster가 만들어지고 seperation bound가 중간에 형성된다. 이렇게 주어진 assignment에 대해서 (c)에서 reference point를 cluster마다 평균인 지점으로 update 하게 된다. 다시 이를 통해서 (d)에서 data point를 분리하고 새롭게 cluster를 만들게 된다. 이러한 방식으로 reference와 seperation bound를 convergence까지 update해가면 최종적으로 (i)와 같은 clustering 결과를 얻을 수 있다. 이 결과는 사람의 눈으로는 매우 자연스러운 결과를 보여준다.
우리가 distance를 RGB space에서 Euclidean distance로 정의했을 때, 위와 같은 image segmentation 결과를 얻을 수 있다. Clustering의 최대 개수가 $K=2$인 경우에는 아직은 애매한 segmentation 결과를 얻게 된다. 만약 $K$가 계속해서 증가한다면 원래의 image와 점점 비슷해지는 clustering 결과를 얻게 될 것이다. K-mean algorithm을 본격적으로 보기 전 간단하게 아이디어를 살펴보았다.

K-means Algorithm

지금부터는 K-means algorithm을 자세하게 알아보도록 할 것이다.
임의로 $K$개의 reference point인 centroid를 선택하는 것부터 시작하고자 한다. 그리고는 assignment step를 진행하는데, 여기서 $r_{ik}$를 위와 같이 정의해준다. $r_{ik}=1$인 경우는 $k$가 $x_i$와 $\mu_k$간 distance를 최소화하는 경우로 해당 data point가 $k$에 속하는 경우를 말한다. 여기서 $\mu$가 주어졌을 때 $r_{ik}$는 위와 같이 선택하면 되고 이는 최적의 cost function임을 쉽게 확인할 수 있다. Update step에서는 위와 같이 $\mu_k$를 assignment step에서 정해진 $r$이 주어졌을 때 update 할 수 있다. $\mu_k$는 cluster $k$에 속한 point의 개수에 대한 cluster $k$에 속한 data point의 summation의 비율이 된다. 즉, cluster $k$에 속한 data point의 평균이 되고, 이것이 바로 centroid로 매우 자연스러운 정의이다. Cost function의 gradient를 0으로 함으로써 reference point를 optimal하게 선택하는 것이다.

비록 각 step이 원래의 cost function을 절반만 optimization하기는 하지만, 이렇게 해서 optimal solution을 구하는 것이 가능하다. 왜냐하면 각 minimization의 domain이 완전히 다르기 때문이다. 하나는 $\mu$에 대해서 continuous space이고, 다른 하나는 $r$에 대해서 일종의 discrete space이다. 각 step에서 우리는 일종의 local optimal point를 구하는 것이다.

Properties of K-means

K-means algorithm은 다음과 같은 성질들을 가지게 된다. 아쉽게도 이 algorithm은 optimal 하지 않다. 이는 local minimum에 빠질 위험이 있다는 것을 의미한다. 각 step에서는 locally optimal하지만, 우리가 원하는 것은 jointly optimal이다. Local optimal point를 가질 수 있는 위험을 제외하고 convergence를 보장할 수 있다. 그리고 이 algorithm은 꽤 빠른편이며 각 step에서는 대략 linear complexity를 가지게 되어 K-means alogrithm은 빠른 clustering에 속하게 된다. 그리고 global optimal을 보장하기 위해서 K-means++와 같은 변형된 algorithm을 생각할 수 있는데, 이는 K-means와 같다고 생각하면 되지만 intial point를 좀 더 정교하게 선택하게 된다.

Limitation of K-means

다음은 local minima 외에 또 다른 limitation이다. 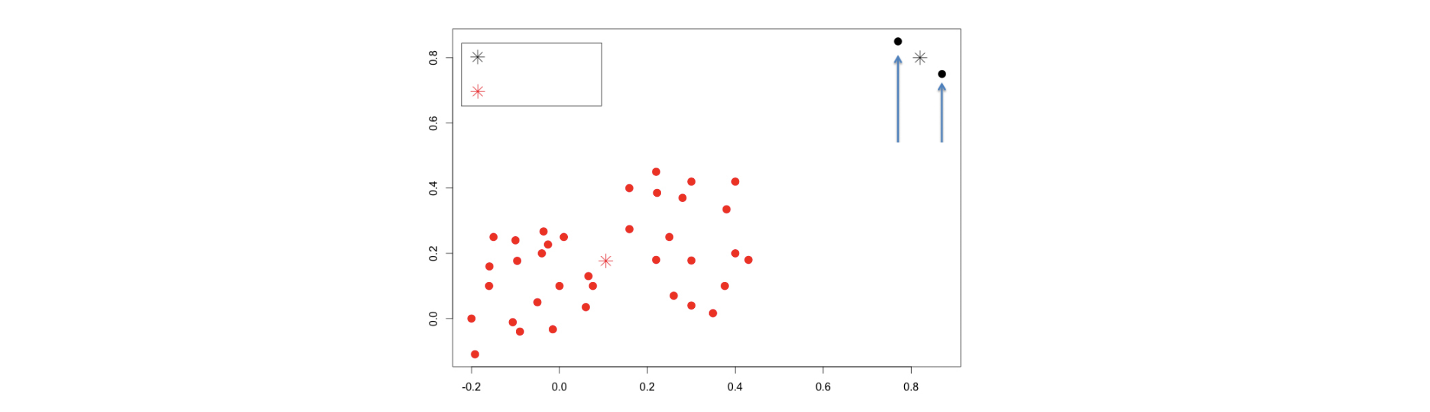K-means algorithm은 위와 같이 dataset을 가졌을 때 outlier에 매우 sensitive하다. $K=2$인 경우에는 outlier를 포함해서 하나의 cluster를 만들어야 한다. 하지만 outlier는 매우 작은 부분이기에 이를 제외하고 싶을 것이다. 그러나 아쉽게도 K-means algorithm은 빨간 data point들을 하나의 cluster로 하고 outlier들을 하나의 cluster로 나눌 것이다. 현실에서는 outlier가 상당히 많이 존재하지만, 여기서 우리가 원하는 결과는 outlier를 제외하고 clustering 하는 것이다.

K-medoid

이러한 outlier를 무시하기 위해서 K-medoid algorithm이 등장했다. 이 algorithm은 실제 data point로부터 referecence data point를 선택하게된다.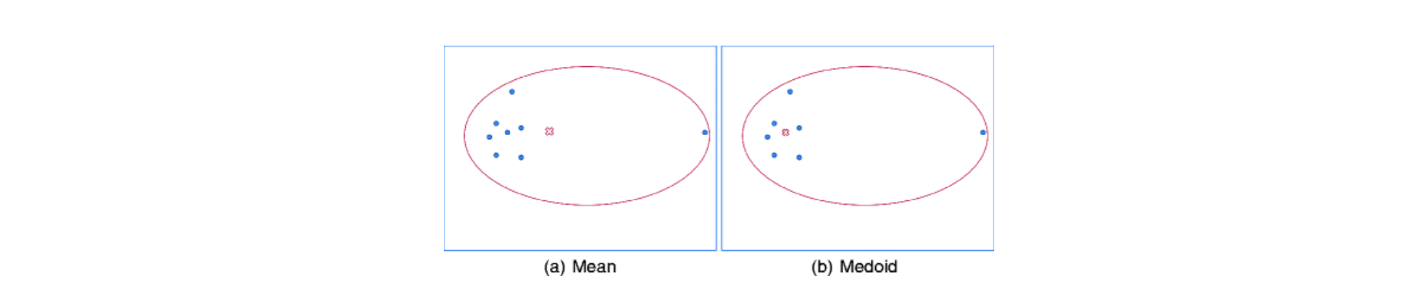 위와 같이 data point들이 주어졌을 때, K-means는 outlier의 영향을 받아서 좌측과 같이 reference point를 설정하게 된다. 반면 K-medoid는 Euclidean distance를 최소로 하는 actual data point를 우측과 같이 reference point로 설정할 것이다. K-means와 비교해서 K-medoid는 outlier에 꽤 robust하다.

Soft K-means

K-means에서 또 다른 limitation으로는 soft-labeling이 존재하지 않고, 모든 것이 매우 hard하게 결정이 되었다. 이는 one-hot vector를 사용해서 1과 나머지는 0을 사용해서 생기는 문제점이다. 우리가 원하는 것은 0과 1로 나누는 것이 아닌 0에서 1사이의 값들로 나누고 싶은 것이다. 그래서 K-means를 확장해서 soft clustering이 가능한 soft K-means를 생각했다. Soft clustering에서는 더이상 vector $r_{ki}$가 one-hot vector가 아니고, 이것을 기점으로 soft K-means가 확장되었다. Soft K-means algorithm도 assignment step와 update step이 존재한다. Assignment step에서는 $r_{ki}$를 위와 같이 update한다. 만약 $\beta$를 무한대로 보낸다면 $r_{ki}$를 hard assignment로 근사할 수 있다. 그러나 지금은 $\beta$를 finite으로 가정할 것이고, $r_{ki}$가 주어졌을 때 update step에서 새로운 centroid를 위와 같이 구할 수 있다. $r_{ki}$가 더이상 one-hot vector가 아니기에 분모는 cluster $k$로 분류가 되는 data point의 colleted portion이 되고, 분모는 cluster $k$와 관련된 data point의 wieghted sum이 된다.

이러한 방식이 괜찮아보일 수 있다. 그러나 누군가는 soft K-means을 만드는 과정에서 의문을 가질 것이다. 왜 각 vector $r_{ki}$에 대해서 softmax를 이용하는 것일까? 왜 centroid는 저렇게 만들어야 할까?

Interpretation of Soft K-means

이러한 것을 이해하기 위해서 corresponding joint optimization problem에 대해서 알아보려고 한다.

우리가 원하는 것은 원래의 K-means와 같은 cost function을 최소화하는 것이다. Data point와 centroid간 distance의 weighted sum을 최소화하고 싶은 것이다. 여기에 soft K-means는 smooth $r_{ik}$를 가지기 위해서 추가적인 cost를 추가로 사용한다. 그래서 두번째 항은 각 assignment에 대한 entropy의 sum으로 이해될 수 있고, entropy를 작게 하기 위해서 두번째 항을 추가적으로 고려한 것이다.

$\beta$는 control knob으로 clustering의 simplicity와 reference points의 representability 사이의 trade-off이다. 여기서 $\beta$는 작아지기를 원하고, 작아지게 되면 soft assignment를 나타내게 된다. 만약 $\beta$가 무한대라면, soft K-means가 원래의 K-means와 같아지게 된다. 이것이 soft K-means를 해석하는 방법이다.

Finite Mixture Model

Machine learning을 연구할 때 K-means나 soft K-means보다도 더 직관적인 방법이 필요하다고 생각한다. Gaussian mixture model(GMM)이 그 중 하나가 될 수 있는데, 만약 GMM을 가정하고 algorithm을 만든다면 soft K-means algorithm과 똑같이 할 수 있다. 이는 soft K-means를 사용하면 GMM과 매우 유사한 특정 data 형태를 가정한다는 것을 의미한다. 그러면 이제 GMM의 정의로부터 시작해보고자 한다. 그 전에 mixture model에 대해서 먼저 알고 가야한다.

Finite mixture model은 data point를 여러 개의 distribution category로 이루어졌다고 가정하는 것이다. 더 구체적으로 likelihood가 여러 distribution의 weighted sum으로 분해된다. Likelihood를 분해한다는 것은 data point의 generation을 가정하겠다는 것이다. 먼저 vector로 주어진 $p(z=k)$에 따라 각 data point의 class나 cluster index를 결정할 것이다. 그리고 이 data point의 assignment가 주어지면 우리는 해당 class나 cluster에 의존하는 distribution $p_k$로부터 data point를 만들 것이다. $p(z=k)$는 어느 cluster에 속하는지에 관한 probability로 일종의 prior이고, $p_k(x)$는 해당 cluster에서의 probability로 일종의 likelihood가 된다. 편리함을 위해서 assignment에 대한 marginal distribution인 $p(z=k)$를 mixing parameter $\pi_k$로 나타낼 것이고, 각 cluster $k$에 포함 될 확률들을 나타내므로 전체 $\pi_k$의 합은 1이 된다.

Gaussian Mixture Model: Graphical Representation

우리는 각 cluster distribution을 Gaussian distribution으로 가정할 것이다. 그러면 GMM을 정의할 수 있다. 더 나은 이해를 위해서 $x_i$의 generation을 설명할 것이다. 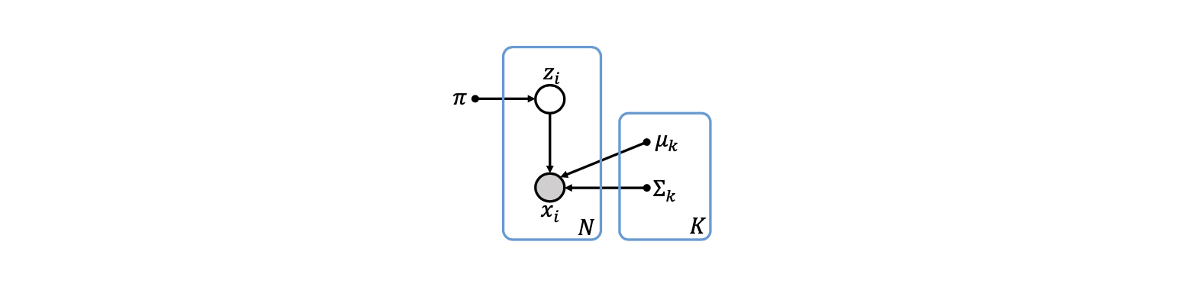Mixing parameter $\pi$에 따라서 우리는 data point의 true assignment $z_i$를 결정할 것이다. 이를 기반으로 평균이 $\mu_{z_i}$이고 표준 편차가 $\Sigma_{z_i}$인 Guassian distribution의 data point를 그릴 것이다. 이 generation은 위와 같이 grph로 나타낼 수 있으며, 더 형식적으로 $z_i$의 marginal probability를 $\pi_k$의 곱으로 나타낼 수 있다.

그리고 $z_i$가 주어졌을 때 conditional distribution은 다음과 같이 정의할 수 있다.

만약 $z_i=l$이라고 미리 주어지면 $\pi_k$의 distribution은 $\mathcal{N}(x_i|\mu_l,\Sigma_l)$와 같아진다.

Gaussian Mixture Models: Intuition

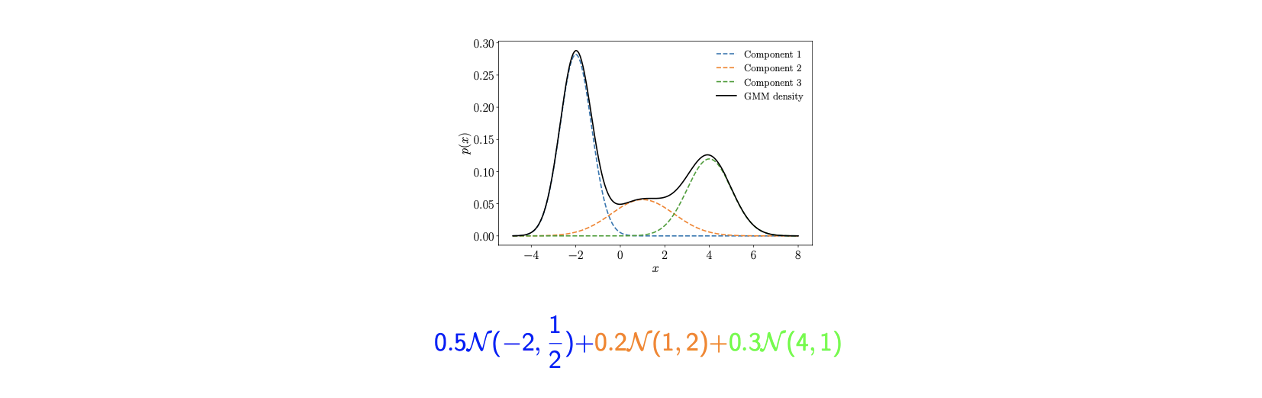GMM의 예시로 3개의 cluster가 있고, 각각의 cluster가 위와 같은 Gaussian distribution이라면, 각 cluster의 distribution $p_k$는 위와 같이 cluster의 weighted sum으로 $x$의 marginal distribution과 같다. Mixing parameter $\pi_k$는 각 cluster의 distribution에 속하게 될 probability로 위에서는 0.5, 0.2, 0.3으로 나누어졌다.

Clustering을 연구하는 것이 정말로 타당한 이유는 input dimension이 주어졌을 때 clusted component처럼 보이는 어떠한 data distribution을 기대할 수 있다. GMM은 각 cluster에 Gaussian distribution을 부여하는 것이 가능하다.

Learning GMM

GMM을 학습하는 것은 모든 parameter에 대해서 miximg parameter $\pi_k$와 각 parameter $\mu_k, \Sigma_k$를 최적화 함에 따라서 다음과 같은 probability $r_{ik}$을 추출하는 clustering을 나타낸다.

Parameter Estimation via MLE

그래서 $\pi_k,\mu_k,\Sigma_k,r_{ik}$를 얻기 위해서 MLE와 같은 parameter estimation 방식으로 접근할 수 있다. 이를 위해서 i.i.d. 가정을 하고 시작할 것이다. 그러면 dataset의 likelihood는 다음과 같이 적을 수 있다. 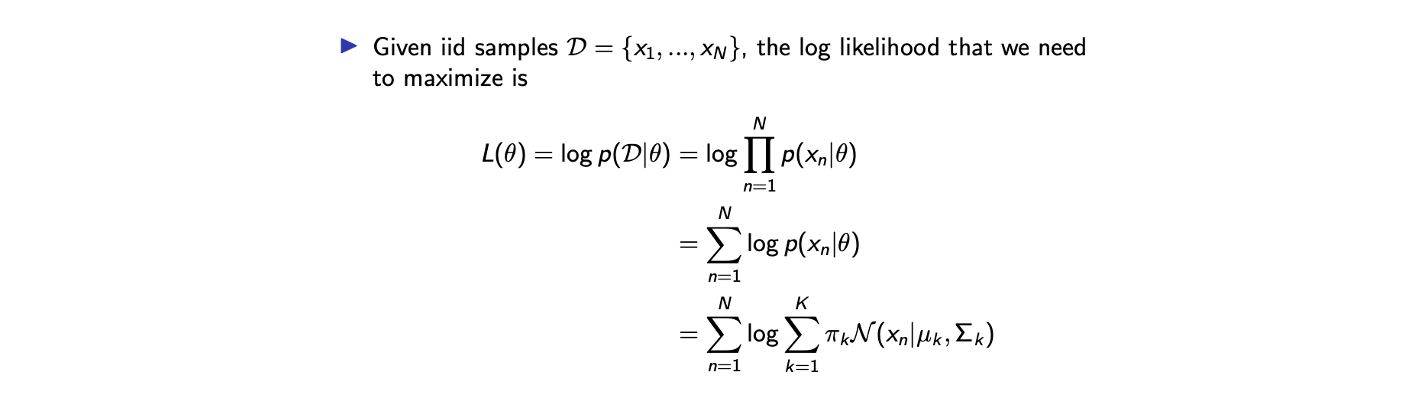우리가 원하는 것은 위의 log-likelihood를 최대로 하는 parameter $\theta$를 얻는 것이다.

There is No Closed-Form Solution

그러나 아쉽게도 이 optimization problem에서 closed-form solution이 존재하지 않는다. 왜냐하면 log-likelihood는 convexity나 concavitiy가 없기 때문이다. 그래서 이렇게 수학적으로 다루기 어려운 문제를 피하기 위해서 우리는 expectation-maximization(EM) algorithm을 적용할 것이다.
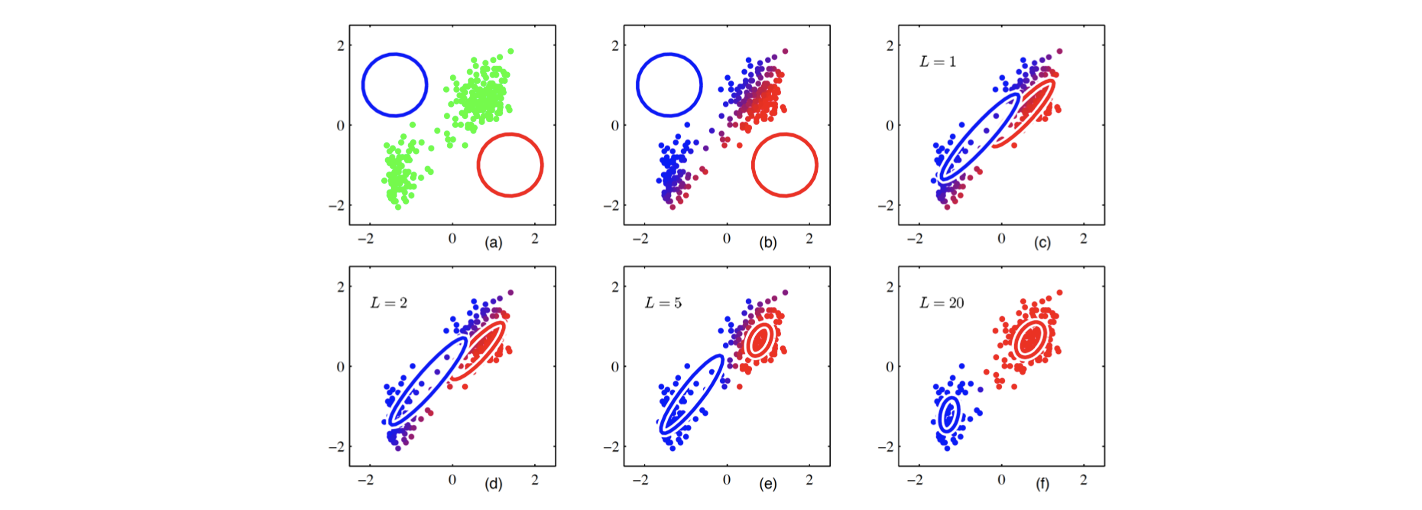시작은 parameter $(\pi_k,(\mu_k,\Sigma_k))$의 initialization으로부터 할 것이다. 그리고 이로부터 $r_{ik}$를 할당할 것이다. 그래서 $r_{ik}$를 기반으로 다시 $\pi_k,\mu_k,\Sigma_k$를 업데이트 할 것이다. 이러한 과정을 반복해서 진행하면 위에서는 20번의 반복 후에 모든 parameter와 clustering을 찾을 수 있다.

Example: EM for Isotropic GMM

GMM에 대한 EM algorithm의 형식적인 정의는 다음과 같다. 편리함을 위해서 isotropic GMM을 정의할 것이다. 이는 GMM에 하나의 constraint를 추가한 것 뿐이다. Isotropic GMM은 covariance matrix에서 diagonal entry를 제외하고 전부 0인 경우를 말한다. $\theta$는 $K$개의 tuple로, 각 tuple은 $\pi_k,\mu_k,\Sigma_k$를 가지고 있다. 그래서 총 $3K$개의 variable을 가지게 된다. 그리고 complete-data가 의미하는 것은 likelihood를 $x_i$ 뿐만 아니라 $z_i$ 까지 사용하겠다는 것이다.
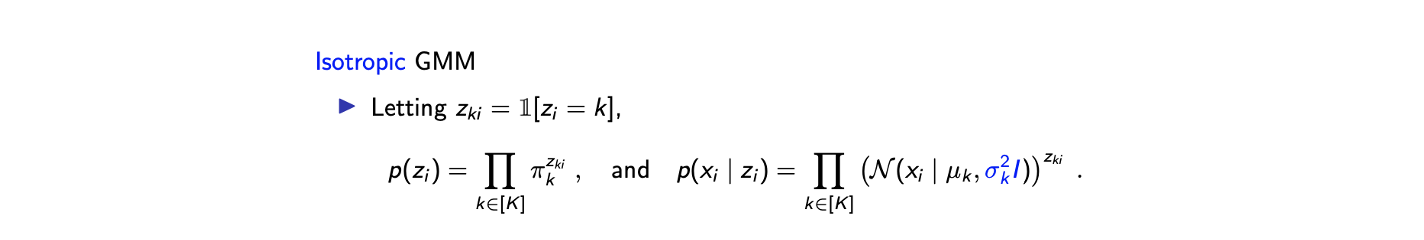이렇게 표준편차를 정의하면 parameter의 개수를 줄일 수 있다. $p(z_i)$와 $p(x_i|z_i)$ 항을 곱해준다면 joint distribution $p(x_i,z_i)$가 된다.

Log-Likelihood for GMM

EM algorithm을 만들기 위해서 먼저 log-likelihood로 쓰여진 complete-data $L_c$ 가 다음과 같이 필요하다.
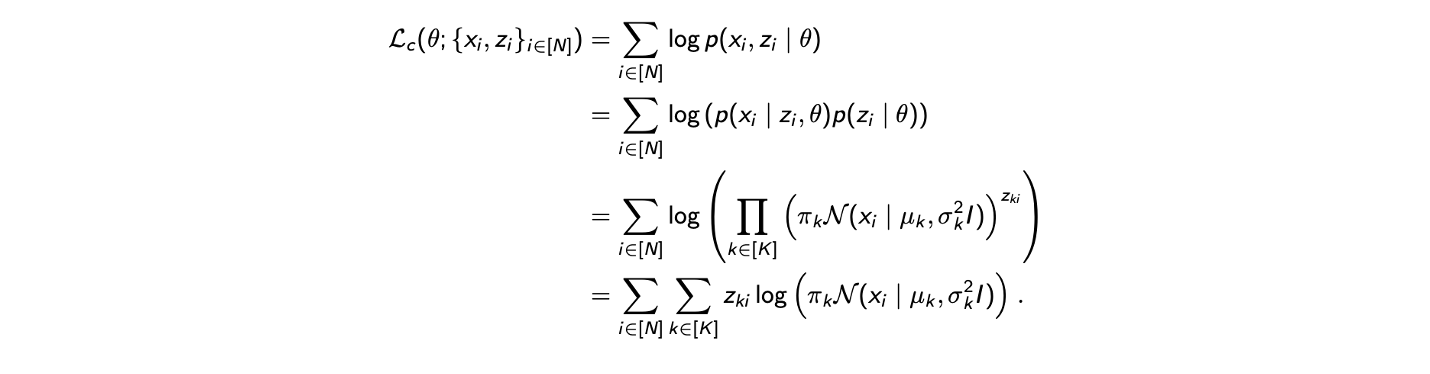첫번째 등호는 정의로부터 나온 것이고, 두번째 등호는 Bayes rule에 의해서 바뀌었다. Complete log-likelihood data는 원래 log-likelihood의 lower bound를 근사한 것이다. 그리고 isotropic GMM의 가정으로부터 complete log-likelihood data를 위와 같이 정의할 수 있다. 아쉽게도 마지막 등호와 같은 식을 최적화 하기는 어렵다. 이를 계산하기 위해서는 무언가 더 필요하다. 왜냐하면 $z_{ki}$ 가 latent random variable이고 우리가 최적화 하고 싶은 것은 4개의 parameter들이다. 이는 우리가 parameter $\theta$에 관한 complete log-likelihood를 최적화 하기 위해서는 $z_i$를 다뤄야 한다는 것이다. 그래서 이를 근사하는 방법 중 하나는 complete log-likelihood의 expecation을 취하는 것이다.

추가적으로 parameter $\theta'$ 가 주어졌을 때, $z_{ki}$를 알고 있고 expectaion을 사용할 수 있다. 우리는 actual log-likelihood를 complete log-likelihood의 expecation으로 근사할 수 있다. Comeplete log-likelihood data는 다음의 conditional expectation $Q$ 처럼 다시 나타낼 수 있다. Notation의 편리성을 위해서 $Q(\theta;\theta')$을 $\theta'$으로부터의 $z_i$에 관한 expectation으로 정의할 수 있다. 그러면 이 complete log-likelihood는 이전의 계산으로부터 두번째 등호와 같이 주어지게 될 것이다. 그리고 $r_i$를 정의했기 때문에 세번째 등호와 같이 바꿀 수 있다. 마지막 등호는 Gaussian distribution의 정의로부터 정리할 수 있다.

EM for GMM

그러면 이제 GMM에 대한 EM algorithm은 마지막 등호를 2-step을 통해서 최적화 하는 것이다. E-step에서는 $\mathcal{Q}$를 최대로 만드는 $r_{ik}$를 계산한다. 그리고 M-step에서는 $\mathcal{Q}$를 최대로 만드는 $\theta$를 업데이트한다. 이는 간단한 아이디어이고 M-step을 자세히 보고자 한다.

M-step: Gaussian Parameters

M-step은 derivative를 구해서 0으로 두고 풀게 된다. 그 결과 mean과 variance parameter는 다음의 식을 통해서 얻을 수 있다.

$\text{Mean: }$

$\text{Variacne: }$

편의성을 위해서 $\sigma^2$ 에 관해서 미분을 해주는 것이다.

M-step: Mixing Parameters

남은 parameter는 $\pi_k$이고, 다음과 같이 구할 수 있다. 이는 추가적으로 non-trivial optimization을 필요로 한다. $\pi_k$의 합은 1이어야만 하고, 이는 $\pi_k$를 구하기 위해서 우리는 constraint optimization problem을 풀어야 한다. 이는 Lagrangian method를 이용해서 구할 수 있다.

Em Algorithm for Isotropic GMM: Summary

EM algorithm의 insight를 알기 위해서 $\mu_k$를 $x_i$의 weighted averge인 centroid로 생각할 수 있다. 그래서 assignment의 몫은 $r_{ik}$에 의해서 주어지기에 $\mu_k$는 cluster $k$에 속하는 $x_i$의 weighted sum을 cluster $k$에 대한 assignment의 sum으로 나눈 것이다. 그래서 이를 centroid라 생각하는 것이고, 이와 비슷하게 $\sigma^2$는 variance인데 empirical estimation variance라 생각하면 된다. 분모는 cluster $k$에 대한 weighed sum이고 분자는 data point와 새로운 centroid간 squared error, 혹은 distance의 weighted sum이다. 마지막으로 mixing parameter $\pi_k$는 data point $N$개에 대해서 cluster $k$에 대한 assignment의 합이다.

K-means: Special Case of EM for GMM?

만약 모든 cluster $k$에 대해서 mixing parameter $\pi_k$를 $\frac{1}{K}$로, $\sigma_k^2$를 $\sigma^2$으로 같게 선택한고 $\sigma^2$가 0으로 간다고 했을 때, EM algorithm은 K-means algorithm과 같아질 것이다. K-means algorithm을 사용하는 것은 각 cluster에서 동일한 mixing parameter와 variance를 가진 GMM을 가정하는 것이다.