[기계학습] Generative Model - Generative Adversarial Network(GAN)

GAN은 VAE와 더불어 generative model의 또 다른 예시로서, image나 data를 만들어내는 유망한 방법 중 하나이다.

Focus on Generation

VAE를 training하는 것은 non-trivial summation을 필요로 하고, 때때로 엄청난 계산을 요구하게 된다. 성능은 다소 괜찮지만 충분하지 못하다. 그래서 우리는 non-trivial summation을 피하고자 하고, 여기서 이러한 계산은 likelihood의 explicit한 계산으로부터 생기게 된다. 그래서 likelihood를 계산하는데 latent space에 대한 non-trivial summation을 필요로하게 된다. 이러한 부분을 피하고자 사용하는 방법 중 하나가 GAN이다. GAN은 Gaussian noise와 같이 간단한 distribution부터 training sample distiribution까지의 transformation을 학습하는데 초점을 맞추고 있다. 이러한 insight는 VAE의 insighte와 비슷하다. 그러나 GAN은 encoder-decoder 구조와 같은 것을 사용하기 보다는 바로 latent code $z$를 $x$로 변환하는 것을 시도한다.

Training GAN: Two-player Game

GAN의 architeture는 다음과 같다.
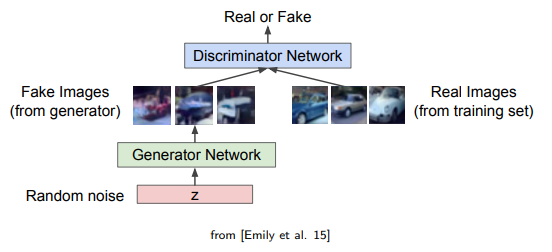GAN은 generator network(G)와 discriminator network(D)로 구성되어 있다. GAN에서 N은 networks를 의미하며 이는 2개의 network를 사용한다는 의미이다. G는 진짜같아 보이는 fake image를 만들어서 D를 속이려고 하는 반면 D는 G가 만들어낸 fake image와 real image를 구분하려고 한다. 결국 이러한 구조로부터 우리가 바라는 것은 2개의 player가 반복해서 그들의 능력을 발전시키고 결과적으로 훌륭한 fake image를 만들어내도록 하는 것이다. 그래서 이를 two-player game이라 부르게 된 것이다.

형식적으로 GAN에서 two-player game이라 하는 것은 G와 D 사이의 경쟁이고 다음과 같이 나타낼 수 있다. 그리고 여기서 D를 binary classifier라고 생각하면서 real image(1)과 fake image(0)을 구분하고자 할 것이다. 그래서 이를 기반으로 다음과 같이 minimax optimization problem으로 정의할 수 있다.

min은 G에 대응하면서 parameter $\theta$를 가지고, max는 D에 대응하면서 parameter $\phi$를 가진다. 그러면 objective를 이해하는데 다소 어려움이 없을 것이다.

먼저, binary classifier로서 D에 대해서 자세히 보도록 하자. 여기에는 2개의 dataset이 필요하며, 하나는 만들어진 가짜들이고 나머지는 주어지는 진짜들이다. 위의 식에서 첫번째 expectation term은 real data distribution에 관해서 계산되고 두번째 expectation term은 generative model로부터 계산된다. 그러면 D는 real data에 대해서 1 또는 x의 답을 목표로 한다. 그래서 첫번째 expecation term을 최대로 하려고 하는 것이고, 두번째 expectation term은 latent code G에 대해서 계산되어 G로부터 fake data를 만들어내게 된다. 그래서 두번째 expectation을 $E_{\hat{x}\sim p_{G_\theta}}[\dots]$처럼 똑같이 나타낼 수 있고, 기존의 $G_\theta(z)$가 $\hat{x}$으로 대체될 수 있다. 그래서 maximization에서 D에 대한 두번째 term은 G로부터의 data가 fake이기 때문에 0이 되도록 분류하는 것을 목표로 한다. 결론적으로 D를 다음과 같이 해석할 수가 있는 것이다.
이번에 반대로 G는 D를 속이고 싶어해서 D의 objective function을 최소로 만들고 싶어한다. 그래서 $\theta$에 대한 minimization이 $\phi$에 대한 maximization 앞에 등장하게 된다. Objective function에서 첫번째 term은 generative model에 의존하지 않기 때문에 G는 오로지 두번째 term을 최소로 만들고자 한다.

구체적으로 GAN에 대한 코드를 작성해야 한다면 이 minimax problem을 2개의 optimization으로 풀어나가야 한다. 하나는 discriminator에 관한 것이고, 다른 하나는 generator에 관한 것이다. Discriminator는 다음 2개의 term을 최대로 만들고자 하고, generator는 첫번째 term과는 independent해서 마지막 term만을 최소로 만들고자 한다.

$\text{Gradiant ascent on discriminator: }$

$\text{Gradiant descent on generator: }$

이론적으로 진짜와 가짜를 잘 구별하는 discriminator와 discriminator를 잘 속일 수 있는 generator를 가지는 것이 가능해야 한다. 아쉽게도 이러한 이론적인 framework는 몇가지 문제점 때문에 현실에서 잘 동작하지 않게 된다. 그 중 하나가 generator의 objective function에 있다.

Heuristic to Improve Convergence

상대적으로 discriminator와 비교했을 때 generator가 좋지 못한 상태라고 가정해보자. 이러한 경우에 generative model의 optimization에서 gradient가 거의 0이 된다. 즉, G가 D와 비교해서 좋지 못하다면, discriminator는 generative model로부터 모든 fake image를 구분할 수 있게 된다. 이는 $D(G(z))$가 0에 근사함을 의미하게 된다. 이렇게 되면 이러한 지점인 $\text{log }(1-D)$에서의 gradient가 거의 0에 수렴하게 된다. 수치적으로 gradient 값이 너무 작아서 generator가 개선할 여지가 존재하지 않게 된다. 그래서 이러한 문제를 피하고자 heuristic한 해결법을 제안했다. 그 방법은 기존의 logarithm을 negative로 바꾸는 것이었다.

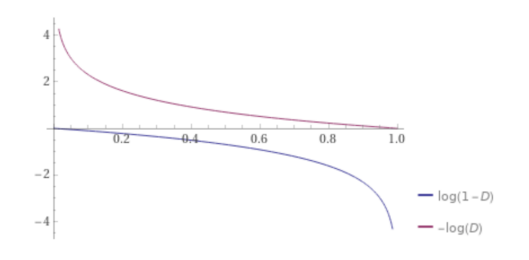이렇게 식을 바꿈으로서 D가 0에 가까울수록 더이상 gradient 값이 0에 수렴하지 않게 된다. 이렇게 하면 generative model이 업데이트 할 수 있는 기회가 제공이 되고 GAN의 convergence가 개선될 수 있다. 이렇게 식을 바꾸는 것은 어느정도 trade-off로 보일 수 있다. D가 0에 가까워질수록 기존의 식의 gradient가 0에 수렴되게 되지만 D가 1에 가까워지면 반대로 gradient가 커졌었다. 반면, negative logarithm을 사용하게 되면 D가 0에 가까워지면서 큰 값의 gradient를 가지게 되고 D가 1에 가까워지면 이번에는 반대로 gradient가 0에 수렴하게 된다.

위의 그래프에서 D가 1에 가까워져서 0에 수렴한 경우가 generative model에 있어서 가장 좋은 상황이다. 이렇게 되면 generator가 더이상 업데이트가 될 필요가 없게 된다. 이러한 의미에서 식을 변형해서 사용하는 것이 heuristic하게 받아들일 수 있는 상황이 되는 것이다. Discriminator를 업데이트하면서 특정 구간에서 generator를 업데이트 시켜주게 된다. 이러한 과정은 generator가 좋아지는 특정 지점에 수렴할 때까지 반복하게 된다.

Generating Data from GAN

GAN을 학습시키고 난 후에 generator 부분을 사용해서 data를 만들어내게 된다.
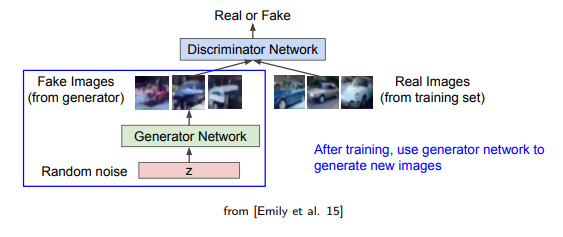다음은 GAN을 사용해서 image를 만들어내는 예시들이다.
위의 예시를 보면 가장 우측에 배치된 image들이 real data에 해당하고, 나머지 부분이 GAN에 의해 학습이 된 generative model이 만든 output에 해당하게 된다. 결과들을 보면 꽤 그럴듯한 것을 확인할 수 있다.

위는 DCGAN을 사용한 예시이고 이는 GAN의 부족한 부분을 보완하기 위해서 등장했다.

이번에는 StackGAN으로 기존의 GAN을 보완하고자 새로 등장한 method들이 다양하게 존재한다.

Known Issues with GAN

기존의 GAN이 그럴듯한 결과를 만든다고 하더라도 몇가지 해결해야 할 문제들이 있다. GAN의 convegence에 있어서 문제를 일으키는 2가지 issue가 존재한다. 하나는 non-convergence issue이고, 다른 하나는 mode-collapse issue이다.

Non-Convergence

Minimax problem에서 non-convergence는 근본적인 문제이기도 하다. 이를 다음의 예시를 통해서 보도록 하자. 우리는 minimax objective function이 다음과 같다고 가정할 것이다.

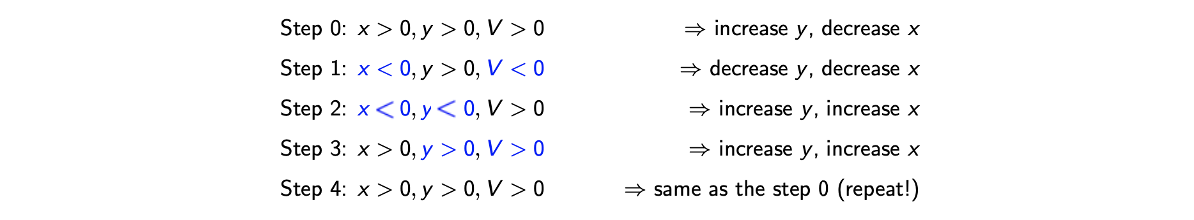
2개의 variable에 대해서 optimization을 해야하는 상황이며 obejctive function은 2개의 variable의 곱으로 나타낸 것이다. 가장 먼저 $x,y$를 양수로 초기화한다고 하면, 이러한 variable의 선택으로 인하여 local optimization 과정에서 $y$는 증가시키고 $x$는 감소시킬 것이다. $x$는 $y$가 양수이기에 이 gradient는 양수가 되어 obejctive를 최소로 만들기 위해서 감소해야 한다. 이러한 흐름으로 $y$의 상황을 봤을 때 $y$는 증가해야 한다. 이렇게 local optimization에서 한 과정이 진행되었다. 다음 단계에서 $x$가 음수이고 $y$가 양수인 상태라면 $V$는 음수가 될텐데, 이러한 경우에 또 다른 descent gradient step에서 $y$와 $x$ 모두 감소시키는 결정을 할 것이다.

이러한 local optimization을 여러 단계 하다보면 objective value의 부호가 동일하게 반복되는 것을 볼 수 있어서 minimax optimization이 원활히 이뤄지지 못하게 된다. Learning rate의 크기를 작게 한다고 하더라도 이 optimization이 수렴하지 않는 문제가 된다. 이렇게 완전히 같은 상황이 GAN을 학습시키는 동안 매번 발생하지는 않지만 이러한 상황이 종종 발생해서 문제가 되곤 한다. 그래서 GAN의 convergence를 볼 수 있다는 사실은 기적과도 같은 것이다.

Mode-Collapse

다음으로 잘 알려진 issue로는 mode-collapse가 있다. 사실 이 mode-collapse 문제는 다른 논문들에서 잘 해결이 된 사실이지만 GAN의 학습에 있어서 유명한 issue였다. 특정한 소수의 data class에만 괜찮은 결과를 generator가 생성함으로써 discriminator를 속일 수 있다. 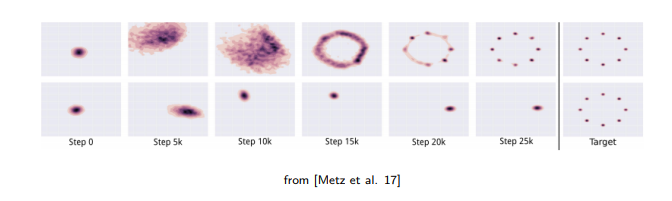예를 들어 8개의 class를 가지고 있고 clustering이 잘되었다고 가정해보자. 이러한 경우에 generator가 생성해야하는 것은 예상하게 된다면 8개의 cluster일 것이다. 하나의 cluster를 골라서 이 cluster에 속하는 data를 생성해서 discriminator를 속이는 것도 가능하다. 왜냐하면 이것 조차도 real data와 정확하게 일치하기 때문이다. 그래서 dsicriminator를 하나의 cluster에 속하는 data만을 만들었다고 할지라도 이것이 원래의 real data와 정확하게 일치하기 때문에 틀렸다고 말할 수 없는 것이다. 이러한 이슈를 mode-collapse라고 하며, 실제로 이러한 현상이 자주 일어나게 된다.

Simple Trick to Avoid Mode-Collapse: Mini-Batch GAN

Mode-collapse 문제를 피하고자 mini-batch GAN이 등장하였다. Mini-batch GAN은 generative model에게 다양성을 강제할 수 있다. Generative model이 sample들의 mini batch를 만들어서 해당 batch에서 다양성을 조절하도록 하면 된다. 만약에 generative model이 매우 유사한 sample들을 가지고 있다면 generative는 불이익을 받게 될 것이다.

다양성을 지키는 방법 중 하나로 만들어진 fake image의 feature distance를 측정하는 L2 norm을 사용할 수 있다. 이렇게 하면 다양한 batch를 만들 수 있고 결국에는 mode-collapse 문제를 막을 수 있다. Mode-collapse 문제를 해결하는 방법에는 이 외에도 다양하게 존재한다.

Revisit GAN Objective

지금까지 GAN이 어떻게 동작하고 학습하는지 대략적으로 이해해왔다면 이번에는 GAN에 대해서 좀 더 자세하게 분석해보도록 할 것이다. Generative model, generator가 주어졌을 때마다 optimal discriminator를 가지고 있다고 가정할 것이고, 여기서 optimal discriminator $D_\phi(x)$를 분석해보자. Generator에 대한 obejctive는 다음과 같다.

편의성을 위해서 2번째 term을 기존의 Gaussian prior에서 $x$에 대한 generative model로 대체하였다. 이렇게 식을 대체해서 사용하는 것이 가능한 부분이고, 이 obejctive가 주어지게 되면 optimal discriminator에 대한 설명을 단순화할 수 있다.

첫번째 등호는 objective 식을 자세하게 풀어 적은 것으로, derivative를 구하고 0으로 놓게 되면 알아낼 수 있다.

그리고 두번째 등호는 $p_{data}, p_G$ 사이의 JS divergence의 2배를 한 식에 constant를 빼주는 식으로 바꿀 수 있다. 이는 generator의 objective가 분포 간 어떠한 측정으로 대체될 수 있다는 것을 의미한다. JS divergence는 서로 다른 두 분포 간의 불일치를 측정합니다. 이러한 내용을 기반으로 GAN의 framework를 더 일반적인 objective function과 divergence measure로 일반화할 수 있다.

f-Divergence

f-divergence는 JS divergence의 일환으로 2개의 분포 간 거리를 측정하는데 사용이 된다.

여기서 $f$는 임의의 convex, lower-semicontinuous function이고 $f(1)=0$가 된다. $p,q$의 차이는 더 큰 divergence를 설명하고 0 divergence는 $p,q$가 일치한다는 것을 의미한다. 이러한 것들은 $f$가 convex라는 것으로부터 보장받을 수 있다. 하나의 예시가 JS divergence, 혹은 KL divergence이다. 이렇게 GAN은 어떠한 f-divergence objective function으로 수식화 될 수 있다. 이러한 부분이 GAN을 일반화시킬 수 있다. 다음은 잘 알려진 GAN에서의 divergence의 여러 선택지들이다.