[기계학습] Graphical Model - Construction of Graph from Data

이제 우리가 해결하고자 하는 남은 문제는 data로부터 어떻게 graphical model을 구성하는지이다. 지금까지는 graphical model이 주어진 상황에 대해서 생각해왔다. 그리고 이로부터 algorithm을 build하고 conditional independence를 확인하는 등 여러가지를 했었다. 그러나 때때로 그러한 statistical model을 graphcial model로서 정의하는 것은 어렵다. 그래서 누군가가 graphical model을 data로부터 구성하는 reverse problem에 대해서 생각해냈다. 이번 내용에서는 강력하고 전통적인 Chow-Liu algorithm(1968)에 대해서 알아보려고 한다. 이 algorithm은 acyclic graph를 만드는 방법을 제시했고, 여기서 BP algorithm이 exact함을 보여줬다.

Learning Graph Structure from Data

어떻게 하면 data로부터 graph를 만들 수 있을까? 모든 graph는 이웃하는 variable의 correlation을 나타내는 edge와 variable들로 구성되어 있기 때문에 variable 사이의 correlation을 통해서 graph를 build 할 수 있다. 그래서 Chow-Liu algorithm도 이러한 식으로 pair-wise corrleation을 통해서 graph를 만들려고 했다.

본격적으로 총 $K$개의 sample들로부터 $N$개의 random variable로 계산된 joint probability의 empirical distribution $p$로부터 시작해보자.

Empirical joint distribution은 어떠한 random varable의 configuration에 대한 probability가 dataset에 있는 해당하는 configuration의 frequency 혹은 ratio와 같아지게 되고, 형식적으로 다음과 같이 나타낼 수 있다.

Dataset $\mathcal{D}$에 있는 각각의 sample들은 $N$ 차원의 data이라서, 위와 같이 empirical distribution을 정의할 수 있게 된다. 우리는 특정한 configuration $x$를 관찰하는 횟수를 셀 수 있고, 이를 sample의 전체 개수인 $K$로 나눌 수 있다. 이러한 joint distribution을 그 자체로 사용할 수 있지만, 일반적으로 매우 많은 수의 variable을 사용하기 때문에 binary인 경우만 해도 $2^N$의 sample들을 다뤄야 한다. 이는 sample의 개수은 $K$보다 월등히 크기 때문에 우리는 approximation을 통해서 구할 필요가 있다. 우리는 graph를 만들기 위해서는 아직 관찰이 되어지지 않은 것까지 예측할 필요가 있다. 이에 대해서는 뒤에 더 자세하게 보도록 할 것이다.

이러한 joint distribution의 크기는 너무나도 크기 때문에 다루기가 너무 힘들 것이다. 그래서 computational effieciency적인 측면에서 매우 도움이 되는 간단한 graphical model이나 factorized joint distribution을 build하기를 원한다.

A Simple Structure: Directed Tree

간단한 구조를 만들기 위해서 우리는 directed tree에 대해서 다뤄보려고 한다. Tree라는 구조를 사용하려는 이유는 tree라는 것 자체가 BP의 exactness를 보장하고 동시에 edge의 수가 tree인 경우에는 최대 $N-1$개이기 때문이다. $N-1$개의 edge인 이유는 graph 상에 cycle이 존재하지 않기 때문에 만약 모두 connected 되어 있다면, edge의 수는 node의 수에서 1을 뺀 값이 된어 tree에서의 edge의 수는 $N-1$보다 작거나 같게 bound가 된다.

Chow-Liu algorithm은 주어진 empirical joint distribution에 대한 directed tree를 만드는데 초점을 두고 있다. 그리고 Chow-Liu alogrorithm은 second-order distribution에 초점을 맞추고 있다. 여기서 second-order라는 것은 factorized joint distribution을 가지게 될 것이라는 것이고, joint probability $p(x_1,x_2,x_3,x_4,x_5,x_6)$를 다음과 같이 $p(x_i|p_{\partial{i}})$항들의 조합으로 만들 수 있다.

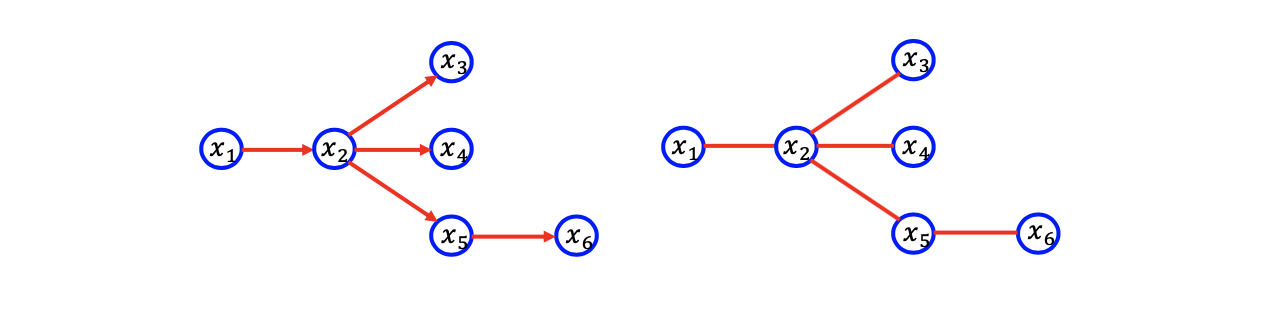여기서는 head-to-head topology는 존재하지 않는다. 여기서 parent의 수는 1이 되고, 이러한 것이 추가 제약 조건이다. 그러나 이는 directed graphical model에서 random variable간 correlation을 단순화 할 것이다. 그래서 이러한 부분에 초점을 맞춰서 생각해보도록 할 것이다.

또한 directed graphcial model에서 이러한 limitation들을 가지게 된다면 위와 같은 좌측의 directed graphical model은 edge에 대해서 각각의 potential function이 예를 들어 $p(x_2\x_1)$과 같은 식으로 대응되는 undirected graphcial model로 바뀔 수가 있다.

Problem Formulation

Chow-Liua algorithm을 설명하기 위해서 먼저 problem formulation을 알아두고 갈 필요가 있다. Problem formulation은 tree graph를 만드는 목표인 state이다. 목표를 선택하는데 있어 가장 자연스러운 방법은 empirical distribution $p$와 approximated distribution $p_T$ 사이의distance를 최소화하는 것이다. 여기서 $T$는 tree를 의미한다.

우리는 이러한 distribution간 차이를 최소화하고 싶고, 이는 곧 이 문제에 대한 자연스러운 목표가 될 것이다. 이 차이는 KL divergence 식으로 나타낼 수 있다. 물론 이러한 방법말고 다른 방법을 사용해서 distribution간 차이를 줄일 수 있다. 그러나 KL divergence는 가장 자연스러운 선택이 될 수 있고, distribution간 차이를 설명하는데 있어 가장 유명한 선택이 될 것이다. 대칭성 때문에 KL divergence를 반대로 적용해도 상관이 없다. 그래도 우리가 순서를 $KL(p\|p_T)$로 사용하는 이유는 $p$가 표준이 되기 때문이다. 우리는 $p_T$대신에 $p$를 보게 된다. 그래서 우리는 empirical error를 최소화하기 원하게 된다. 이를 위해서 순서를 이렇게 해서 KL divergence를 고려할 필요가 있게 된 것이다. 만약 우리가 reverse $KL(p_T\|p)$를 고려한다면, absolute continuous를 보장할 수 없어서 KL divergence가 정의되지 않을 것이다. 만약 $p_T(x)>0$이고 $p(x)=0$ 이라면 $KL(p_T\|p)$의 정의되지 않아서, 우리는 이러한 상황은 피해야 한다. 그래서 결국 $KL(p\|p_T)$를 사용하게 되는 것이다.

이제 위에서 살펴 본 제약 조건을 통해서 우리는 KL divergence를 최소화 하고 싶다. $p_T$는 Bayesian network T에 대응하는 distribution으로 다음과 같이 정의할 수 있다.

Factorization in Directed Tree

Directed tree graph에는 제약 조건이 존재하기 때문에 우리는 $p_T$를 다음과 같이 더 단순화 할 수 있다.
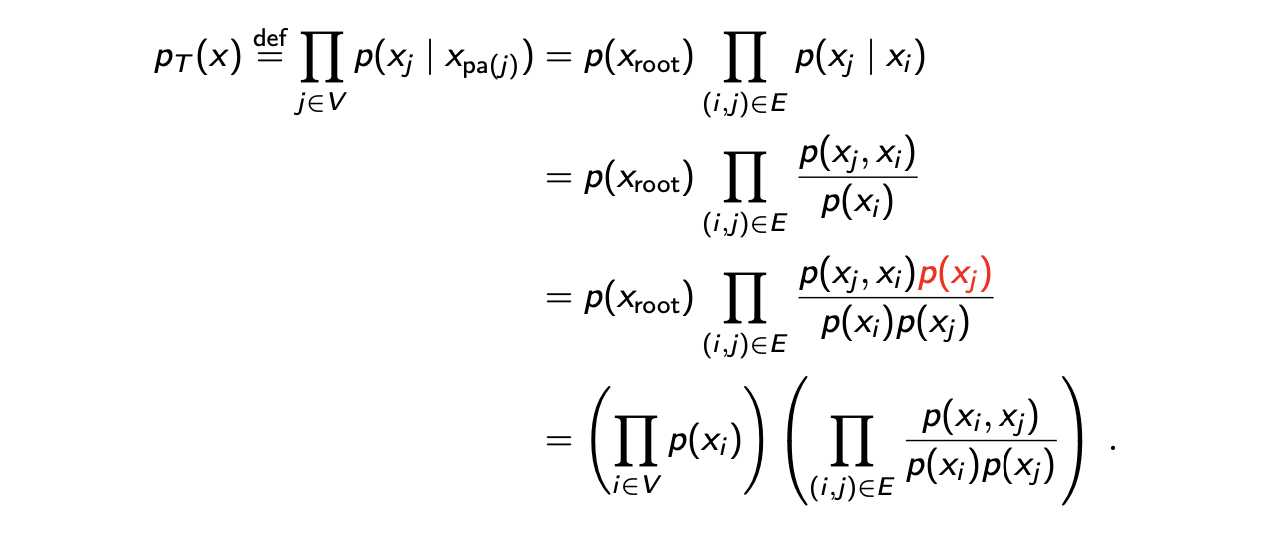정의에 의해서 우리는 approximated joint distribution이 factorized 되는 것을 알 수 있고, 이는 다시 root node의 marginal probability와 각각의 edge의 marginal conditional probability이 곱해진 형태가 된다. Conditional probability의 정의에 의해서 다시 식이 joint probability와 marginal probability로 바뀌고, $x_j$의 marginal probability를 분자, 분모에 곱해줌으로써 우리는 approximated joint probability를 모든 variable에 대한 marginal probability의 곱과 모든 edge의 2개의 variable의 joint probability를 각각의 marginal probability로 나눈 항의 곱으로 다시 적어서 단순화 할 수 있다.

Finding The Best Approximation

이로부터 오직 marginal probability와 pair-wise joint probability를 필요로 하게 되는 $p_T$를 계산하는 효율적인 algorithm을 생각할 수 있다. 우리가 하려는 것은 KL divergence를 최소화하는 것이었다.
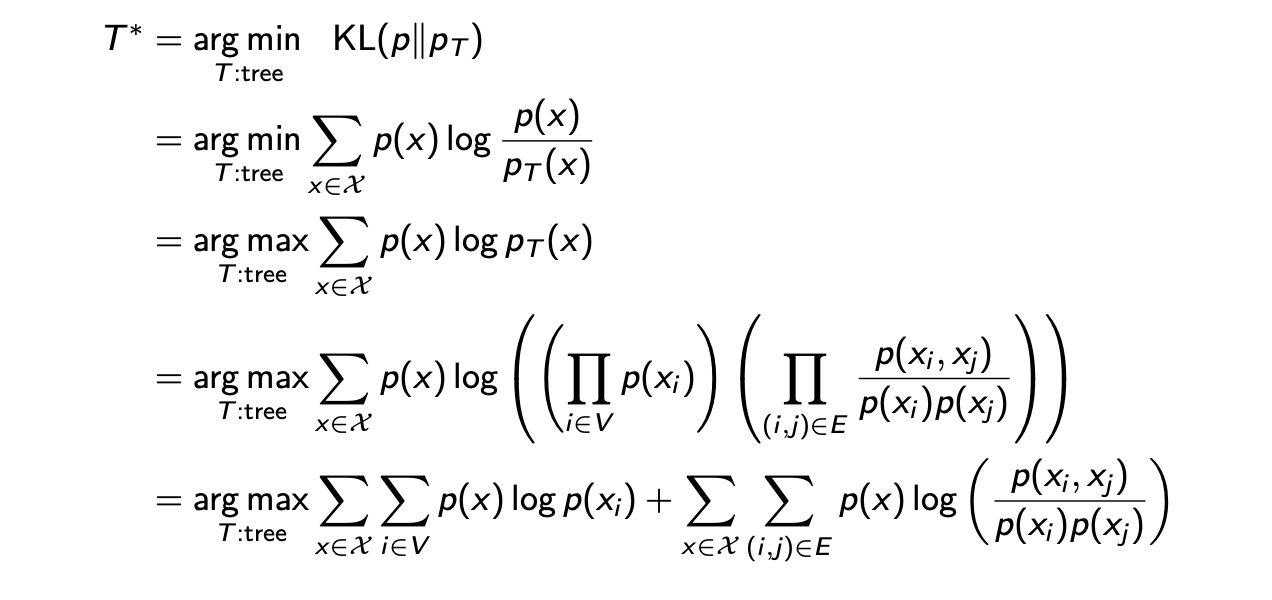먼저 이전의 KL divergence를 계산한 식을 대입하고 $p_T$를 최대화하는 식으로 바꿔서 $p_T$에 위에서 단순화 한 식을 대입한다. 그러면 log안에 곱해진 항들이 있으므로 이를 log의 합으로 node 항과 edge 항을 분리해서 간단하게 적을 수가 있다.
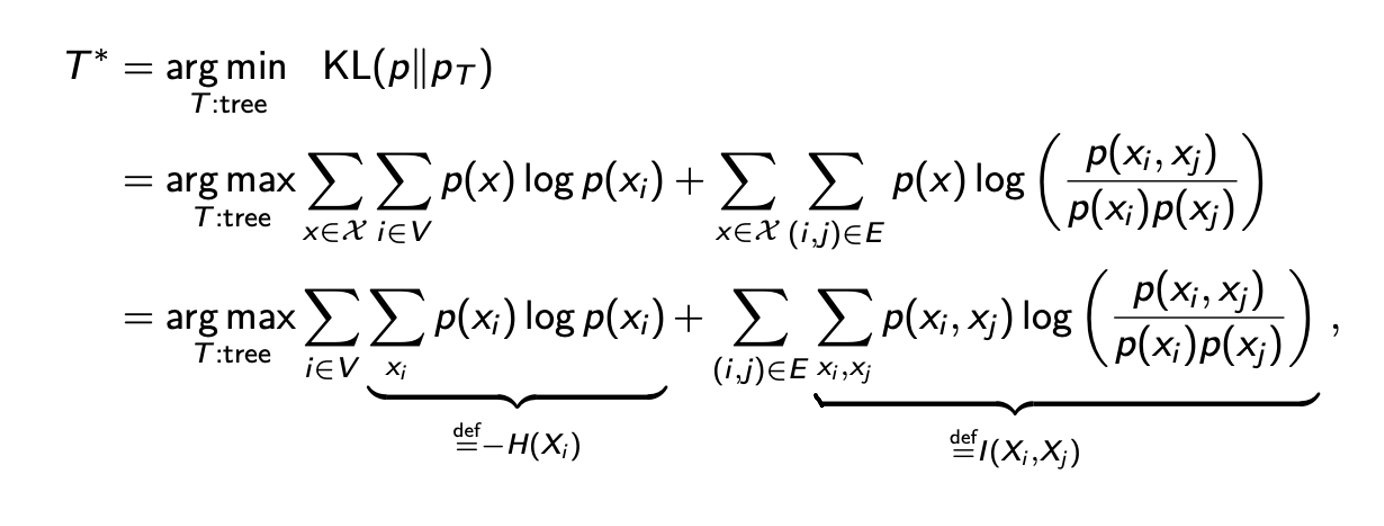우리는 graph의 모양을 최적화하고 싶다. 그래서 마지막 등호에서 첫번째 항은 어쨌든 고정될 것이다. 우리는 graph가 모든 random variable로 구성되어 있는지 알고 있어서 maximization의 첫번째 항에서는 변화하는 부분이 없다. 그래서 우리가 최적화 해야하는 부분은 오로지 두번째 항이다. 왜냐하면 두번째 항은 우리가 2개의 variable 사이의 edge를 그렸는지에 따라 변하기 때문입니다. 그래서 이 부분이 우리의 optimization problem이 된다.

더 나은 이해를 위해서 첫번째 항을 다른 tree가 존재하더라도 변하지 않을 것이라는 entropy $H(X)$에 대응시키고, 이는 무시할 것이다. 그리고 두번째 항을 2개의 variable간 mutual inforamtion의 합인 $I(X,Y)$에 대응 시킬 것이다. Mutual information을 이해하기 위해서, 만약 independent random variable이 있다고 했을 때, mutual independence는 0으로 계산 될 것이다. 이러한 경우에는 $p(x_i,x_j)$에 $p(x_i)p(x_j)$를 대입해서 log안을 1로 만들어서 항 자체를 0으로 만들 것이라는 이야기다.

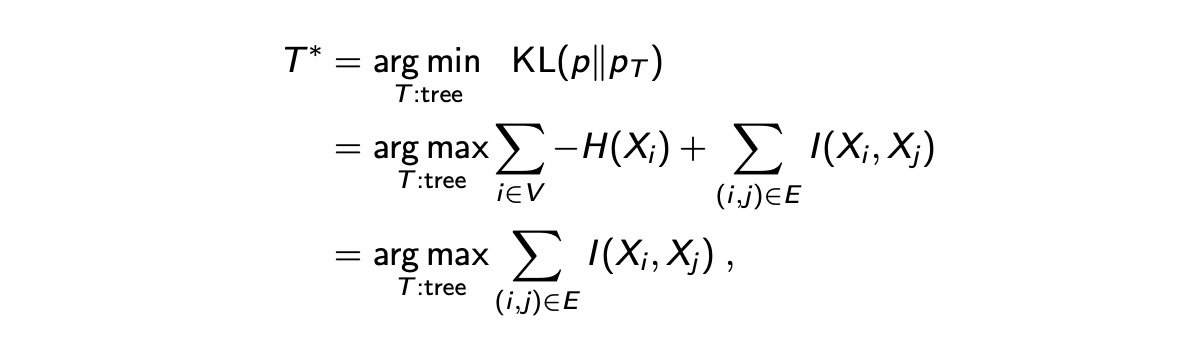요약하자면, 우리가 찾기를 원하는 최적의 approximation은 mutual information을 최대로 하는 tree graph이다. 어떤 의미에서는 pair-wise mutual correlation을 최대화하는 것이다. 왜냐하면 이는 가장 작은 error를 가지는 joint probability를 표현하는 것이 가능할지도 모른다. 이는 random variable 사이의 모든 dependence를 얻을 수 있다.

그래서 mutual information을 최대로 하는 것은 maximum weighted spanning tree(MWST)를 찾는 것으로로 이해될 수 있다. 우리는 tree graph에 관심을 가지고 있어서 maximization을 weight($w(i,j)$)가 mutual information($I(X_i,X_j)$)인 undirected complete graph의 MWST로 대응시킬 수 있다.

Chow-Liu Algorithm

Chow-Liu Algorithm은 weight를 mutual inforamtion으로 대체하는 MWST에 대응되는 KL divergence를 최소화하는 tree를 찾는 것이다. 이를 위해서 다음과 같이 algorithm이 동작한다.
Chow-Liu algorithm은 먼저 $X_i$와 $X_j$ 사이의 모든 mutual information $I(X_i,X_j)$를 계산한다. 그리고 MWST를 찾는 유명한 algorithm인 Kruskal greedy algorithm을 수행한다. 이 algorithm을 통해서 polynomial 시간 안에 weight를 최대로 만들 수 있다. 이는 곧 가장 큰 weight의 값을 찾는 것이다. 가장 큰 weight을 가지는 edge에서 시작하고 greedy하게 다음으로 큰 weight를 찾아가는 것이다. 이때 만약 edge가 cycle을 만든다면, 이는 제외하면 된다. 이렇게 계속하다가 edge를 총 $N-1$개를 찾았다면, Kruskal greedy algorithm을 멈추고 최적의 approximated tree를 output으로 하면 된다.

우리는 결론적으로 directed tree graph를 원하기 때문에 화살표 방향을 임의로 선택 된 root에서부터 설정해주면 된다. 마지막에 화살표를 정하는 과정을 제외하고 이전 과정을 전부 거치고 나면 undirected tree graph가 생길 것이다. 그러면 임의로 root node를 정해서 root node로부터 벗어나는 방향으로 화살표를 그려서 directd tree graph를 만들면 된다.

Example

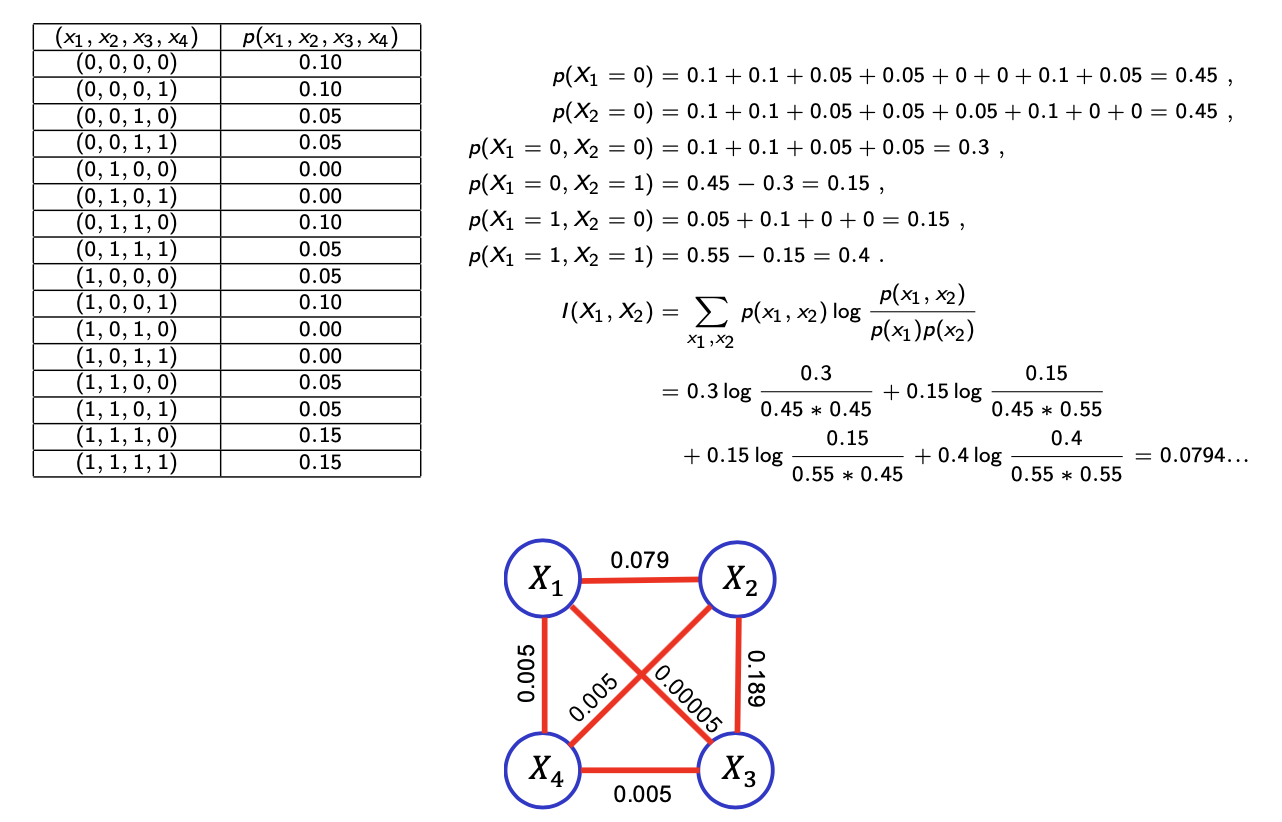예시를 보면 모든 random variable에 대한 empirical joint probability가 있고, 이로부터 marginal probability와 2개의 random variable에 대한 joint probability를 계산할 수 있다. 그러면 이제 모든 variable pair의 mutual information을 계산할 수가 있다. 그래서 edge weight를 mutual information으로 설정할 수 있고, 여기에 Kruskal greedy algorithm을 적용할 수 있다.

위의 예시에서는 0.189가 가장 큰 값이기에 이를 선택하고 다음으로는 0.079를 선택한다. 그 다음으로 0.005가 3군데 있지만, 임의로 하나를 고르면 된다. 여기서 멈춰야하는 이유는 다음 큰 값을 고르게 되면 cycle이 만들어지기 때문이다. 그래서 cycle이 만들어지지 않을 때까지 제외시키면서 선택하면 된다.
그래서 임의로 고르는 것이기 때문에 maximization problem에 대해서 여러개의 답이 나올 수가 있다. Edge의 방향을 무시한다면 위와 같이 3개의 답이 나올 것이다.

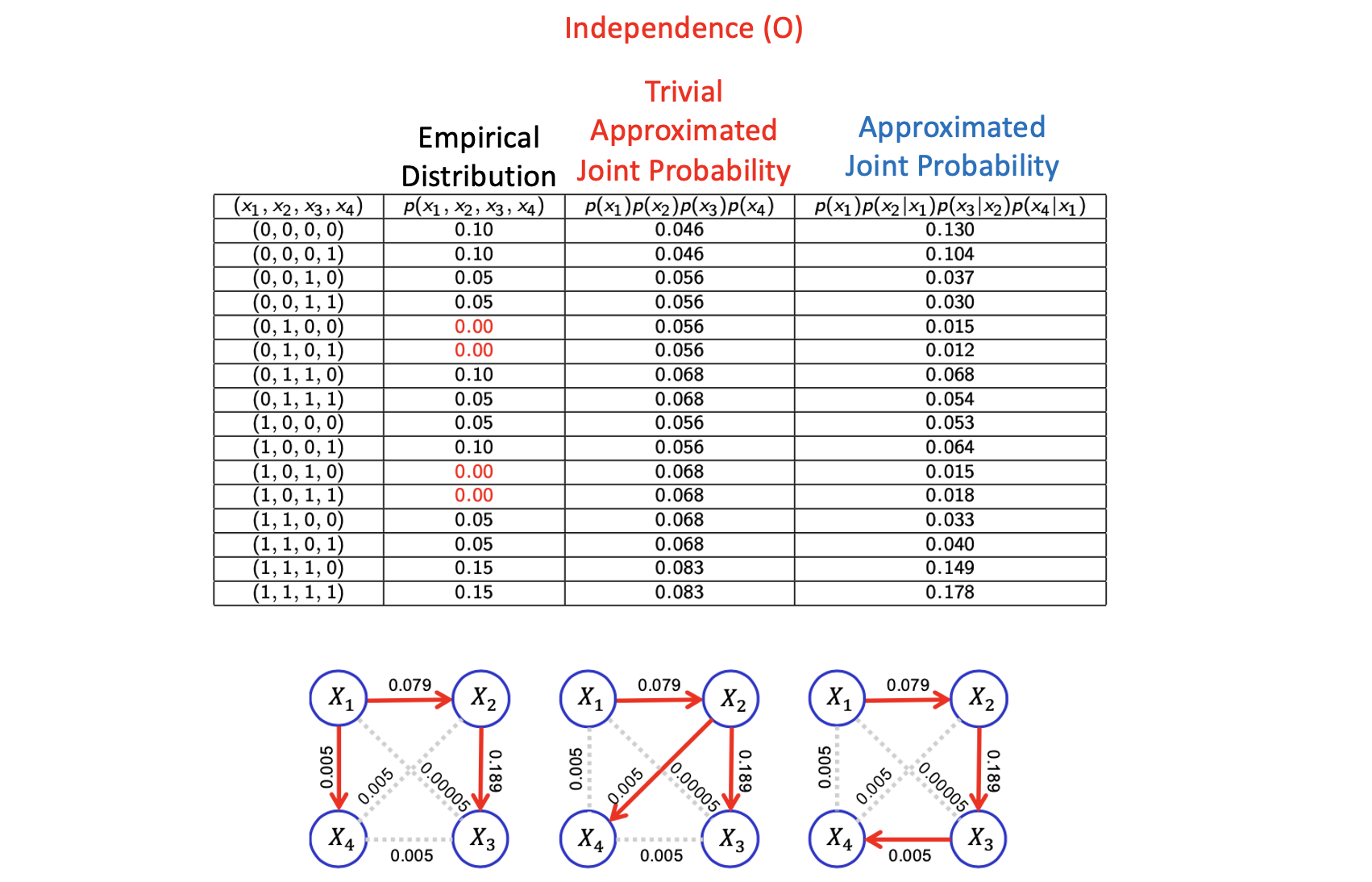
이 algorithm이 의미있는 tree를 만들었는지 확인하고 그 효율성을 보여주기 위해서 모든 random variable 사이의 independence를 가정하면서 trivial approximated joint probability와 우리가 approximation 한 결과를 비교할 것이다. 첫번째 graph에서 우리는 approximated joint probability를 얻었다고 해보자. 그리고 이 결과는 우리가 모든 variable에 대해서 independence를 가정했던 결과보다 empirical distribution에 더 가까운 것을 볼 수 있다. 특히, independence를 가정했을 때의 결과에서 아주 작은 값들이 empirical distribution에서 true가 되지 않는다. 왜냐하면 3번째와 4번째 configuration에서 empirical distribution이 0.05를 가져서 이 값이 1번째와 2번째 configuration보다 작은데, independence를 가정한 결과에서는 1번째와 2번째 값보다 크기 때문이다. 그래서 independence를 가정한 결과는 적절하지 못하다. 그러나 Chow-Liu algorithm의 결과는 approximation이 잘 된 것을 볼 수 있다.

5번째와 6번째를 보면 비록 dataset에서 configuration의 값을 놓치더라도, 즉 0이 나오더라도 우리가 approximation을 구하게 된다면 어느정도 양수를 가지게 된다. 누군가는 이를 좋아하지 않을 수 있다. 그러나 이는 이러한 joint distribution의 approximation의 구조를 가짐으로써 우리가 dataset에서 보지 못한 configuration에 대해서 의미있는 예측을 커버할 수 있음을 암시해준다.

Application to Pattern Recognition

손글씨를 이해하기 위해서 Chow-Liu algorithm을 적용할 수 있다. 0부터 9까지의 손글씨를 가지는 dataset이 있다. 각각의 손글씨는 각각의 픽셀 값이 0이나 1인 binary map 이미지에 대응시킬 수 있다. 그리고 이 이미지는 12와 8의 binary dot를 가지는 96차원이다. 그래서 이 이미지에 대해서 우리는 각각의 숫자에 대한 directed graph를 만들 수가 있다. 이로부터 새 이미지가 주어졌을 때, 우리는 그 이미지로부터 각각의 숫자에 대한 approximated joint probability를 계산할 수 있을 것이다. Bayes error를 최소화하기 위해서 다음의 classifier를 고려할 것이다.

위의 연산에서 숫자는 maximum approximated joint distribution을 보여주고, 숫자에 대한 prior distribution을 가지고 있어서 classifier의 decision을 개선할 수 있다. 다음은 숫자 4에 대한 graphical model의 예시이다.
이러한 식으로 계산을 해서 최대를 구하면 우리는 모든 tree graphical model을 구성해 classifier를 만들 수 있다.

Summary of Graphical Models: Pros and Cons

Undirected, directed graphical model 둘 다 분명한 장단점이 존재한다. 왜냐하면 unique한 conditional independece가 오직 undirected나 directed에 의해서 제공되기 때문이다. Undirected graph에서 우리는 시각적으로 conditonal independence를 전달할 수 있다. 여기서 "시각적으로"라는 것이 key point이다. Directed graph에서는 우리는 marginal probability나 conditional dependence를 시각적으로 설명할 수 있다. 그러나 여기서 설명하는 것들의 관계는 undirected graph에서 시각적으로 표현될 수는 없다. 어쨋든 우리는 동일한 joint probability를 undirected graph나 directed graph에서 적을 수 있다.

예를 들어, joint probability가 factorization에 의해서 표현되었다고 해보자. 이러한 관계식은 undirected graph에 의해서 표현될 수 있고, 완전한 graph를 가지는 것이 가능하다. 그러나 undirected graphical model을 사용하게 되면 x와 y 사이의 marginal independence를 알기 위해서 potential function을 면밀히 살펴야 한다는 문제가 있다. 반면 directed graph에서는 우리는 추가적으로 x와 y의 marginal independence를 검사할 필요가 없다. 단지 directed graphicla model을 그려서 x와 y가 marignal independence가 있다고 확인하면 된다. 그래서 이러한 차이점이 존재한다.

그리고 directed graphcial model에서 기술적인 제약이 존재한다. 우리는 directed graph에서 어떠한 cycle도 허락하지 않는다. 그리고 이는 directed graph에서 joint probability를 표현할 수 없다는 것을 함축하게 된다. Undirected graph에서 conditional independence에 따르면 joint probability를 potential function들로 나타낼 수 있지만, 불행히도 이렇게 관계식을 적는 것은 cycle를 반드시 포함하기 때문에 directed graph에서는 불가능하다. 그래서 이러한 factorization을 표현하고자 potential function마다 각각 2개의 후보군을 두고 판단할 때, 어떠한 지점에서 cycle이 존재할 수 있기에 directed graph에서는 표현이 불가능한 것이다.

그래서 중요한 것은 해당하는 joint probability에 해당하는 factorization의 시각화가 있는지에 대한 여부이다. Factor graph에서는 모든 factorization이 표현될 수 있다. 그러나 이렇게 표현할 수 있는 힘이 factor graph에 있다고 하더라도 directed graph와 비교했을 때 한가지 단점이 존재한다. Directed graph에서 marginal independence를 시각적으로 표현할 수 있다. 반면 factor graph에서는 모든 marginal independence를 시각적으로 나타낼 수 없다. 이러한 것은 directed graph에서나 가능하다.

Factorization을 factor graph에서 표현할 수 있지만, 시각적인 관점에서 2개의 random variable이 marginal independence를 가지는지 절대로 알 수 없다. 왜냐하면 만약 모든 random variable을 연결하는 factor에 대해 다소 non-trivial한 정의가 있는 경우에 우리는 marginal independence를 보장할 수 없다.