[기계학습] Graphical Model - Message Passing Algorithms on Factor Graph

Two Important Problems

Graphical model은 machine learning task를 다루는데 있어서 매우 유용하다. 특히 machine learning에서 우리는 종종 marginalization과 maximization을 다룰 필요가 있다.

Marginalization은 marginal distribution을 어떠한 data나 observation이 주어졌을 때 계산하는 것이다. Marginalization은 joint distribution을 marginal distribution으로 변환하는 것이다. 그러나 marginal summation은 주로 exponentail complexity를 수반하기 때문에 machine learning task를 다룰 때 힘든 부분이다.

예를 들어 우리가 $x_i \in {0, 1}$이고 우리의 model이 joint distribution $p(x_1, ..., x_N)$을 나타내고 있을 때, classification error 혹은 prediction error를 최소화하기를 원한다고 해보자. 이에 대해서 $x_i$의 marginal probability의 $\argmax_{x\in\{0,1\}}p(x_1=x)$를 계산해야 한다. 이는 $x_i$에 대한 optimal classifier이고, 이에 대해서 marginalization을 수행할 필요가 있다.

그리고 또한 우리는 joint value의 모든 configuration을 찾기를 원한다.

이를 위해서 marginal probability의 maximization을 생각할 수 있고, maximization은 $x_1$부터 $x_N$까지 기하급수적으로 많은 candidate를 취하게 된다. 그래서 일반적으로는 이 maximization은 계산적으로 다루기가 어렵다.

An Example of Factorization

그러나 factorization이 marginalization이나 maximization의 computational complexity를 반으로 줄여 줄 수 있다. 직관적인 이해를 위해서 다음의 간단한 5개의 random variable로 되어있는 joint probability의 factorization을 보도록하자.

그리고 이에 따른 factor graph는 다음과 같다.
4개의 factor가 존재하고, 각각의 factor는 neighboring variable들을 input으로 다루고 있다. 그래서 이 factorization에서 우리는 $x_2$의 marginal probabilibty를 다음과 같이 계산할 수 있다.
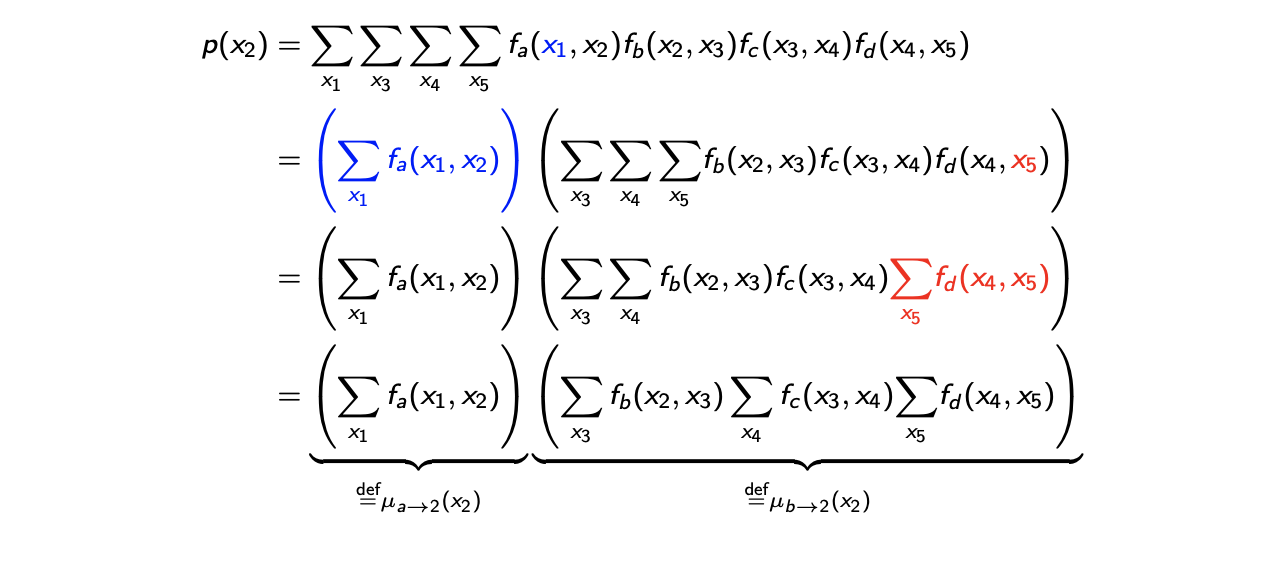처음에 marginalization은 random variable $x_2$를 제외한 summation을 취하게 된다. 그러면 $x_2$를 제외한 총 4개의 summation이 있고, 먼저 $x_1$을 유심히 보면 오직 첫번째 항에만 존재하는 것을 볼 수 있다. 그래서 첫번째 항을 $x_1$에 대한 summation 항으로 빼줄 수 있다. $f_a(x_1,x_2)$가 의미하는 것은 아마 $x_3,x_4,x_5$에 대해서는 상수로 고려될 수 있다. 그렇기에 두번째 등호에서 위와 같이 적을 수가 있다.

다음으로 볼 random variable은 $x_5$이다. $x_5$는 오로지 $f_d$에만 등장하기 때문에, 이를 해석해보면 $x_5$의 summation에서 $f_b,f_c$에 대해서 상수로 고려될 것이다. 그래서 세번째 등호에서 위와 같이 적을 수 있다.

이러한 방식대로 생각해서 마지막 등호와 같이 marginal summation을 적을 수 있다. Belief propagation algorithm을 쉽게 이해하기 위해서 첫번째 summation 항을 $\mu_{a\to 2}(x_2)$라고 정의하고, 나머지 항들을 $\mu_{b\to 2}(x_2)$라고 정의할 것이다. 이러한 notation은 factor a,b로부터 2로의 일련의 메시지이다.
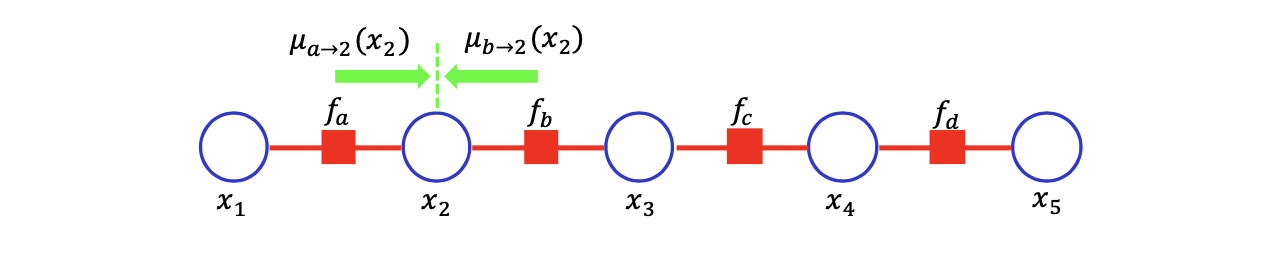Marginal probability를 메시지의 product 꼴로 적을 때 추가적으로 다른 모든 marginal probability를 메시지의 product 꼴로 적을 수가 있다.

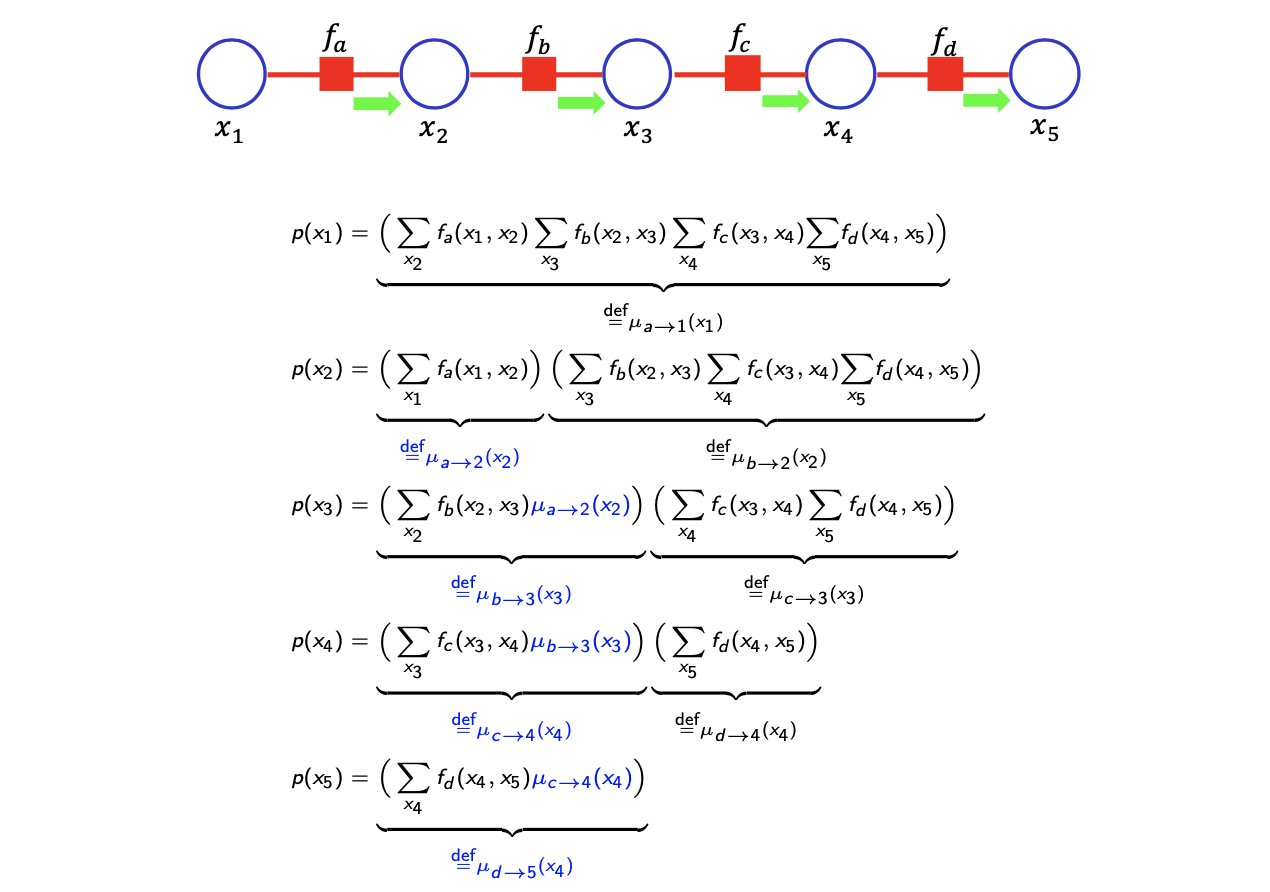
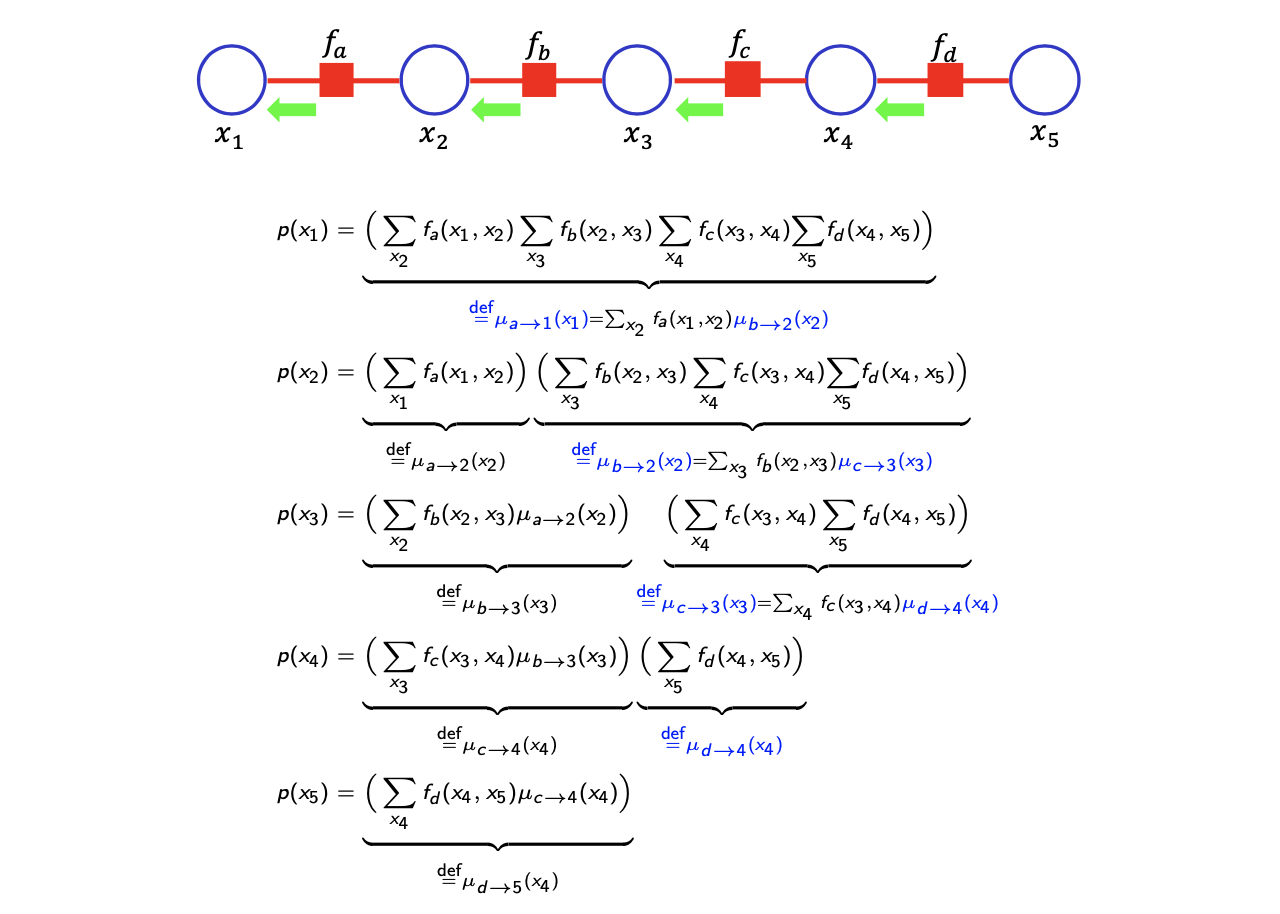여기서 메시지는 관심 있는 variable 방향으로 적으면 된다. 예를 들어 $x_3$의 marginal probability에 대해서 적을 때, 위에서 봤던 논리에 의해서 $x_3$의 이웃하는 factor가 $f_b,f_c$이기에 $b\to3$와 $c\to3$ 방향으로 일반화 할 수 있다. 특히 message가 recursive한 방식으로 확인할 수 있다. $x_2$에 대해서 계산을 했다면 이를 이용해서 $x_3$를 recursive하게 나타낼 수 있다. $x_1$에 대한 summation 항을 $\mu$로 대체할 수 있다. 이렇게 모든 marginal probability에 대해서 적용하게 되면 주목하고자 하는 variable 방향으로 쉽게 메시지의 product 꼴로 적을 수가 있다. Marginalization은 메시지의 함수로 나타낼 수 있고, recursive한 방식으로 정의될 수 있다.

An Efficient Marginalization via Factorization

지금까지 본 내용들을 일반화하여 그 효율성을 보도록 할 것이다. Random varialbe이 N개가 있을 때, 다음과 같이 joint probability를 line factor graph로 나타낼 수 있다.

이때 하나의 random variable $x_i$에 대해서 marginal probability는 다음과 같이 2개의 메시지의 곱으로 나타낼 수 있다.

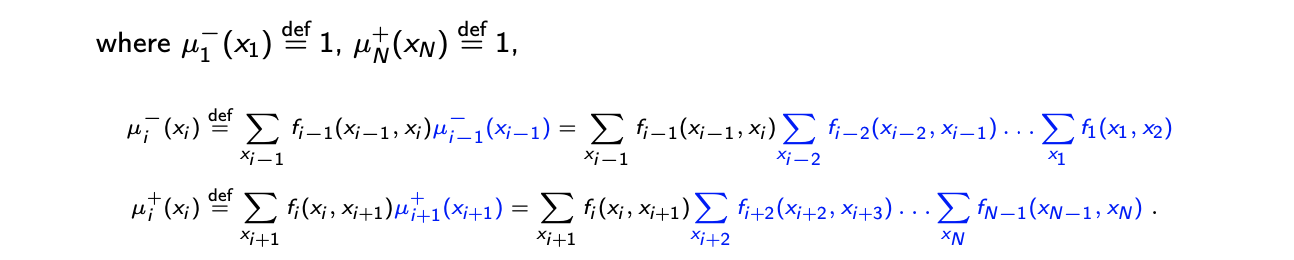
지금까지 간단한 예시를 통해서 factor graph가 있을 때 marginalization에 대해서 알아보았는데, joint probability의 구체적인 식을 통해서 우리는 marginal probability를 computational complexity의 관점에서 쉽게 계산할 수 있었다. Marginal probability를 계산하는데 있어서 다른 random variable의 marginal probability를 공유할 수 있었다. 그러다보니 marginal probability를 계산하는데 있어 쉬워지게 되고, 각각의 계산이 기하급수적으로 증가하지 않게 된다. 대신에 marginal probability를 계산하는것이 linear하게 줄어들게 되었다. 이러한 것들은 variable과 factor가 번갈아 나타나는 line factor graph일 때 유효하다. 이러한 구조일 때 메시지라는 notion을 통해서 쉽게 marginalization을 계산할 수 있게 된다.

An Intuitive Understaning

다음은 메시지를 직관적으로 쉽게 해석한 것으로 학생 수를 줄지어 세는 간단한 프로토콜이다. 아마 거의 모든 사람들이 어디 캠프같은 곳을 갔을 때 이러한 경험을 해봤을 것이다.
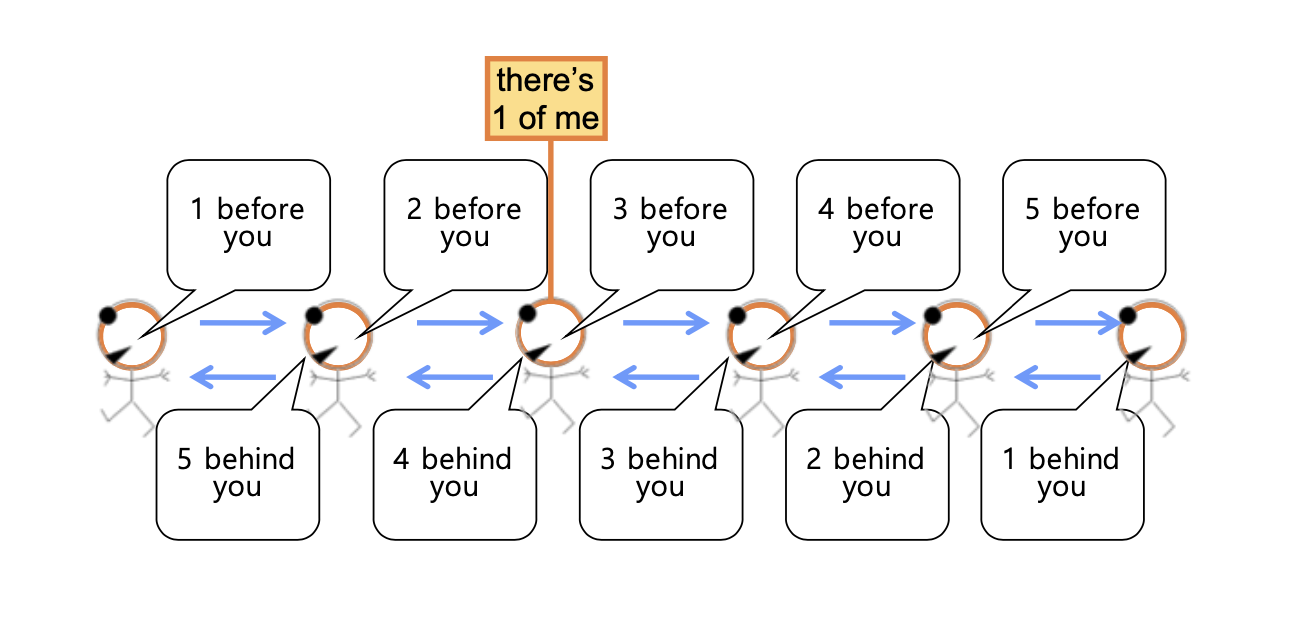첫번째 사람은 두번째 사람에게 자기 자신만을 카운트하여 그 정보를 전달해준다. 그리고 두번째 사람은 세번째 사람에게 자기 자신을 더해서 그 정보를 전달해준다. 이러한 식으로 message를 전달하고나서 마지막 사람은 다시 이전 사람에게 message를 보내게 된다. 그렇게 해서 다시 첫번째 사람에게 message가 전달이 되고, 중간에 모든 사람들은 자신의 앞과 뒤에 몇 명이 있는지 알게 된다. 그래서 모든 사람들이 앞과 뒤에 있는 사람의 수를 더해서 총 학생의 수를 알 수 있게 된다. 이러한 반복적인 계산은 직관적으로 이해 될 수 있다.

Sum-Product Belief Propagation(BP) in Tree

그래서 이러한 것들은 line graph에 대한 것이고, 이제부터 우리는 line 형태보다 좀 더 복잡한 graphcal model을 다뤄야 한다. 이러한 경우에 대해서 우리는 이전에 본 message passing algorithm을 일반화 할 수 있다. 그것이 바로 sum-product belief propagation이고, factor graph가 tree 모양일 때 marginal probability를 계산하기 위해서 등장했다. 여기서 tree라는 것은 loop나 cycle이 없는 것을 말한다.

Factor graph가 tree의 형태로 주어졌을 때 우리는 다음과 같은 방식으로 marginal probability를 계산할 수 있다. 이를 위해서 $\partial(node)$를 set of neigbors로 정의하고, 단순함을 위해서 $x_I$를 벡터의 concatenate 형태로 $\{x_i\}_{i\in I}$라고 정의 할 것이다.

그러면 이제 sum-product BP가 factor로부터 variable까지의, variable로부터 factor까지의 message를 계산한다. 구체적으로 우리는 $\mu_{u\to i}(x_i)$를 factor $f_u$가 variable $x_i$로 보내는 message로 정의할 것이다. 그리고 $\nu_{i\to u}(x_i)$를 variable $x_i$가 factor $f_u$로 보내는 message로 정의할 것이다.

Factor에서 variable로 보내는 message $\mu$는 위와 같은데, 식을 보면 다른 variable로부터의 message들인데 각각의 factor가 variable로 보내는 message는 receiver인 $i$를 제외한 neighboring variable들로부터 marginalized 되어 있다. 반대로 variable이 factor로 보내는 message는 다소 간단하다. 식을 보면 단지 receiver인 factor $u$를 제외한 neighboring factor로부터 variable로 보내는 모든 message를 곱한 형태를 취한다. 만약 우리가 tree graph를 생각한다고 했을 때 initialization은 전혀 고려할 필요가 없다. 어쨌든 leaf variable이나 leaf factor에 대해서는 product 연산을 할 것이 없다. 이는 empty set의 product는 전형적으로 1로 정의가 된다. 그래서 leaf variable은 neighboring factor로 1이라는 message를 보내게 된다. 마찬가지로 leaf factor는 자신과 연결이 된 다른 variable이 없고 오로지 하나의 receiver variable만 있기 때문에 $\mu$의 식에서 product 값이 1이 되어 오로지 해당하는 factor 값만 바로 보내게 된다.

이제 모든 $\mu$와 $\nu$를 계산하고 나면 $x_i$의 marginal probability가 위와 같이 계산 될 것이다. 이때 등호가 아니라 비례한다고 보는 것이 더 정확한 표현이다. $p(x_i)$는 $x_i$로 향하는 모든 message의 곱으로 계산된다.

이는 이전에 살펴본 line graph에서의 message passing을 일반화한 것이다. 이를 확인하는 것은 다소 어렵지만 line graph에서의 message passing algorithm을 보다보면 쉽게 알아낼 수 있을 것이다. 여기서 사실 line graph도 cycle이 없기 때문에 일종의 tree이다.

그래서 지금까지 본 이 algorithm의 이름은 sum-product belief propagation(BP)이다. 이 algorithm에서 message의 식이 sum과 product의 형태로 되어 있는 것을 볼 수 있다. 그래서 이름이 sum-product BP가 된 것이다. 그러면 belief와 propagation도 궁금할 것이다. Propagation은 graph 상에서 message를 줄줄이 전달하는 것을 의미한다. 그리고 belief가 의미하는 것은 message가 marginal probability에 대해서 일종의 local belief로 이해될 수 있다는 것이다. $\mu{u\to i}$라는 message에 대해서 이 message는 factor 뒤에서 일종의 belief의 요약체로 이해되는 것이다.
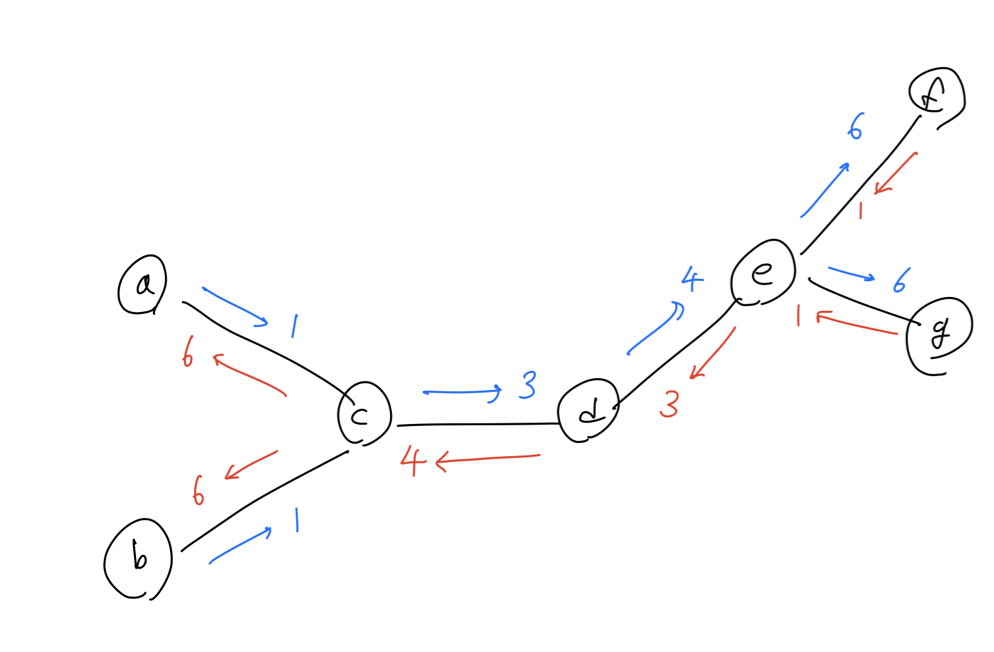BP에 대한 더 나은 이해를 위해서 위와 같은 tree graph를 생각해 볼 수 있다. 그러면 message passing rule은 가장 좌측에 있는 사람 a, b는 1이라는 message를 c에게 전달하게 될 것이다. 그러면 이를 받은 c는 자신을 포함해서 3이라는 d에게 message를 전달할 것이다. 다시 이를 받은 d는 자신을 포함해서 4라는 message를 e에게 전달하게 된다. 마지막으로 4를 전달 받은 e는 g로부터 1을 다시 받아 f에 6을 전달하고, 마찬가지로 f로부터 1을 다시 받아 g에 6을 전달할 것이다. 그러면 e는 자신을 포함해서 3이라는 message를 d로 보내고, d는 다시 4를 c로 보낼 것이다. 이전과 마찬가지로 c는 4에다가 a가 보내는 1과 자신을 더한 6이라는 message를 b로 보내고, 이와 같은 방식으로 a에도 6을 보낼 것이다.

이런식으로 cycle이 없는 graph가 주어졌을 때, 우리는 항상 분산하여 node의 총 개수를 계산할 수 있다. 이러한 종류의 계산이 sum-product BP를 요약했다고 보면 되고, 이는 직관적으로 이해하는데 도움이 될 것이다. 그래서 message를 계산하기 위해서는 모든 incoming message를 고려해야 한다. 그래서 가장 좌측 끝에 마지막 사람은 자기 자신과 전달받은 6이라는 message를 더해서 총 7이라는 결과를 내고, 이는 전체 사람의 수에 해당하게 된다. BP는 marginalization을 분해하면서 marginal probability를 계산하려고 시도했고, 위에서 defg를 marinalization한 결과는 c로 보내는 4라는 message로 귀결하게 된다. 그리고 abc를 통해서 message를 계산하게 되면 3이 되는데, 여기에 e가 d로 보내는 message 3까지 해서 d에 대한 marginal probability를 d로 향하는 message들을 곱해서 구할 수가 있다.

Scheduling in Sum-Product BP on Tree

Message가 이전에 계산된 message를 필요로 하는 것은 분명하다. 그래서 message passing의 scheduling은 사소한 것이지만, 분명함을 확인하고자 scheduling 절차를 다음과 같이 보려고 한다.
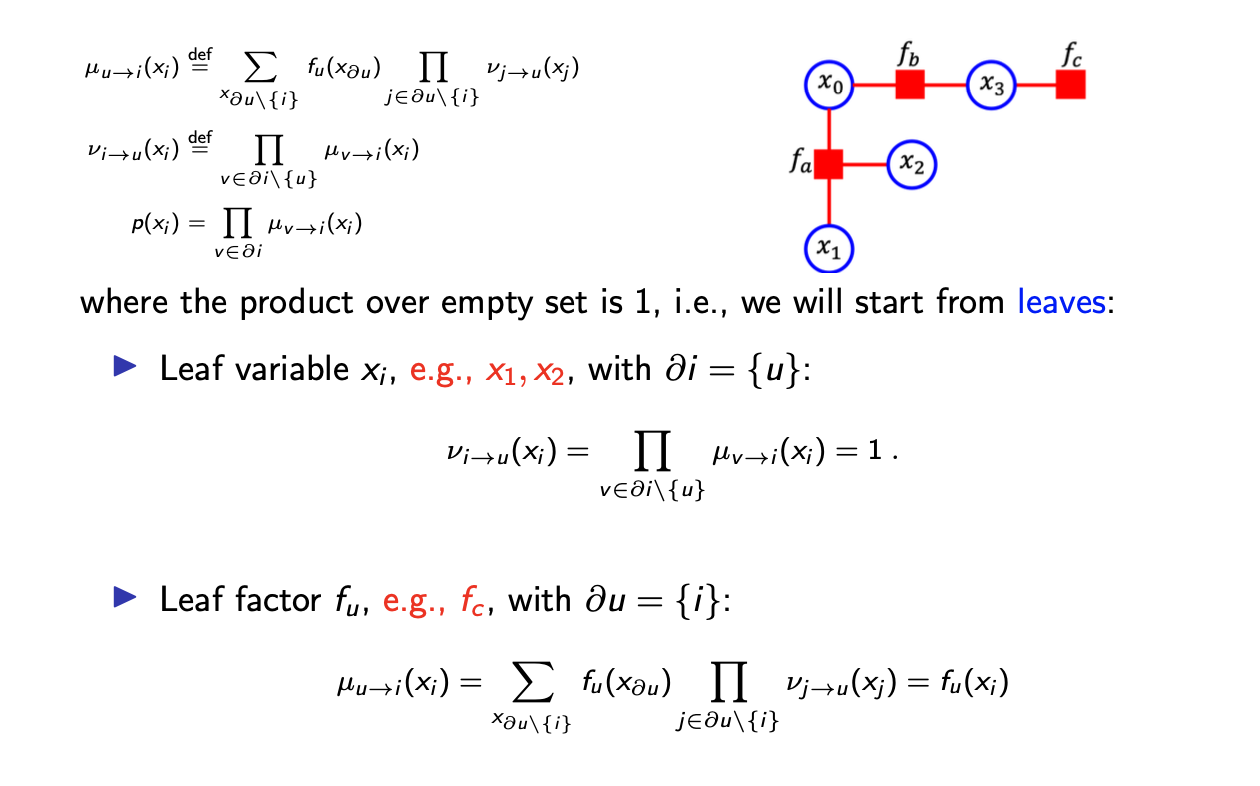만약 variable이 leaf라면 이 variable로부터의 모든 message $\nu$는 1이 된다. Factor에 대해서 만약 leaf라면 자기 자신의 factor를 그대로 message로 보내게 된다. 우리가 leaf variable로부터 factor로 message를 받게 되면, 우리는 대대로 message를 계산할 수 있다.

Example of Sum-Product BP

지금부터는 sum-product BP를 cycle이 없는 간단한 graph 예시를 통해서 보도록 하자.
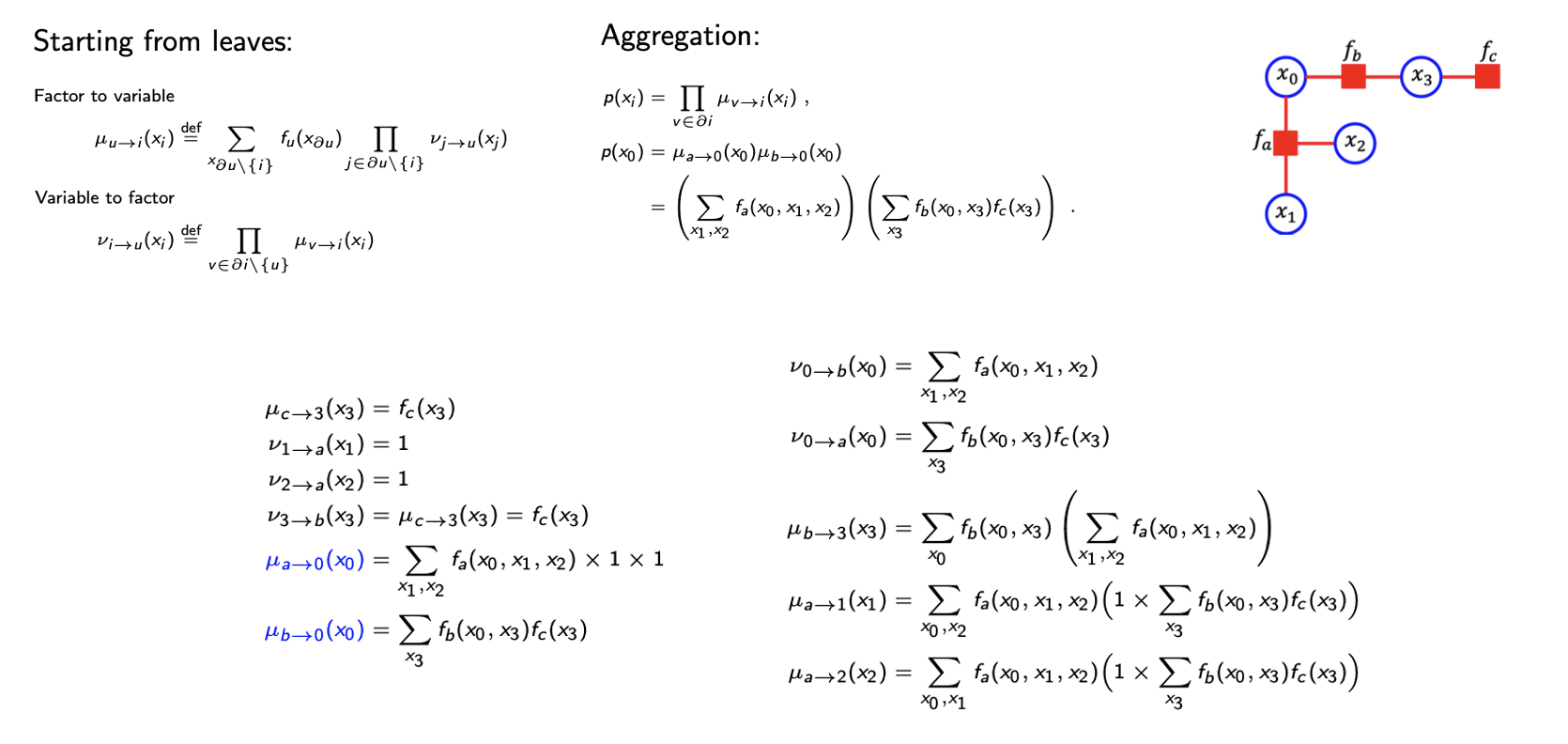시작은 leaf variable과 leaf factor의 initialization으로 한다. 그 다음으로 leaf variable과 leaf factor의 message를 이용해서 두번째 message를 계산한다. 그리고 두번째 message를 이용해서 다음 message를 계산한다. 이러한 식으로 계속하다보면 우리는 정확히 marginal probability를 계산할 수 있게 된다. 이 내용은 이렇게 넘어가겠지만, 디테일들을 따라가면서 BP algorithm을 배우는 법을 확실히 이해하면 좋다.

Loopy Sum-Product BP

이러한 sum-product BP는 원래는 tree graph를 위해서 생겨났다. 왜냐하면 cycle이 없는 factor graph에 대해서 우리는 sum-product에 의한 marginalization을 보장할 수 있었다. 그러나 모든 것이 순탄하게 흘러가지는 않았다. 그래서 여러 factor graph에서 loop나 cycle이 얼마든지 많이 존재할 수가 있다. 이에 대해서 생각한 것이 바로 비록 정확성(exactness)이나 수렴성(convergence)를 일반적으로 보장하지 않더라도 cycle의 존재성을 무시한 loopy sum-product BP이다.

Loopy sum-product BP algorithm은 다음과 같이 설명할 수 있다.
먼저 임의로 message들을 initialization을 진행한다. 일반적으로 leaf factor 자신을 message로 하여 1이 되게 하거나, 1을 message로 하는 leaf variable을 선택하게 된다. 그리고는 반복적으로 message를 동기화하여 update를 해준다. 이는 모든 message들이 이전의 message를 사용해서 update가 된다는 것을 의미한다. 우리는 $\mu^{(k)}$와 $\nu^{(k)}$를 k번째에 대한 message로 정의할 것이다. 이 message를 이용해서 k+1번째의 message를 sum-product BP의 방식처럼 계산하여 update 할 것이다. 이렇게 계속 함으로써 때떄로 우리는 특정 값에서 message의 convergence를 볼 것이다. 그래서 이러한 convergence를 본 순간 algorithm을 멈추고 각각의 variable $x_i$에 대해서 marginal probability를 approximation을 하면 된다. 즉, $b_i$를 variable $x_i$로의 모든 message를 곱해서 계산하면 된다.

여기서 중간에 algorithm을 멈춘다고 했는데, convergence에 대한 보장이 없기 때문에 언제 멈추는지 궁금할 수 있다. 반복하는 횟수에 대해서 upper bound를 $K$라고 하거나($k < K$) message 사이의 difference를 최대로 하도록 계산하여 $\epsilon$ 값보다 큰 경우에는($max_{i,v}\|\mu_{v\to i}^{(k)} - \mu_{v\to i}^{(k+1)}\| > \epsilon$) 더 많은 반복을 해야할지도 모른다. 이러한 조건들이 loopy sum-product BP의 멈추는 조건이 된다.

Loopy sum-product BP는 정보 이론과 같은 여러 시스템에서의 exactness를 증명해왔다. 여기서 sum-product BP나 marginalization이 signal이 주어졌을 때의 latent symbol을 예측하는데 사용된다. 우리는 항상 sum-product BP의 convergence나 exactness를 오직 message의 intialization이 exact했을 때만 보장하고 싶다. 만약 어떻게든 marginalization 등을 계산했고, 모든 message들을 부분적으로 marginalization 한 값에서 initilazation 했다면 우리는 convergence나 exactness를 보장할 수 있게 된다. 이러한 이유가 여전히 loopy sum-product BP algorithm이 사용되어져 온 이유이다. 그래서 지금까지 marginalization에 대한 BP algorithm에 대해서 알아보았다.

Maximization via Factorization

Machine learning에는 2개의 근본적인 계산이 존재한다. 하나는 marginalization이고, 그리고 나머지 하나는 지금부터 살펴 볼 maximization이다. Marginalization에서 살펴 본 BP 아이디어를 maximization task에도 적용할 수 있다.

Maximization은 joint probability를 최대로 하는 random variable의 configuration을 찾는 것이다.
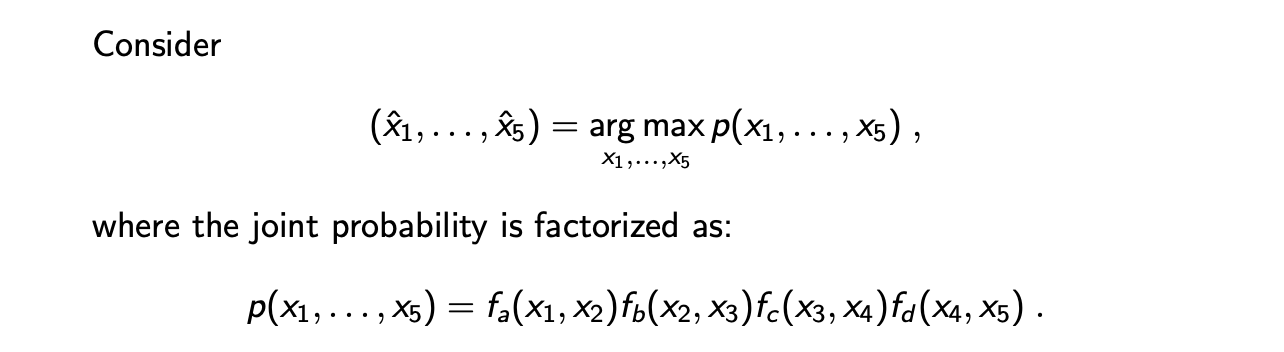여기서는 variable 이름을 x로 사용했지만, 만약 optimal hyperparameter를 찾는다고 했을 때에 이러한 내용을 적용하여 찾으면 된다. 이러한 maximization 문제를 풀고 싶고, $x_1$부터 $x_5$까지 모두 binary 일 때, 간단한 방법으로 모든 configuration을 확인해보면 된다. 더불어 joint probability가 line graph처럼 factorization form으로 분해가 된다고 가정할 것이다. 우리는 line graph에서 factorization을 사용해서 모든 variable들에 대해서 maximization을 local maximum으로 분해할 것이다. 이를 위해서 marginalization에서 보았던 방법과 비슷하게 다음과 같이 식을 변형할 것이다.
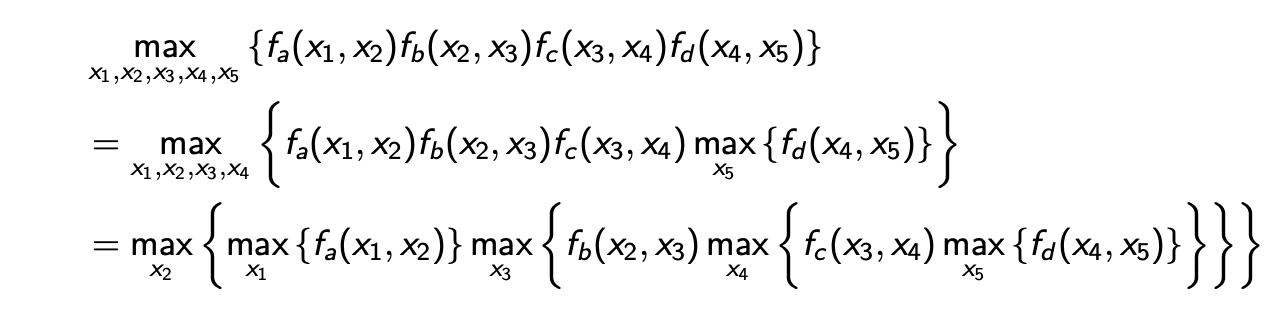$f_d$만이 $x_5$와 관련이 있어 $x_5$에 대해서 max 연산을 $f_d$에 취할 것이다. 이러한 식으로 계속해서 적용하면 마지막 등호와 같이 maximization 식을 정리할 수 있다. 이렇게 하면 계산 양을 줄여줄 수 있다. 왜냐하면 각각의 maximization이 단지 random variable에 대해서 0인지 1인지만을 비교하게 되기 때문이다. 그러므로 이는 computational complexity를 줄여주는 효과가 있다.

Max-Product Belief Propagation(BP) in Tree

그래서 max-product BP는 tree graph로 확장될 수 있고, 우리는 max-product BP의 exactness를 보장할 수 있다. 이름에서 보다시피 sum-product일 땐 summation과 product 연산을 했지만, max-product BP에서는 max 연산과 product 연산을 하게 된다. 그래서 sum-product BP와의 유일한 차이점은 factor에서 variable로의 message 계산에서 summation 연산 대신 max 연산을 하는 것이다.
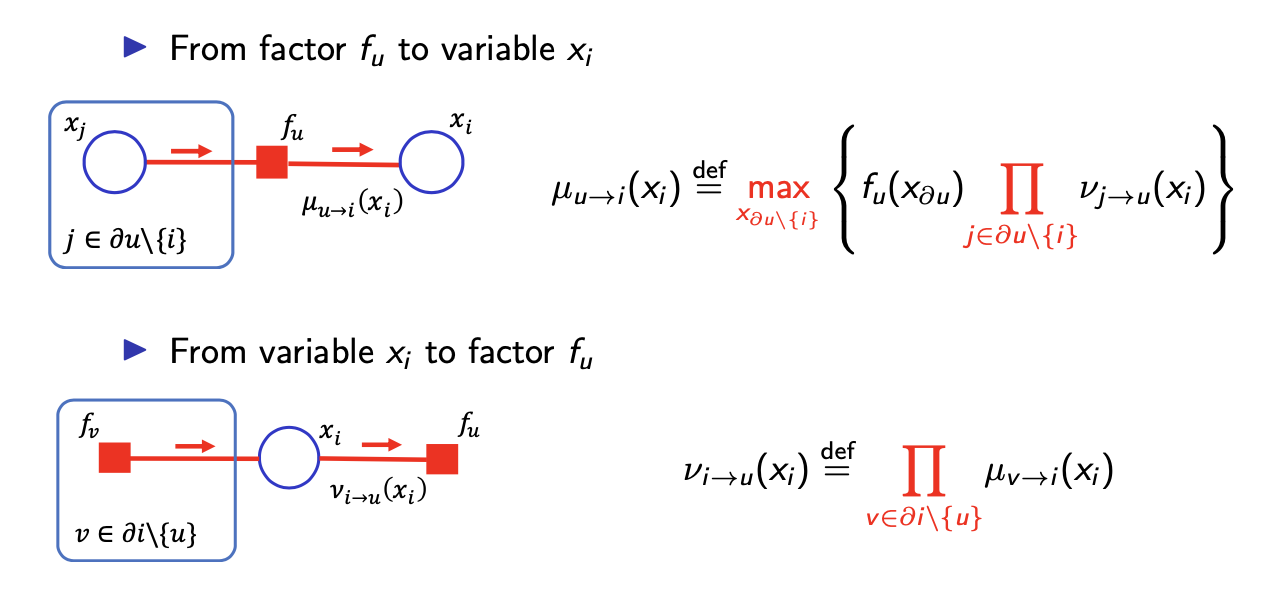그러면 max probability는 $p_{max}=\operatorname*{max}_{x_i}\{\prod_{v\in\partial i}\mu_{v\to i}(x_i)\}$를 계산하여 찾을 수 있다. 모든 variable node로부터 maximum probability를 계산할 수 있고, 대응되는 local configuration이 global configuration으로 가게된다.

Scheduling in Max-Product BP on Tree

다음은 max-product BP에서의 scheduling이고, 이는 sum-product BP와 똑같은 메커니즘이다.
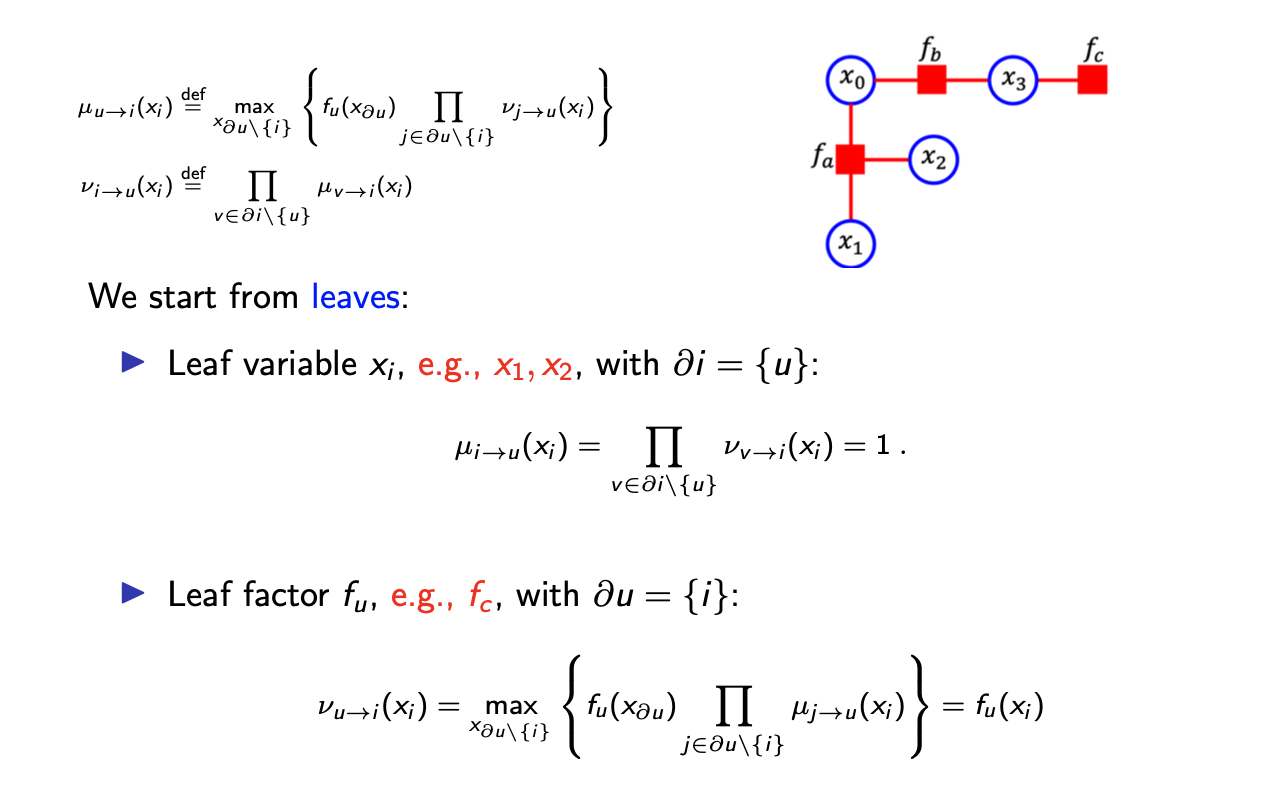시작은 leaf에서 하고 그 값은 leaf variable은 1, leaf factor는 factor로 initialization하면 된다.

Example of Max-Product BP

그리고 다음은 max-product BP의 예시이다. Sum-product BP에서처럼 직관적으로 이해하기 위해서 max-product BP에서도 간단한 예시를 들어보도록 할 것이다.
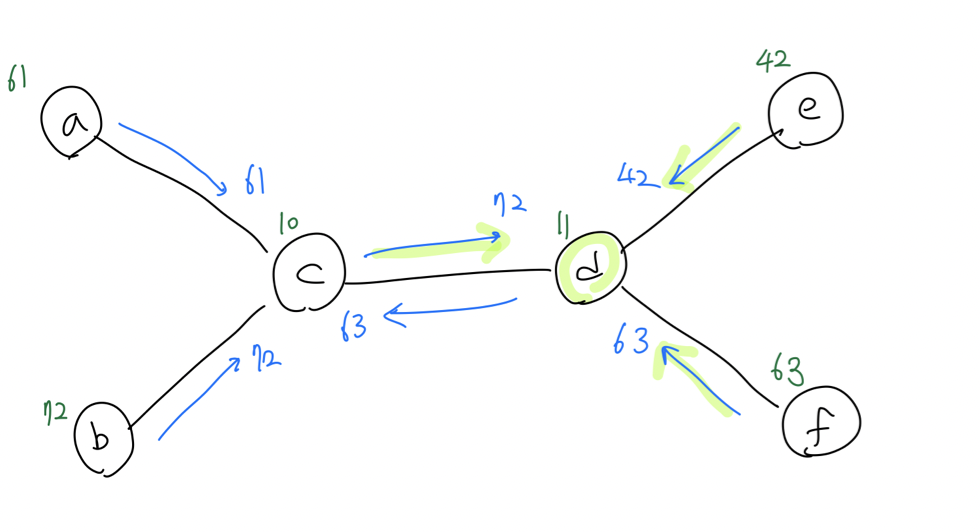위의 graph에서 각각의 node는 중간고사 점수라고 해보자. 여기서 우리가 찾고 싶은 것은 누가 중간고사에서 가장 높은 점수를 받았는지이다. 이 graph에서 최고점을 찾기 위해서 message passing algorithm을 이용할 것이다. 먼저 b가 c에게 72라는 message를 전달했다고 하자. 그리고 a는 c에게 61이라는 message를 전달했다고 하자. 마찬가지로 e와 f도 d에게 각각 42와 63을 전달할 것이다. 그러면 이제 c가 d에게 message를 전달할 때, d라는 사람 이전에 점수들을 비교하여 최고점을 전달할 것이다. 마찬가지로 d도 c에게 c라는 사람 이전에 점수들을 비교해서 최고점을 전달할 것이다. 그리고 이제 d라는 사람은 72점이 최고점이라는 것을 d로 향하는 점수들과 자신의 점수를 비교해서 알아냈을 것이다. 이러한 방법은 max-product BP를 직관적으로 이해하는데 도움이 된다. 만약 loop가 있다면, 계산은 절대로 수렴하지 않을 것이다. Tree 모양의 factor graph가 주어진다면 우리는 maximization의 convergence와 exactness를 보장할 수 있다.

위의 에시는 천천히 따라가면서 확인해보면 된다.

Max-Sum BP in Tree

Max-product는 모든 joint probability에 logarithm을 취해서 똑같이 max-sum BP로 변환할지도 모른다. 그리고 이 내용은 다음과 같다.
우리는 joint probability가 factor의 곱으로 표현되는 것을 알고 있다. 그래서 여기에 log를 취하면 product 연산이 summation 연산으로 대체되는 것을 볼 수 있다. Sum-product BP에서 이러한 아이디어가 쉽게 일반화 되지 않지만 특별한 경우에 대해서 적용이 가능하다.