[기계학습] Graphical Model - Visualization of Statistical Models 2

Conditional Independence

지금부터는 우리가 graphical model을 그릴 때 무엇을 할 수 있는지에 대해 알아보고자 한다. 그 중 하나로 graphcial model을 그리고 conditional independence를 확인할 수 있다. Z가 주어졌을 때 X와 Y가 conditonally independent하게 되면 다음과 같이 나타낼 수 있다.

이는 "X perpendicular Y given Z"라고 읽으면 되고, 이것이 의미하는 바는 다음의 식을 통해서 알 수 있다.

$\text{Proof}$

z가 주어졌을 때 x, y의 conditional joint probability는 각각의 marginal conditionaly probability의 곱으로 나타낼 수 있으며, 같은 의미로 이 식은 2개의 식으로 나눠서 표현할 수 있다. 이는 우리의 가정하에 true가 되고 이것이 conditional independence의 정의이다. 그리고 일반적인 independent는 condition이 empty set인 marginal independence이다.

이와 같은 정의로는 empty condition은 무시하기 때문에 다음의 conditional independence가 있다.

Examples of Conditional Independence

Conditional independence의 예시들을 보면서 이를 사용함에 따라 생기는 유용함에 대해서 이해해보도록 하자.
아마 벌금과 차의 종류는 서로 depedent 할 것이다. 아무래도 차가 좋을수록 속도가 더 빠를 것이기 때문이다. 그러다보면 과속하기도 쉬울 것이다. 그래서 벌금의 양은 이에 비례하여 증가할 것이다. 이렇게 차의 가격과 벌금의 양에 대해서 positive correlation에 대해서 생각해볼 수 있다. 그런데 차의 속도에 대해서 보게 된다면 차의 종류와 벌금의 양은 서로 independent하다는 것을 알게 될 것이다.

이와 비슷하게 폐암과 누런이는 서로 관련있어 보인다. 그런데 random variable을 볼 때 담배를 피는 것을 알게 된다면 우리는 아마 폐암과 누런이 사이의 conditional independence를 주장할 수 있을 것이다. 담배 핀다는 사실을 모른다면 폐암과 누런이는 서로 상관관계가 있을지도 모르지만, 일단 해당하는 사람이 담배를 폈다면 폐암이나 누런이가 이제는 담배로부터 생겼을지도 모른다고 생각하게 된다. 그래서 폐암이 누런이가 원인이 아닌 담배가 원인이 되는 것이다. 반대로 누군가가 담배를 피지 않는다면 아마도 누런이는 유전적인 원인일 가능성이 크고 다른 원인에 의해서 폐암에 걸렸을 것이라고 판단할 것이다. 그래서 담배라는 원인이 폐암과 누런이라는 2개의 random variable에 대해서 더 independent하게 만드는 것이다.

Marginal independence는 conditioanl independence를 내포하고 있지 않다. 위의 2개의 예시는 2개의 random variable이 marginal independence가 아니지만, 어떠한 좋은 관찰이 있을 때는 conditional independence가 된다. 그러나 종종 다른 경우에 대해서 2개의 random variable이 서로 marginal independence 하지만 어떠한 관찰이 주어졌을 때 이들은 conditional independence하지 못하는 상황들에 마주치게 된다.

예를 들어 어떠한 관찰도 없고 알지도 못했을 때 A와 B라는 2개의 팀의 실력이 서로 independent하다고 할 수 있다. 그러나 어떠한 게임에서 A가 B를 상대로 이겼다는 사실을 알게된다면 서로의 실력은 이제는 independent하다고 할 수 없다. 이렇게 conditioanl independence는 매우 흥미롭고 우리는 independence가 추론에 있어서 계산이 가능하도록 만들어서 쉽게 평가할 수 있게 된다. 그래서 우리가 멋진 conditional model과 observation 설정을 만들게 된다면 최종적으로 computation complexity를 줄일 수 있게 된다.

Conditional Independence in Graphical Model

그래서 conditional independence는 매우 흥미로운 이야기이다. 특히, conditional independence는 우리가 관찰해야하는 것과 배우는 방법에 대해서 어떠한 힌트나 영감을 제공해준다. 어떠한 independence도 computational marginalization, computational MAP, computational estimation 등에 대해서 더 쉽게 만든다고 이야기했었다. 그래서 필요한 것은 더 observable 한 random variable이나 그러한 computation을 쉽게 만드는 것이고 이것은 우리가 무언가를 탐지하기 위해서 어떠한 센서를 넣어야 하는지에 대한 가이드라인을 만든다.

예를 들어서 포스코 공장에서 어떠한 센서를 놓음으로 인해 비정상적인 것을 탐지하기 원한다고 해보자. 이 공장이 문제가 있는지 없는지 결정하기 위해서 어떠한 센서를 놓고 싶을 것이다. 동시에 conditioanl independence를 기반으로 어떠한 종류의 센서를 놓아야할지와 어디에 놓으면 좋을지에 대해서 생각해 볼 것이다. Conditional independence를 생각하게 되면 graphical model은 단순한 설명 제공이 가능하다. 예를 들어 3개의 random variable이 있을 때 굳이 graphical model을 그리지 않고도 쉽게 설명할 수 있고 이해할 수 있었다. 그러나 random variable의 수가 많아지게 되어 conditional independence가 복잡해지면 graphical model은 이들의 관계를 설명하는 좋은 도구가 된다.

Markov Property in Undirected Graph

구체적으로 undirected graph는 매우 직관적이다. Undirected graph가 주어진다면 2개의 random variable이 conditional independence 한지 아닌지 2개의 random variable이 condtion에 의해서 block이 됐는지에 따라 쉽게 확인할 수 있다.

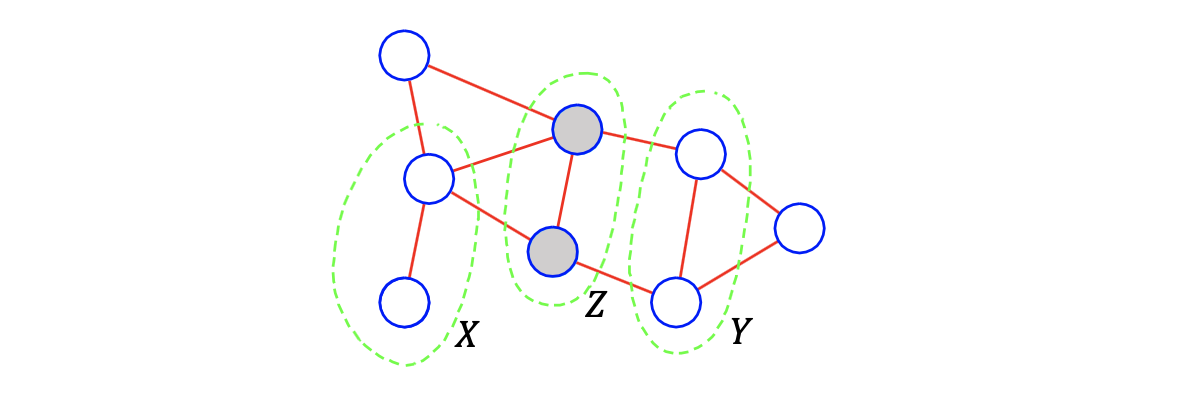위와 같이 8개의 random variable이 주어졌을 때, 중간에 $Z$가 neural network의 input으로 있다는 사실을 알고 있다면, 우리는 random variable들에 대해서 conditional independence를 확인해 볼 수 있다. 만약 $X$에 대해서 이미 확인이 된 $Z$가 $Y$로 가는 길을 모두 막고 있다면 conditional independence가 확인이 된 것이다. 만약 모든 path가 $Z$에 의해서 막혀있다면, 이미 확인이 된 $Z$에 대해서 $X$와 $Y$는 서로 conditionally independent하게 된다. 만약 $X$에서 $Y$로 가는 edge가 하나 추가가 된다면, $X$와 $Y$는 서로 conditonally dependent 할 것이다. 이렇게 undirected graph는 매우 흥미롭고 유용하며 설명하는데 있어 직관적이다.

만약 우리가 $X$에 대해서 classifier나 predicter를 만들고 싶지만, 모든 8개의 random variable에 대해서 model을 만들 수 있다고 가정하고 $Z$에 대해서 관찰이 가능하다고 한다면, 이렇게 $Z$가 주어졌을 때 conditional independence를 가지는 것은 conditional independence가 random variable의 수를 줄이는 것을 허락한다. 즉, 우리는 $Z$에 conditionally independent한 $Z$ 오른쪽의 3개의 random variable은 고려할 필요가 없어진다. $Z$를 모른다면 우리는 아마 latent variable $Y$를 학습할 필요가 있다. 하지만 만약 $Z$를 알게 된다면 $Z$ 자체로 충분한 정보를 가지고 있기 때문에 $X$를 예측하기 위한 $Y$에 대해서는 신경 쓸 필요가 없어진다.

이렇게 model로부터 input의 개수를 줄일 수가 있어서 계산이 빨라지고 결과가 좋아질 것이다. 왜냐하면 만약 모든 8개의 random variable에 대해서 model을 만든다고 했을 때 이러한 conditional independence에 대해서 알지 못한다면 model은 $Y$에 쉽게 overfit 될 것이다. 이는 서로 conditoanl independence를 알고 있다면 멍청한 짓이다. 이러한 관점에서 conditional independence는 매우 중요하다. 그래서 이러한 멋진 조건을 우리는 Markov property라고 부른다. Markov라고 하는 것은 latent variable에 대해서 무시할 수 있다는 것이고, 위에서 $Z$를 보면 $Y$쪽은 볼 필요가 없어진다. 어쨌든 $X$와 $Y$는 $Z$에 대해서 conditional independence하기 때문이다. 그래서 $Z$는 멋진 independence를 제공해주고, 이를 Markov property라고 할 수 있다.

Hammersley-Clifford Theorem(1971)

다음은 undirected graph에서의 conditional independence에 대한 형식적인 설명이다.
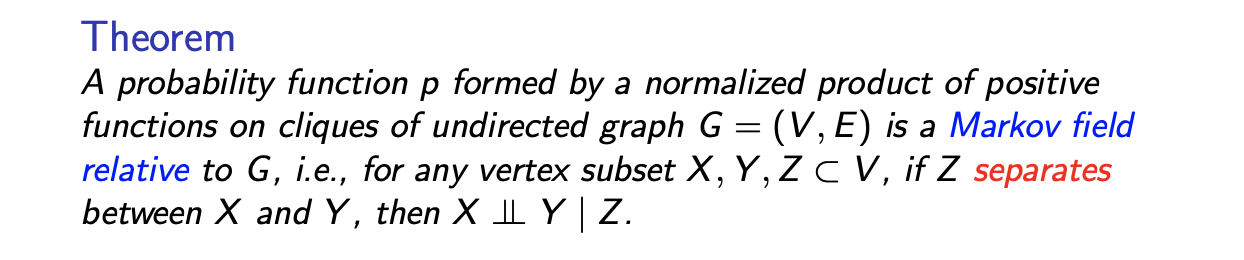Undirected graphical model이 주어졌을 때, Markov field를 $Z$에 의해서 나눠지는 vertex subset $X$, $Y$, $Z$에 대해서 observation $Z$가 주어졌을 때의 $X$, $Y$의 conditional independence로 정의할 수 있다. 이것은 단지 conditional independence의 형식적인 설명일 뿐이다.

Proof of Hammersely-Clifford Theorem

Hammersely-Clifford Theorem의 증명은 conditional independence에 대해서 joint probability가 potential function에 비례한다는 것을 통해서 쉽게 확인할 수 있다. 만약 $X, Y, Z$가 존재하고 $Z$에 대해서 이미 알고 있다면, $XZ$와 $ZY$로 2개의 clique가 존재하게 된다.

이때 joint probability는 각각의 clique에 대한 potential function에 비례할 것이다. 만약 $Z$가 고정이거나 미리 주어졌다면 conditional joint probability를 다음과 같이 적을 수 있다.

결국 이는 $X$와 $Y$가 $Z$에 대해서 conditional independence를 만족하고 있다고 말하는 것이다.

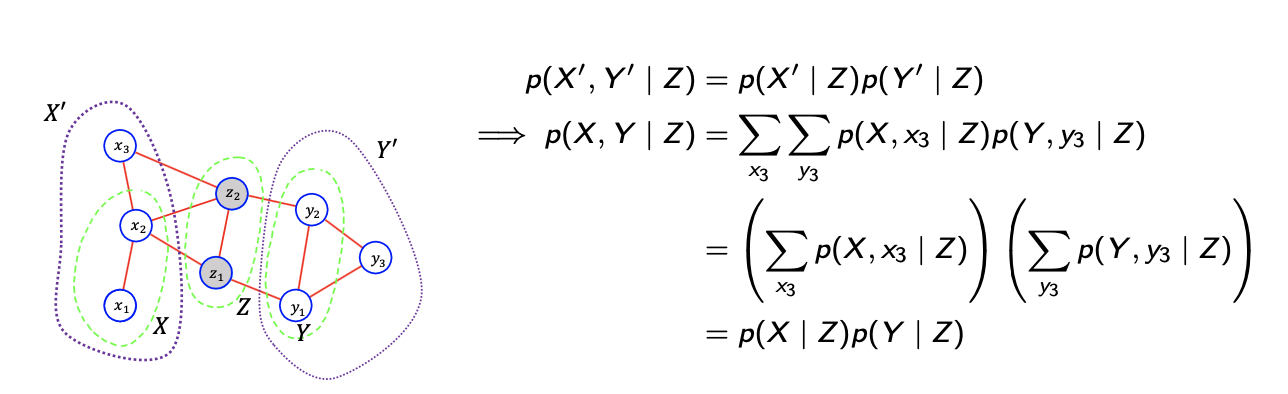그래서 좌측의 topology로부터 $X'$과 $Y'$이 $Z$에 의해서 나누어져 있고, 이는 2개의 cluster에 해당하게 된다. 첫번째 cluster는 random varable $X$에 대해서, 두번째 cluster는 random variable $Y$에 대해서 대응되고 있다. 이로부터 $X'$과 $Y'$의 $Z$에 대한 conditional independence를 확인할 수 있어서 $X'$의 subset인 $X$와 $Y'$의 subset인 $Y$에 대한 conditonal independence도 확인할 수 있다. 위의 식은 가볍게 유도가 되는 것이기 때문에 이러한 과정을 통해서 Hammersley-Clifford Theorem을 증명할 수 있으며, 이러한 과정은 다음의 설명으로 좀 더 일반화 할 수 있다.
이는 단지 위의 유도하는 과정에서 있는 식을 좀 더 일반화하여 나타낸 것일 뿐이다.

Markov Property in Directed Graph

이번에는 directed graphical model에 대해서 conditional independence를 보도록 하자. 여기서는 conditonal indepence를 설명하기 위해서는 좀 더 복잡한 기준이 필요하게 된다. Undirected graph에서는 topology를 간단하게 해서 conditional independence를 정의할 수 있었다. 그러나 directed graph에서는 conditional independence를 확인하기 위해서 3개의 sub topology가 필요하다. 모든 topology에서 head와 tail은 condition의 perspective에 의해서 정의된다.
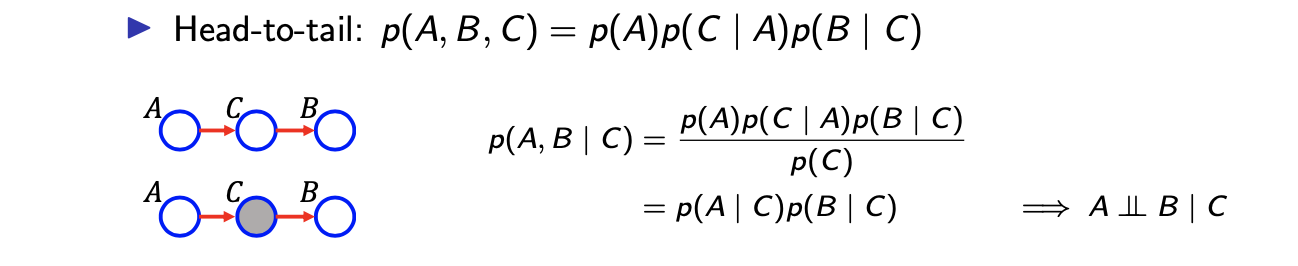첫번째는 head-to-tail topology이다. 여기서는 $C$가 condition이고, $C$가 $A$의 head이자 동시에 $B$의 tail이 된다. 이러한 형태를 head-to-tail이라 부른다. 이러한 조건이 충족되면 $C$에 대해서 $A$와 $B$가 conditional independence를 만족하게 된다. 이에 대한 증명은 정의로부터 쉽게 확인할 수 있다. Directed graphical model의 정의로부터 $P(A,B,C) = p(A)\,p(C|A)\,p(B|C)$가 된다. Conditional probability 정의에 의해서 joint probability를 $C$에 대한 marginal probability로 나눠주게 된다. 그러면 결국 $\frac{p(A)\,p(C|A)}{p(C)}=p(A|C)$이기 때문에 conditional independence를 정의할 수 있게 된다.

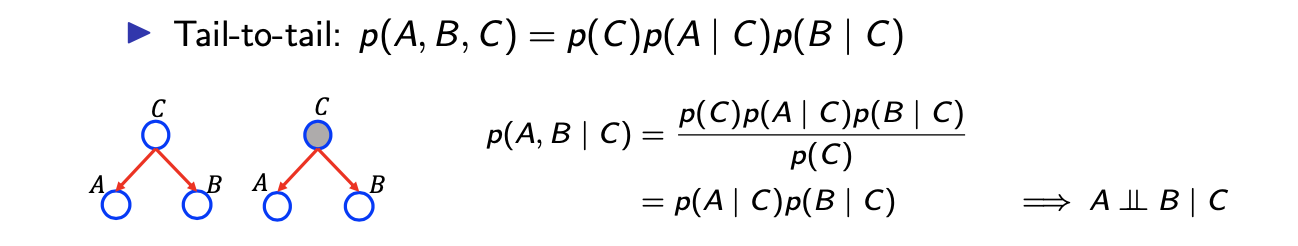두번째는 tail-to-tail topology이다. 이름에서부터 $C$가 나머지에 대해서 tail이 되면 되고, 이는 나머지에 대해서 parent node가 되는 셈이다. 이러면 $P(A,B,C) = p(C)\,p(A|C)\,p(B|C)$가 되고, head-to-tail과 같은 맥락으로 분석을 하게되면 또 다른 conditional independence를 확인할 수 있다.

세번째는 head-to-head topology이며 꽤 중요하다. 여기서는 condtional independence를 보여주기 보다는 marginal independence를 보여주게 된다.

Head-to-head인 경우에 대해서 우리가 말할 수 있는 것은 $A$와 $B$가 marginal independence라는 것이다. $A$와 $B$가 independent한 것은 오직 $C$에 대해서 알지 못할 때고, 이는 매우 중요한 사실이다. 만약, $C$에 대해서 알고 있다면 $A$와 $B$ 사이의 dependence를 예상할 수 있다. 더불어 head-to-head는 또한 확장해서 적용이 가능하다. 위의 예시에서 3번째 graph를 보면 $D$가 추가되어 있다. 이를 보고 $A$와 $B$가 marginal independence하다고 말하고 싶을지도 모른다. 그러나 이는 $D$를 알게 된 이후에는 사실이 될 수 없다. 예전에 예시를 통해서 만약에 스프링쿨러를 동작시키는 것과 비가 오는 것이 우리가 땅이 젖었다는 것을 모른다면 서로 independent하게 된다. 하지만 우리가 땅이 젖은 것을 보게 된다면, 스프링쿨러와 비는 더이상 independent하지 않고 이들 사이의 상관 관계가 생기게 된다. 만약 땅이 젖었다는 사실을 알게 된다면 스프링쿨러와 비의 확률은 아마 증가할지도 모른다. 그러므로 이는 스프링쿨러와 비 사이의 dependence를 설명하게 되고, 우리의 이러한 관찰 속에서 이들 사이의 independence를 설명하는 것은 불가능할지도 모른다.

D-Separation

Undirected graph에서 random variable 두 부분에 대해서 conditional independence를 만드는 것은 쉬웠다. 이로부터 두 부분을 conditional independent하게 만들기 위해서 어느 random varable이 관찰되어야 하는지 쉽게 결정할 수 있었다. 그래서 우리는 한 부분을 추정하기 위해서 다른 부분을 쉽게 배제할 수 있었다.

그러나 directed graph에서는 head-to-head topology가 더이상 간단한 일이 아니며 좀 더 복잡해졌다. Directed graph에서 conditional independence를 확인하기 위해서 다음의 과정을 거쳐야한다.
Directed graph에서 edge 방향을 무시하는 path를 정의해보자.
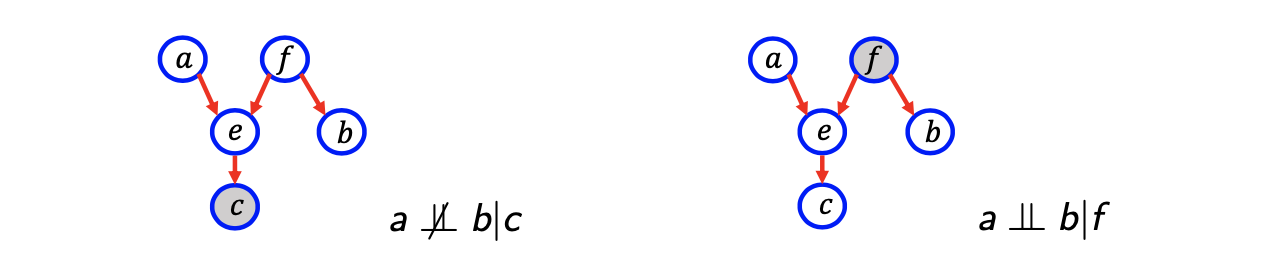좌측의 예시에서 a에서 b로 가는 path가 있다고 가정할 것이다. 이때, 화살표의 방향은 무시한다는 의미이다. 그래서 f에서 e로 화살표는 되어 있지만, 반대 방향으로 가정하려고 한다. 그래서 이러한 path를 정의하고 $C$가 주어졌을 때 $A$와 $B$가 conditional independence하다고 말하는 것은 모든 path가 $C$에 의해서 block 되었을 때를 말한다. Directed graph에서 block이라는 것은 위의 과정에서 존재하는 2가지 경우 중 하나를 해당하면 된다.

첫번째 경우는 매우 간단하다. Head-to-tail이나 tail-to-tail에 대해서 확인만 하면 된다. 위의 우측 예시에서 a와 b는 하나의 path만이 존재하고 f가 이 path에 포함이 되게 된다. 이러한 과정에서 f는 e와 b로 방향이 되어 있기 때문에 tail-to-tail topology에 해당하게 된다. 그래서 우리는 이 path가 observation f에 의해서 block 되어 있다고 말할 수 있다. 그리고 blocked path라는 것은 두번째 경우에 대해서도 생각해봐야 한다. 두번째 경우는 negative sentence로 다소 혼란스러울 수 있다. 설명을 해보면 아마 head-to-head topology에서는 $C$나 $C$의 자손들이 필요 없을지도 모른다. 다시 좌측의 예시를 보면 a부터 b까지의 path가 있을 것이다. 여기서 a, e, f에는 head-to-head topology가 포함되어 있고, e는 c의 선조가 된다. 이는 e의 자손은 c가 되어 이 역시 head-to-head topology에 해당한다. 그래서 우리는 c에 의해서 path가 block 되었다고 이야기하지 않을 것이다. 그래서 c가 주어졌을 때 a와 b 사이에는 상관 관계가 존재하게 되고, conditional independence를 말할 수 없을 것이다. 결국 directed graph에서 conditional independence는 위와 같이 복잡하게 정의가 되어지지만, 이러한 식으로 conditional independence를 정의하는 기준을 세울 수 있다.

사실 marginal independence도 이러한 성질들을 바탕으로 쉽게 찾을 수가 있다. 원하는 variable 사이의 모든 path를 방향과 상관없이 고려했을 때, 모든 path가 independent한 조건을 만족하면 marginal independence를 만족하게 되는 것이다. 여기서 각 path에 있는 variable들 사이의 관계를 봤을 때 head-to-head의 경우가 존재하는 경우에는 해당 path가 independence를 만족하게 되는 것이고, 모든 path에 대해서 이 조건을 만족하면 결과적으로 marginal independence를 만족하게 된다.

Markov Blankets

Conditional independence를 만들기 위해서 어떠한 random variable이 observed 되어야 하는지는 굉장히 중요하다. 우리가 1개의 random variable을 conditional independence를 만들고자 할 때 이 random variable과 연결된 random variable들을 Markov blanket이라고 한다. 그리고 Markov blanket의 크기가 작다면, 이를 Markov boundary라 한다. 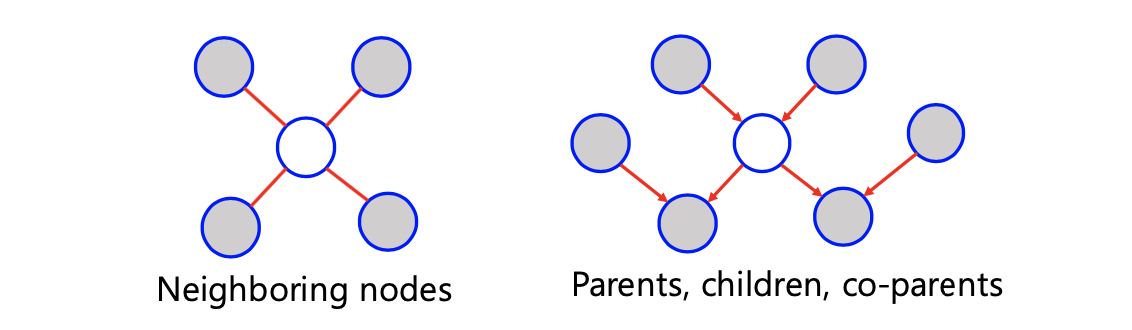중심의 하얀 노드를 a, 나머지 회색 노드를 통틀어서 c라고 할 것이고, 이 밖에 가상의 노드들이 존재한다고 하고 이를 b라고 할 것이다. Undirected graph에서는 명쾌하게 연결되어 있는 이웃하는 random variable을 말하며, directed graph에서는 연결되어 있는 부모, 자식, 그리고 자식의 부모까지 모두를 포함해서 말하게 된다.

이러한 개념이 machine learning에서 매우 영감적인 접근법을 제공해주게 된다. 하나의 random variable에 대해서 평가하기 위해서 다른 random variable에 대해서 marginalization이 필요할지도 모른다. 그러나 marginalization이 exponential computation이 필요하기 때문에 문제가 된다. 그래서 이러한 문제를 피하기 위해서 목표로 하는 random variable(a)이 아닌 이 random varaible과 나머지 random variable(b) 사이의 conditional independence를 만드는 Markov boundary(c)를 보기로 했다.

Explaining Away

그래서 조금은 어려운 Markov boundary라는 개념과 더불어 directed graph에서 head-to-head topology는 매우 난해한 문제이다. 하지만 head-to-head라는 것이 undirected graph보다 directed graph를 사용하는 가장 주된 이유가 되기도 한다.
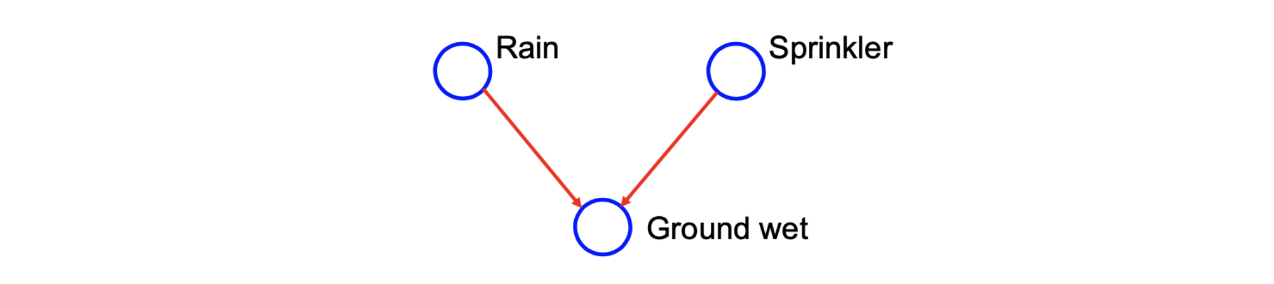위의 diretecd graph를 통해서 비와 스프링쿨러가 marginal independent하다고 말할 수 있다. 그러나 자식인 젖은 땅을 통해서 conditional independent하다고 말할 수도 있다.

그러나 이러한 head-to-head 관계는 undirected graph에서는 사용되지 않는다. 이러한 이유 때문에 directed graph를 사용하는 것이고, 이렇게 directed graph에서만 설명이 가능한 것을 explaining away라고 한다.

Undirected vs. Directed

이와 유사하게 undirected graph에서만 사용이 되는 표현이 존재한다. Directed graphical model에서는 cycle을 가지는 것을 허락하지 않는다. 그래서 다음과 같은 topology는 사용이 불가능하다.
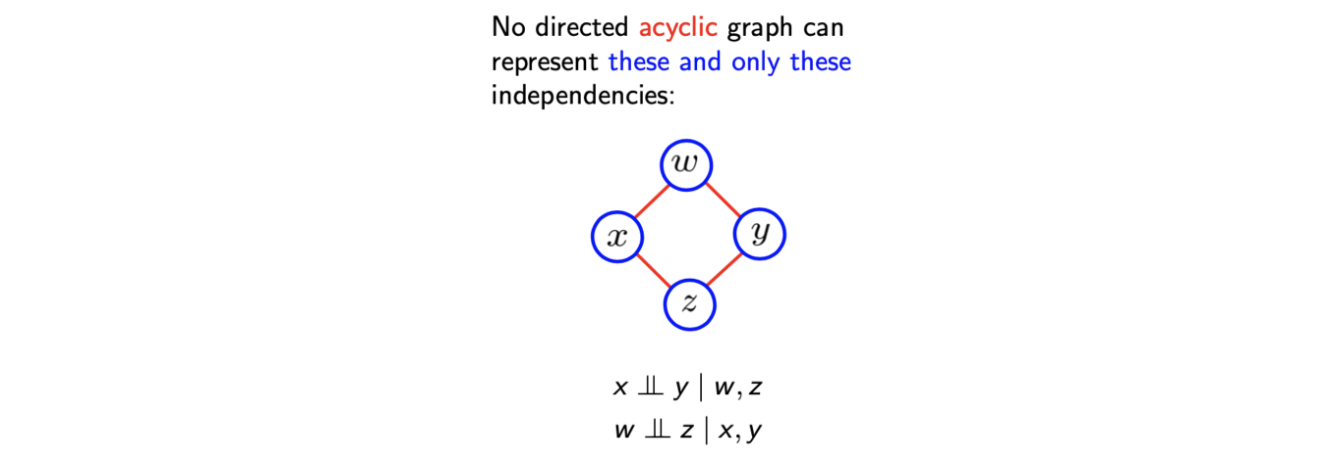위와 같은 conditional independence가 directed graph에서는 절대로 사용할 수 없다.
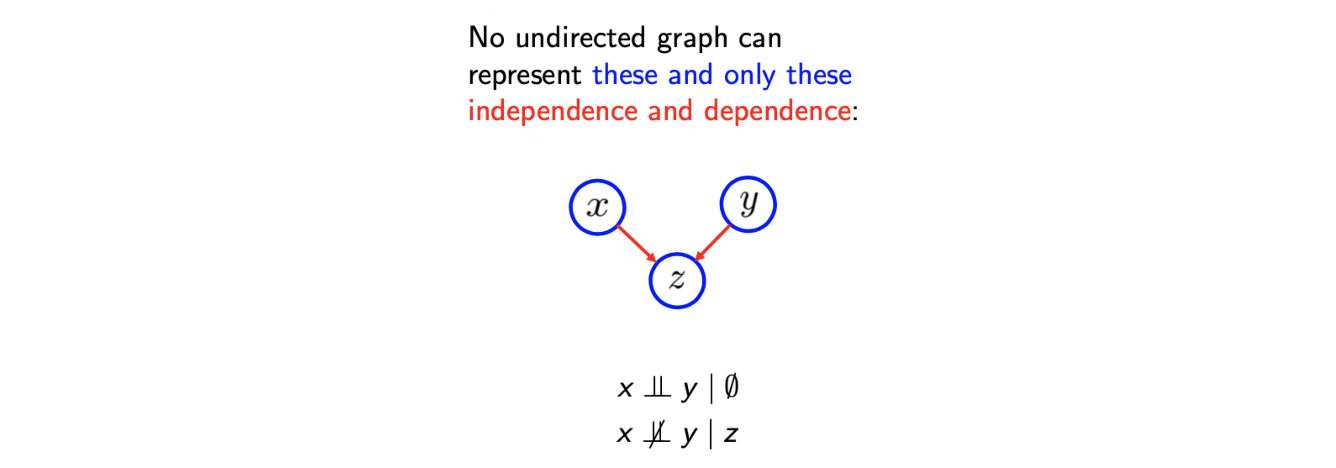Directed graphical model에서는 explaining away에서 이야기 했듯이 marginal independence와 conditional dependence가 undirected graph에서는 사용할 수 없다. 이는 undirected graph와 directed graph 사이의 일종의 trade-off이다.

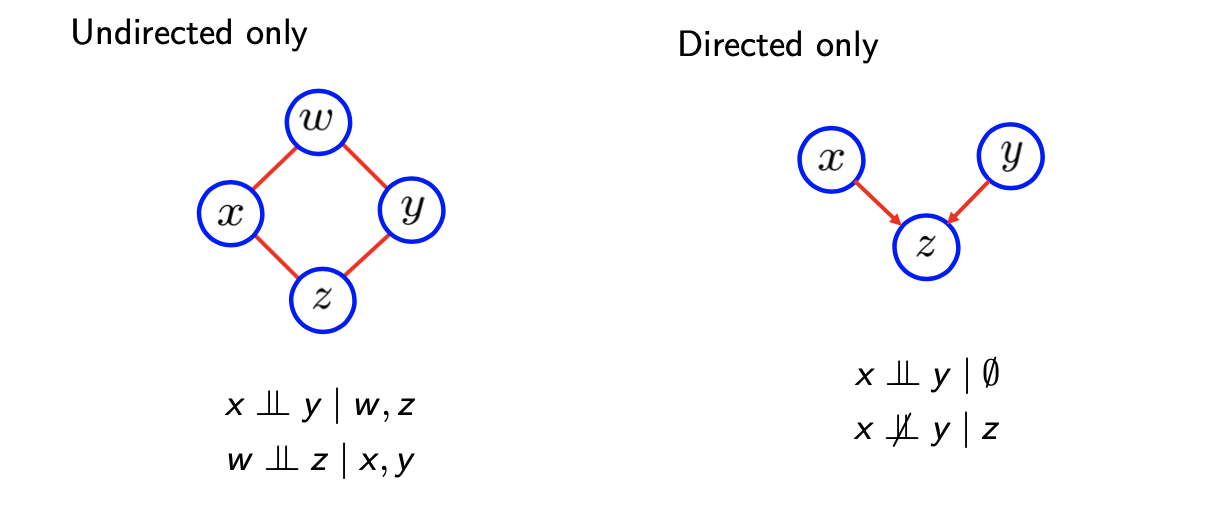그래서 graphical model을 그리는 하나의 접근법을 만들기 위해서 가장 일반적인 관계를 찾으려고 했고, 이를 위해서 하나의 해석에 대해서 이야기해보고자 한다. Graphical model은 joint probability의 factorization의 시각화일 뿐이다.

Directed graph에서는 conditional probability에 대한 factorization이고, undirected graph에서는 maximal clique에 대한 factorization이다.

이로부터 더 일반적인 graphcial model을 factorization을 표현하기 위한 방법으로 생각할 수 있고, 이는 다음에 볼 factor graph에 대한 것이다.

Factor Graph

Factor graph는 본질적으로는 random variable과 factor 사이의 bipartite graph이다. Factor graph는 모든 factor들의 곱에 의해서 joint probability를 factorization 하는 것이다.

여기서 factor는 neighboring random variable의 function이다.
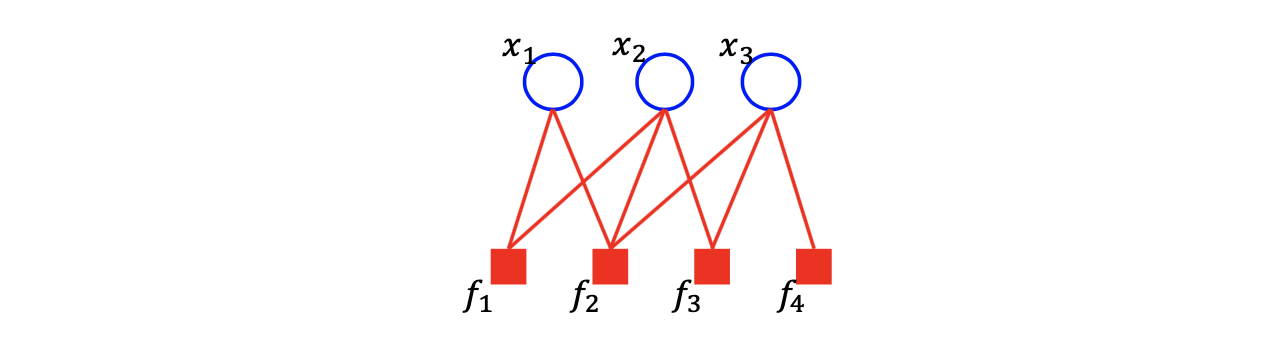위의 예시와 같이 bipartite graph 혹은 factor graph가 주어졌을 때, 대응되는 joint probability는 다음과 같이 나타낼 수 있다.

Joint probability는 각각의 factor의 곱으로 이루어지게 되며, 각각의 factor는 neighboring random variable들을 input으로 가지고 있다. $f_1$의 경우는 neighboring random variable로 $x_1, x_2$를 가지게 되어 $f_1(x_1,x_2)$가 되는 것이다. 다른 factor들도 정의에 따라 정해지게 된다. 그래서 factor graph가 주어지면 이를 joint probability의 factorization form으로 바꿀 수가 있다. 물론, 반대로 joint probability가 factorization form으로 주어졌을 때, factor graph를 그릴 수 있다.

Conditional Independence in Factor Graph

이번에도 Markov blanket을 정의하거나 우리의 model을 최소화하기 위해서 등의 이유로 factor graph에서의 conditional independence를 확인해 볼 것이다. 그래서 z에 대해서 x와 y의 conditional independence를 알아보기 위해서 x에서 y로의 모든 path를 확인하고, 모든 path가 z에 의해서 block 되어 있는지 확인할 것이다. 이는 undirected graph에서 blocked path와 개념적으로는 같은 내용이다. 다음의 예시를 보자.
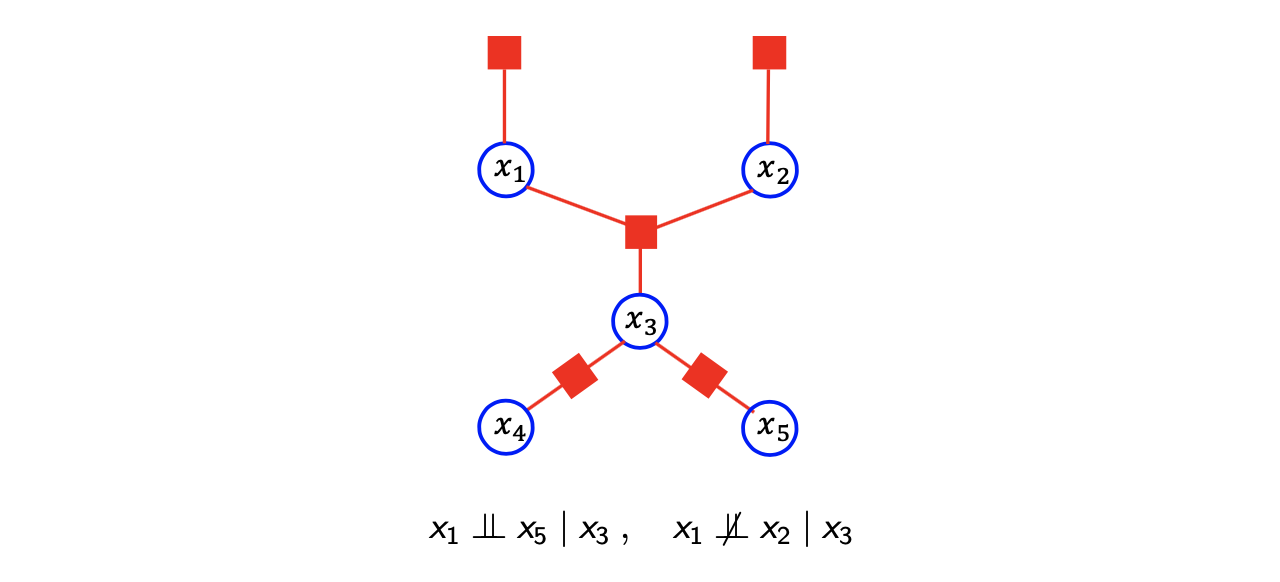$x_1$과 $x_5$를 잇는 path를 보면 $x_3$에 의해서 block 되어 있다. 그래서 $x_1$과 $x_5$는 $x_3$에 대해서 conditional independence를 만족하게 된다.

이번에는 $x_1$과 $x_2$를 보도록 하자. $x_1$과 $x_2$를 잇는 path를 보면 $x_3$에 의해서 block 되어 있지 않다. 이를 통해서 $x_1$과 $x_2$는 어떠한 dependence를 가지게 됨을 쉽게 확인할 수 있다. 이렇게 factor graph에서 conditional independence를 확인해보았다.

Factor Graph Specialized for Factorization

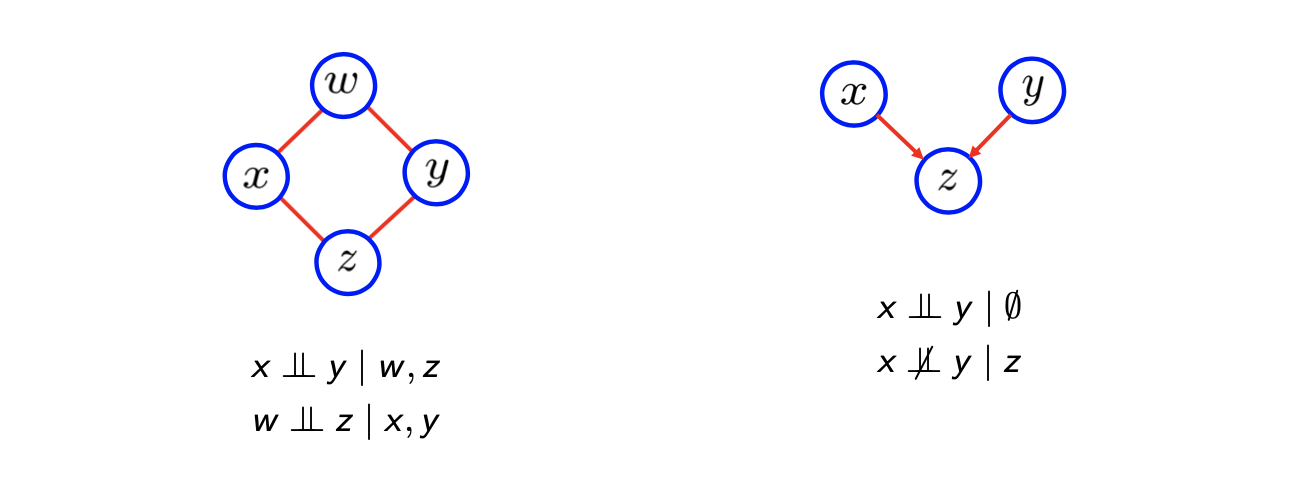지금껏 보았던 이러한 예시는 undirected graph와 directed graph 모두에서 중요한 내용을 가지고 있으며, 이들은 factor graph로 표현이 가능하다. 그래서 factor graph는 양쪽 모두에 대해서 일반적인 표현이 가능하게 된다.

Marginal independence는 graph에서는 확인이 불가능하다. 다음의 예시를 보도록 하자.
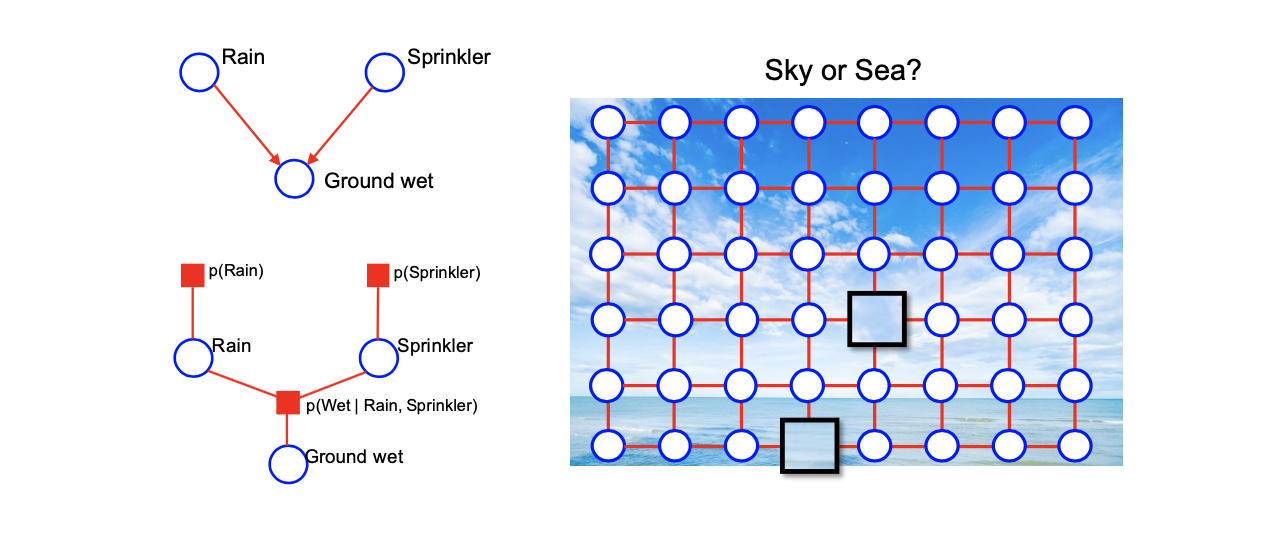물론, 우리는 marginal independence 표현할 수 있지만, factor를 조심스럽게 정의하지 않으면 marginal independence는 graph적인 관점으로는 바로 발견되지 않는다. 위의 directed graph에 대응되는 factor graph를 보면, directed graph에서는 graph의 관점에서 marginal independence를 쉽게 확인이 가능하지만, factor graph에서는 graph의 구조만을 보고서 우리가 marginal independence를 함부로 이야기할 수 없다. Factor graph가 주어졌을 때 directed graph에서 동일한 factorization을 표현할 수 있지만, 이것이 graph를 보는 것 만으로 marginal independence를 확인할 수 있다고 말하지는 않는다. Factor graph에서의 표현의 힘은 매우 강력하고 이는 joint probability의 모든 factorization을 표현할 수 있다.

그래서 우리는 단지 factor graph를 보는 것만으로는 marginal independence와 모든 conditional independence를 확인할 수 없다. 그래서 factor graph를 정의하고 그리기 위해서는 joint probability를 factorization form으로 표현할 필요가 있다. 그러면 이로부터 factor graph를 그려낼 수 있다. 그러나 모든 factorization을 가장 구체적인 단계로 완전히 표현하기 위해서는 여러개를 하나로 묶지말고 하나하나 그리면 된다.

결론적으로 이야기하고 싶은 내용은 joint probability를 potential로 표현하는 것은 가능하다. 그러나 우리는 undirected graph에서 더 디테일한 수준으로는 표현할 수 없다. Undirected graph에서는 joint probability를 여러개의 factorization form으로 표현할 수가 없다. 그러나 factor graph에서 비록 marginal independence를 표현할 수는 없을지라도 joint probability를 여러개의 factorization form으로 표현하는 것이 가능하다.

그래서 graphical model을 그리는 주된 이유는 factorized joint distribution을 표현할 수 있기 때문이다. 그리고 지금까지 factorization이 machint learning tast에서 왜 중요한지에 대해서 알아보았다. Undirected graph와 directed graph에서는 서로의 factorization을 표현할 수 없는 반면에 factor graph는 factorized joint distribution에 특화되어 있고, 모든 factorization을 표현할 수 있다. 즉, factor graph에서는 어떠한 factorization이든 joint distribution이 표현될 수 있다.