[기계학습] Graphical Model - Visualization of Statistical Models 1

Statistical Graphical Model

Graphical model을 공부하기 위한 동기를 부여하기 위해서 statical model을 다시 보려고 한다. Statistical model은 sample data의 생성에 대해서 설명하고 이해하기 위한 일종의 가정들을 말한다. 예를 들어, regression task에서는 $y=w^Tx+\epsilon$ 이라는 generative model에 대해서 다뤘다. 이 model은 어떠한 noise와 더불어 w와 x가 input으로 주어졌을 때, ouput으로 y를 만들어 낸다. 이러한 간단한 식이 일종의 가정, 혹은 model이 되는 것이다. 이러한 식을 바탕으로 우리는 random variable들 사이의 dependence들을 쉽게 찾을 수 있다. 식에서 우리는 y와 $\epsilon$이 서로 dependent하다는 것을 알고 있다. 이 둘은 서로 independent하지 않다. 그래서 model로부터 우리는 이러한 dependence들을 찾고 싶은 것이다.

Graphical model은 이렇게 식을 적어서 나타내지는 않는다. 대신에 graphical model에서는 이러한 dependence들을 효과적이고 직관적으로 visualization한다. 일단 구체적인 statistical model을 위해서 graphical model을 그리게 되면, 우리가 할 수 있는 것은 sum-product나 max-product belief propagation 등과 같은 graph 기반의 어떠한 알고리즘을 적용하는 것이다. 자세한 내용은 조금 있다가 다뤄볼 것이다.

Dependence 1: Correlation

Dependence는 구체적이라기 보다는 추상적인 개념에 가깝다. 대부분의 상황에서 일반적으로 dependence는 correlation이나 casuality로 이해될 수 있다. 이 중에서 먼저 correlation에 대해서 알아보려고 한다. Multivariate Gaussian variable에서 다루었던 내용으로 $N(\mu,\sum)$으로 표기할 수 있다. $\mu$는 mean vector이고, $\sum$는 covariance matrix이며, covariance matrix의 원소는 2개의 random variable에 대해서 서로에 대한 covariance를 나타낸 것이다.

이렇게 correlation은 spectrum이 큰 데이터셋으로부터 쉽게 볼 수 있다. 구체적으로 만약 이미지 데이터셋을 생각했을 때, 2개의 grid로 픽셀의 분포를 볼 수가 있다.
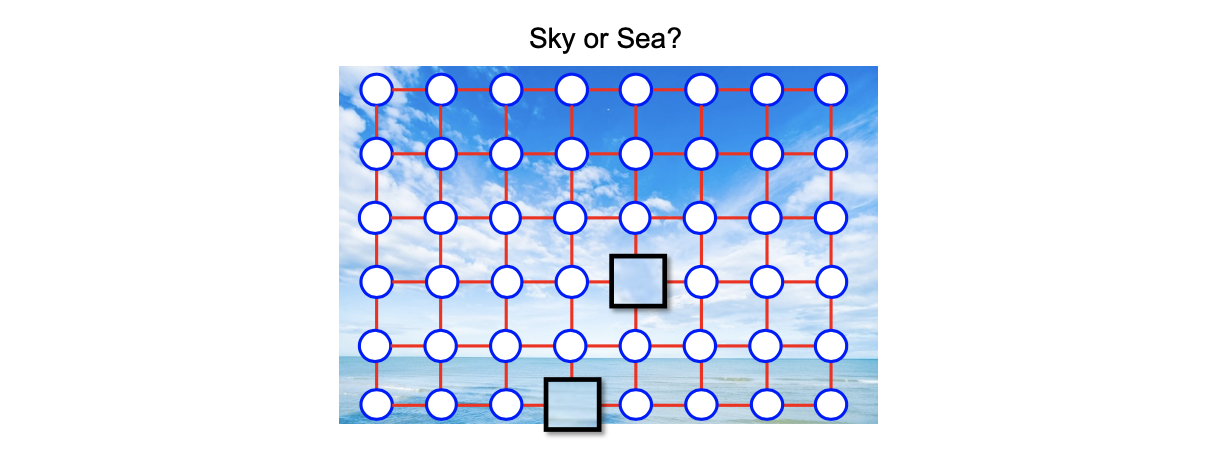여기에서 이웃하는 픽셀들 사이의 어떠한 correlation들이 존재하게 된다. 이러한 이유로부터 convolutional neural network를 image 데이터에 대해서 사용하게 되는 것이다. 이러한 correlation은 데이터를 정교하게 하도록 undirected graph에 의해서 표현된다. 여기서는 dependence에 대해서 구체적인 방향이 존재하지 않는다. 만약 위의 이미지에서 중간에 동그라미로 표현된 픽셀 4개가 graph 상에서 이웃하고 있다면, 이에 대해서 correlation이 있다고 생각하면 된다. 이렇게 correlation을 생각하는 것은 매우 중요하다. 왜냐하면 우리가 만약 해당하는 픽셀이 하늘인지 바다인지를 구별하는 classifier를 build하고 싶고 image 데이터가 완전히 존재한다고 하면, 우리는 쉽게 위쪽은 하늘이고 아래쪽은 바다로 구분할 수 있을 것이다.

그러나 만약 correlation을 무시하고 위의 image에서 네모로 표현된 일부분의 patch만이 주어진다면, 우리는 해당하는 patch가 바다인지 하늘인지는 전혀 알지 못할 것이다. 그래서 정확하게 구분하고 알기 위해서는 데이터들간 correlation을 이해하는 것이 굉장히 중요하다.

Dependence 2: Casuality

다른 종류의 dependence로는 casuality가 있다. Casuality는 어떻게 random variable이 왔는지에 대해서 설명한다. 예를 들어서 우리가 논리를 따지기를 원한다면, 모든 random variable들에 대해서 다음과 같이 생각해 볼 수 있다.
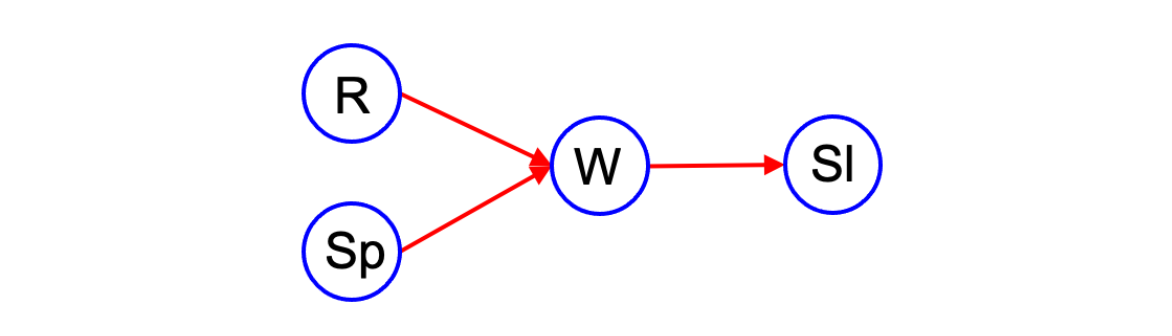R은 rain, Sp는 sprinkler, W는 wet, Sl은 slipped라고 했을 때, 젖은 땅에 대해서는 비나 스프링쿨러를 원인으로 생각할 수 있다. 그래서 R과 Sp에서 W로 향하는 그래프를 그릴 수 있다. 그리고 땅이 젖어있는지 젖어있지 않은지에 대해서 알고 있다면 우리는 왜 미끄러졌는지 추론해볼 수 있다. 이렇게 4개의 random variable에 대한 모든 dependence는 위와 같이 directed graph로 나타낼 수 있다. 이러한 방식은 random varibale들 사이의 casuality를 설명할 수 있다.

Visualization of Statistical Models

그래서 이제부터는 directed model과 undirected model에 대해서 좀 더 형식적으로 알아보고 conditional independence의 notion에 대해서 알아보고자 한다. Conditional independence는 directed graph와 undirected graph 모두에서 쉽게 볼 수 있다. 그 다음으로는 "factor graph"라 불리는 statistical graphical model의 일반적인 형태를 볼 것이다.

Directed Graphical Model(a.k.a. Bayesian Network)

가장 먼저 Bayesian network라고도 불리는 directed graphical model로 directed acyclic graph(DAG)에 대해서 알아보려고 한다. Directed graphical model에서 directed라는 것은 edge가 방향이 존재한다는 것이다. Acyclic이라는 것은 cycle이 존재하지 않는다는 의미로, 방향을 따라서 edge들을 이동할 때, 계속해서 이동하지 못한다. 만약 acyclic graph를 가지게 된다면, 우리는 random variable 사이의 causal relation을 적을 수 있을 것이다.

DAG는 모든 random variable에 대해서 joint distribution을 나타내게 된다. 우리는 random variable에 대해서 각각의 node를 대응시키고, casuality에 대해서는 각각의 edge로 설명하고 싶다. 그러면 이렇게 DAG가 주어지게 되면 모든 random variable에 대한 joint probability를 위와 같은 형태로 나타낼 것이다. $x_i$의 parent가 주어졌을 때 $p(x_i\;|\;\text{pa}(x_i))$는 conditional probability이고, graph에 주어진 모든 node에 대해서 곱으로 나타낼 것이다. 다음의 간단한 acyclic graph를 보도록 하자.
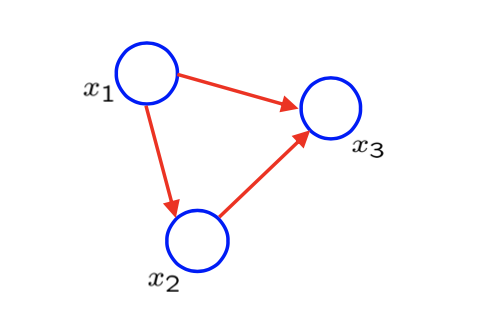그래서 위에서 정의한 것에 의해서 DAG가 주어졌을 때, joint probability는 다음과 같이 분해할 수 있다.

그리고 $p(x_1)$은 $p(x_1|\text{pa}(x_1))$이고, $p(x_2|x_1)$는 $p(x_2|\text{pa}(x_2))$이며, $p(x_3|x_1,x_2)$는 $p(x_3|\text{pa}(x_3))$이다. 여기서 $\text{pa}(x_1)$는 root이며 ancestor, 즉 incoming edge가 없기 때문에 $\varnothing$이다. 그래서 첫번째 항은 $x_1$의 marginality에 의해서 $p(x_1)$이 된다. 반면, $x_2$는 $x_1$이라는 하나의 parent를 가지고 있다. 마찬가지로 $x_3$는 $x_1$과 $x_2$를 parent로 가지고 있다. 그래서 이들은 conditional probability로 적어주면 된다. 이렇게 DAG를 그리게 되었을 때, 자동적으로 joint distribution의 곱셈 형태로 나타낼 수 있다. 반대로 이렇게 곱셈 형태로 주어졌을 때, DAG를 그릴 수가 있다.

Factorization in Directed Graphs

다음은 좀 더 복잡한 directed graphical model이다.
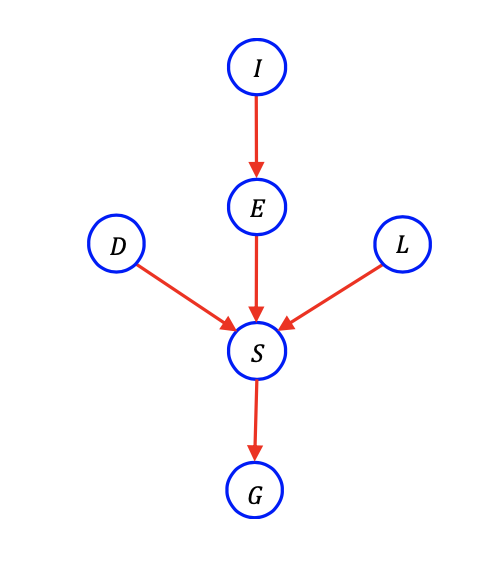예를 들어서 이 model은 어떻게 학생이 성적을 받는지에 대한 설명을 할 수가 있다. 그 과정을 잘 생각해보면 위와 같은 casuality model로 그릴 수가 있다. 학생의 grade(G)는 lecture quality(L), difficulty(D), intelligence(I), efforts(E), score(S)에 dependence를 가지게 된다. 이렇게 총 6개의 random variable들이 위와 같은 casuality를 가질 것이다. 학생의 지성은 얼마나 노력을 해야할지를 결정해주고, 강의의 수준과 어려움 그리고 본인의 노력을 기반으로 점수가 결정이 될 것이다. 점수가 결정이 되면 최종적으로 성적이 결정될 것이다. 이러한 흐름대로 graphcal model을 나타내게 되면 다시 factorized joint probability로 바꿔서 표현할 수 있다.

그래서 directed graph는 많은 수의 random variable이 존재할 때 매우 유용하다. Graphical model을 사용하지 않을 때 6개의 random variable이 있다면 적어도 63($2^6-1$)의 table 크기가 필요하게 된다. 여기서 1을 빼는 이유는 모든 probability의 합이 1이 되기 때문에 1로부터 나머지를 빼주면 구할 수가 있다. 그래서 우리는 마지막 entry는 생략할 것이기에 필요하지 않는다. 만약 factorization을 알고 있다면 joint probability는 factorization form으로 분해될 수 있어서 우리는 굳이 모든 entry를 저장할 필요가 없고 각각의 probability에 대해서 table을 가질 필요가 없다. 즉, factorization을 알게 되면 table의 크기는 63에서 15(1+1+1+2+8+2)로 줄어들 것이다. 앞의 3개의 1은 앞의 3개의 marginal probability를 의미하고 2는 하나의 parent, 8은 3개의 parent를 가지는 conditioanl probability를 의미한다.

여기서 궁금한 부분은 어떻게 1, 2, 8과 같은 숫자를 얻은 것일까? 우선 1은 명확하다. Probability의 합은 1이어야하고, marginal probability는 오직 1개의 parameter를 필요로 한다. 왜냐하면 여기서는 binary random variable이기 때문이다. 다음으로 parent가 하나인 conditional probability는 binary random variable이기 때문에 2개의 parameter를 필요로 한다. 예를 들어 $P(E|I)$는 $P(E|I=0)$와 $P(E|I=1)$로 나뉘어 각각은 1개의 parameter를 필요로 한다. 그래서 총 2개가 되는 것이다. 그래서 이와 유사하게 parent가 3개인 경우에는 총 8개의 paramter를 필요로 하게 되는 것이다. 결과적으로 factorization을 통해서 우리는 joint probability를 나타내는 table의 크기를 줄일 수가 있다. 이는 random variable의 개수가 늘어나면 늘어날수록 더 큰 효과를 보여줄 것이다.

지금 간단하게 binary random variable에 대해서 알아보았지만, 만약 categorical random variable이 되어 여러개의 support가 있다고 해도 table의 크기를 구하는 것은 비슷하다. Binary의 경우 2의 random variable의 숫자만큼 제곱하고 1을 빼주었지만, support가 많아져서 예를 들어 0부터 4까지 5개의 경우가 있다고 하면 5의 random variable의 숫자 제곱에다가 1을 빼주면 그 값이 table의 크기가 될 것이다.

Undirected Graph(a.k.a. Markov Random Field)

Undirected graph가 주어졌을 때 directed graph와 비슷하게 우리는 대응되는 joint probability를 factorized form으로 나타낼 수 있다. 그래서 undirected graph가 주어지면 joint probability를 각각의 maximal clique에 대해서 곱으로 나타낼 수 있다.

Undirected graphical model을 이해하기 위해서 먼저 maximal clique가 무엇인지 알고가야 한다. Clique에 대해서 안다고 하면 clique potential function $\psi_C(X_C)$도 추가로 알 수가 있다. Clique는 node의 부분집합이고 clique potential은 clique에 있는 random variable의 non-negative function이다. 여기서 $Z$는 normalization constant으로 joint probabiliyt의 합을 1로 맞춰준다.

우리는 joint probability의 합을 최대로 하는 것에 관심이 있어서 사실 Z는 크게 중요한 부분은 아니다.

Example of Cliques

이제 자세하게 clique와 maximal clique이 무엇인지 알아볼 것이다. Clique은 node의 부분 집합으로 서로 완전하게 connected 되어 있다. 다음의 예시를 보자.
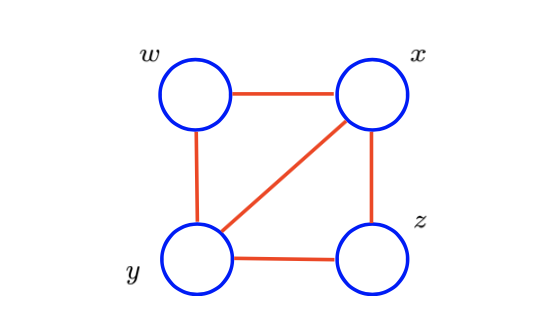여기서 x와 y만 먼저 살펴보면 clique를 형성하고 있다. 이렇게 모든 clique를 살펴보면 wx, wy, yz, xz, xyz, wxy, xy가 된다. 각각의 node들에 대해서 먼저 2개의 node들에 대해서 wx, wy, yz, xz, xy가 이어져 있기 때문에 clique를 형성한다. 그리고 부분 집합으로 3개의 node들에 대해서 xyz, wxy도 완전히 연결되어 있기에 clique를 형성하게 된다. 그렇다면 wy는 왜 maximal clique이 아닐까? 그 이유는 x만을 추가했을 때도 완전히 연결할 수 있기 때문이다.

그러면 이로부터 maximal clique를 이해할 수 있게 된다. Maximal clique는 완전히 connected 되어 있으면서 다른 node들은 포함할 수 없는 clique를 이야기하며, 여기서는 xyz, wxy가 이에 해당된다. 만약 xyz에 대해서 w가 추가가 된다면, w는 x, y와는 연결이 되어 있지만, z와는 연결이 되어있지 않다. wxy에 대해서도 마찬가지로 z가 추가 되었을 때 w와 연결이 되어 있지 않다.

이제 maximal clique가 무엇인지 알게 되었고, 위와 같이 graph가 주어졌을 때 joint probability를 다음과 같이 factorization 할 수 있다.

Z는 normalization factor이고, 2개의 term이 존재한다. 각각의 term은 각각의 maximal clique에 대응된다. Directed graphical model에서는 conditional probability를 그냥 사용했지만, 여기서는 그렇지 않다. Directed graph에서는 사용하지 않은 clique potential function을 undirected graph에서는 사용하고 있다. 이것이 중요한 차이점이 되겠다. 아마 directed graph는 매우 직관적이고 이해하기 쉬웠을 것이다.

Convenient Notation

계속해서 이야기하기 전에 몇가지 편리한 notation을 알아볼까 한다. N개의 random variable의 squence를 가지고 있다고 가정해보자. 그런데 우리는 더 일반적인 경우를 원한다. 그래서 N이 미리 정해지지 않았을 때 우리는 어떻게 이러한 graphical model을 그릴 수 있을까? 다음과 같이 중간에 생략되어 있다는 의미로 dot expression을 생각할 수도 있다.
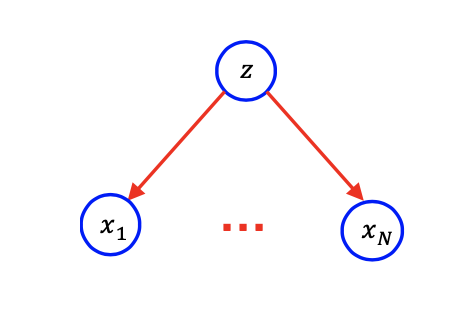하지만 여기서 dot은 애매함을 나타내어 이번에는 다음과 같이 plate notation을 생각할 수도 있다.
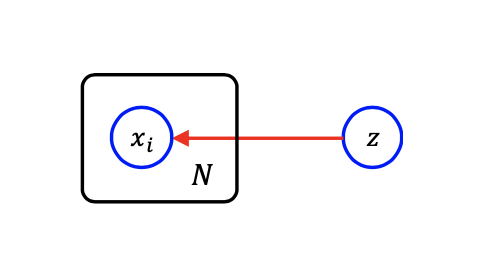만약 1부터 N까지 연속되는 random variable이 다른 random variable과 같은 관계를 가지게 된다면, 위와 같이 간단하게 plate를 그려서 표현할 수 있다. 그러면 대응하는 joint probability는 다음과 같이 표현할 수 있다.

여기서 z는 parent를 가지고 있지 않아 marginal probability가 되고 z에 대해서 conditional probability들의 곱을 계산하여 나타내면 된다.

그리고 하나 더 유용한 notation에 대해서 알아보고자 한다. 우리가 random variable들에 대해서 modeling을 할 때, 종종 partial observability를 가지게 된다. 때때로 우리는 일부분의 random variable을 보게 되고 나머지는 latent가 된다. 이러한 observability를 설명하기 위해서 latent variable을 하얀색의 빈 node로 그리고 observed random variable은 회색의 node로 그리게 된다.
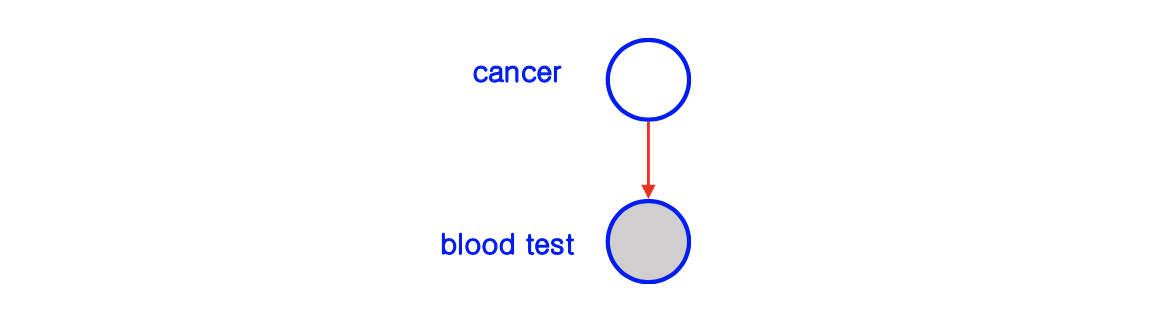이러한 방법은 매우 유용하다. 우리는 누군가가 암에 걸렸다면 그가 blood test를 받아서 암인지 아닌지를 보여준다는 것을 알게 된다. 만약 누군가가 blood test를 받았다면 그가 암인지 아닌지는 latent로 남게 된다. 이는 observable하지 않다. 그래서 위와 같은 graphical model을 그릴 수 있을 것이다.