[기계학습] Some Insights of Model Selection 2

Combining Simple Models

여러 model을 조합해보는 것도 좋은 model을 build하기 위한 또 다른 방법이 될 수 있다. 현실에서는 물리적인 제약들이 많기 때문에 간단한 model들을 조합하는 것도 좋은 방법이 된다. 대표적인 예시로는 AdaBoost, decision tree learning 등이 있고, 이들은 model ensemble의 카테고리에 포함된다.

Model Ensemble

Model ensemble이라는 것은 performance를 향상시키기 위해서 여러개의 model들을 조합하는 방법이다. 사람들은 제각각 다른 인생을 살고 다른 경험을 하며 서로 다른 데이터를 축적하게 된다. 이와 유사하게 model들도 서로 다른 특징들을 가지게 된다. SVM은 하나의 feature에 대해서 진행되기 때문에 하나의 구체적인 feature에 오로지 집중하기 좋다. 반면, MLP는 다른 feature에 대해서 집중할 수 있다. 그리고 ensemble은 다른 model parameter를 선택할 때도 타당하다. 만약 visual tracking system을 만들고 싶을 때, 현실에서 우리는 대부분을 tracking 하지 않는다는 것을 알고 있다. 특정 지점에서 target object가 장애물에 가려지게 된거나 비슷한 object가 다가오고 있다면, 해당 target에 더 집중하려는 경향을 보이게 된다. 그래서 일반적인 상황에 대해서 작은 model을 ensemble하면 inference speed를 올려주고 energy 사용을 줄여 줄 것이다. Model ensemble은 입력으로 사용되는 데이터가 다르게 표현되어 있을 때에도 유용하게 사용이 된다. 만약 병원에 있을 때 MRI, CT, X-ray 등을 이용하게 되는데 이 장비들을 이용하면 서로 다른 결과를 볼 수가 있다. 하나의 장비에서 볼 수 없는 문제를 다른 장비를 통해서 볼 수가 있다. 그래서 이 장비들의 결과를 조합해서 몸에 이상이 있는지 판단하게 된다. 이러한 상황들이 model ensemble적인 측면인 것이다. 결론적으로 학습을 할 때 성능을 높이기 위해서 여러 model들을 함께 사용하게 되면 기존보다 더 높은 성능을 기대할 수 있다.

Adaptive Boosting(AdaBoost)

유명한 model ensemble 기법으로는 adaptive boosting, 줄여서 AdaBoost가 있다. 이 기법은 weak classifier $f_t: \mathcal{X} \mapsto \mathcal{Y}$의 $set \; \mathcal{F}$를 고려한다. AdaBoost에서는 weight가 $\alpha_t$인 weighted majority vote를 가진 weak classifier를 찾기를 원한다.

이렇게 많은 weak classifier로 되어 있는 model에 대한 ensemble을 build하기 위해서 우리는 $\alpha_t$와 $f_t$를 결정할 필요가 있다.

AdaBoost: An Iterative Method

그래서 AdaBoost 알고리즘을 설명하기 위해서 다음 recursion으로부터 시작하려고 한다. $F_T$는 $F_t(x)=\sum_{t'=1}^t \alpha_{t'}f_{t'}(x)$로 일반화 될 수 있다.

$F_t$의 정의로부터 우리는 위의 recursion이 연속적인 $F_t$와 $F_{t-1}$의 차이가 $\alpha_t f_t(x)$임을 알 수가 있다. 그래서 $F_{t-1}$이 주어졌을 때, $F_{t}$를 build하는 것은 $\alpha_t$와 $f_t$를 고르는 것이다. 그렇다면 이는 어떻게 고를 수 있을까?

우선, $F_t$의 error $E(F_t)$에 대해서 정의하려고 한다.

여기서 사용하는 error는 logitstic error이고, 모든 데이터에 대해서 summation을 할 것이다. 그리고 factor $\gamma_t^{(i)}$를 정의하려고 한다.

이제 $F_t$에 대한 recursion과 정의한 error를 이용해서 우리는 $E(F_t)$를 다음과 같이 다시 적을 수가 있다.

그래서 최적의 $f_t$는 가장 작은 error $\sum_{i:y^{(i)}\neq f_t(x^{(i)})} \gamma_t^{(i)}$를 가지는 $f_t$를 고르면 되는 것이다. $e^{\alpha_t} - e^{-\alpha_t}$는 $f_t$를 선택하는데 있어서 일종의 constant이다. Factor인 $\gamma_t^{(i)}$가 $t-1$까지 각각의 error의 일종인 것은 직관적이다. 그러면 우리는 $f_{t-1}$를 만드는 error를 최소화 하기를 원한다. 그래서 $f_t$를 선택하는 것은 이렇게 하면 되고, 이제 남은 것은 $\alpha$ 값을 고르는 것이다. 이를 위해서 우리는 derivative를 계산해서 0이 되는 값을 구할 것이다.

그러면 결과가 다음과 같은 것이다.

Algorithm: AdaBoost for Binary Classification

이를 요약해보면 위의 순서에 따라서 연속적인 $f_t$를 선택하는 것으로 다음과 같이 정리할 수 있다.

General Observations on AdaBoost

지금부터는 AdaBoost에 대해서 좀 더 자세히 이해해보려고 한다. 특히, $\alpha_t$를 선택하는데 있어서 자세히 보고자 한다. $\epsilon_t$는 $f_t$의 error weight로 해석될 수 있다.

$\epsilon_t$가 $1/2$보다 큰 경우는 $f_t$가 제대로 일을 하지 못해서 해서 답을 반대로 낸 경우다. 그래서 $\epsilon_t$가 $1/2$보다 큰 경우에는 $\alpha_t$가 어떠한 negative 값으로 계산이 될 것이다. 그래서 우리가 weighted majority voting을 택하기 때문에 우리는 더 좋은 model을 만들기 위해서 negative $f_t$를 선택해야 한다.

$\epsilon_t$이 0이 되는 경우에는 $\alpha_t$가 infinity($\infty$)가 될 것이고, 이는 $f_t$가 완벽하다는 의미이다. 그래서 우리는 그냥 $f_t$의 선택을 따라가기만 하면 된다.

$\epsilon_t$가 $1/2$인 경우에는 $f_t$가 주는 것이 아무것도 없기 때문에 $\alpha_t$를 그냥 무시하면 된다. 그리고 이는 $alpha_t$가 0이 될 것이다.

누구나 AdaBoost를 이용해서 $f_t$가 매우 작은 ensemble model을 build 할 수 있다. 그러면 energy 소비를 줄일 수 있고 computational cost도 줄일 수 있다.

Decision Tree

여러 model을 ensemble하는 또 다른 방법으로는 decision tree가 있다. Decision tree는 다음과 같이 나타낼 수 있다.
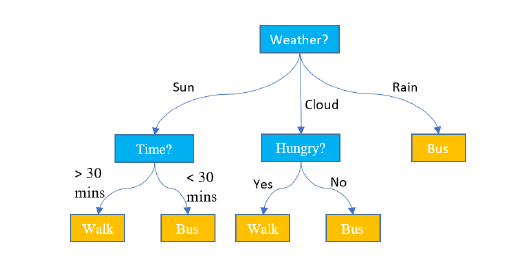이 예시는 편의성을 최대로 하기 위해서 내가 걸어갈지 혹은 버스를 탈지 결정하는 classifier이다. 그래서 걸어갈지 아니면 버스를 탈 지 정하기 위해서 먼저 날씨를 확인해 봐야 한다. 만약 비가 오는 날씨라면, 걸어가지는 않을 것이다. 이러한 경우에는 버스를 타기로 결정할 것이다. 만약 날씨가 맑고 충분한 시간이 있다면, 걸어가도 괜찮을 것이다. 만약 시간이 충분하지 않다면, 맑더라도 버스를 탈 것이다. 추가적으로 만약 날씨가 흐리더라면, 시간 대신에 배고픈지 아닌지 결정에 따라서 걸어가든지 버스를 타든지 할 것이다.

이렇게 사람의 뇌로 쉽게 생각해 볼 수 있는 상황을 decision tree로 나타내 보았다. Decision tree에 있는 각각의 질문들에 대해서 model로 간주할 수 있다. Decision tree에서 아마 model마다 다른 output을 가지게 될 것이다. 그러나 AdaBoost에서는 각각의 f_t에 대해서 -1 혹은 +1을 가지게 된다. Decision tree에서 모든 model이 같은 output을 내지 않아도 된다.

Learning Decision Tree

이러한 이해를 바탕으로, 어떻게 하면 좋은 decision tree를 만들고 학습 시키리 수 있을까? 이를 위해서 Iterative Dichotomiser 3(ID3), Classification and regression tree(CART) 등 많은 알고리즘들이 존재한다.

그러나 보통은 decision tree를 학습하는 알고리즘은 데이터셋을 split하려고 시도하고, leaf node가 하나의 lable을 가지는 데이터를 포함하도록 기대할 것이다. 위의 예시로부터 우리가 기대하는 것은 많은 데이터셋이 있을 때, output으로는 버스를 탈지 아니면 걸어갈지다. Decision tree로부터 데이터셋 $D=\{ x_1^{(i)}, x_2^{(i)}, x_3^{(i)}, y^{(i)}\}$이라 했을 때, 각각의 결정에 대해서 데이터셋을 split하여 $D_1(Walk), D_2(Bus), D_3(Walk), D_4(Bus), D_5(Bus)$라고 해보자. 그러면 이 decision tree로부터 우리가 원하는 것은 각각의 leaf node에 하나의 lable을 대응시키는 것이다. 즉, $D_1$이라는 데이터에 Walk라는 lable을 대응시키는 것이다. 이렇게 모든 데이터셋에 대해서 하나의 lable을 대응시키면 된다.

Metric for Measuring Best Split: Information Gain

그러면 어떻게 더 형식적으로 이러한 decision tree를 나타낼 수 있을까? 이제부터 하나씩 알아보기로 하자. Best split을 위한 metric으로는 다음과 같이 information gain이 있다.

Informatino gain은 데이터셋 $\mathcal{D}$와 split function $f$가 주어졌을 때, 얼마나 많은 information이 데이터셋에 포함되어 있는지에 대한 훌륭한 measure로 $I(\mathcal{D})$와 데이터셋의 split에 의해서 결정이 된다. 다소 이해하기 어려울 수는 있지만, 앞으로 더 자세하게 알아볼 것이다.

그리고 $I(\mathcal{D})$에 대해서는 Gini impurity, Entropy, Classification error 등 여러 candidate가 있다. 이 중에서 entropy에 대해서 집중해보려고 한다. 왜냐하면 이는 machine learning에서 굉장히 즐겁고 흥미로운 직관을 줄 수 있기 때문이다.

Information and Entropy

Information gain과 entropy를 이해하기 위해서 entropy에 대응하는 information function의 정의를 먼저 보도록 할 것이다. Random variable X에 대해서 information $I(X)$는 다음과 같이 정의가 된다.

이 random varible X를 X에 대한 realization의 surprise 혹은 uncertainty로 해석할 수 있다. 왜냐하면 $p(X)$가 매우 작고, log 함수가 증가하는 함수이기 때문에 마이너스가 붙게 되면 information은 증가하게 된다. 그래서 surprise나 uncertainty로 해석이 되는 것은 X의 realization이 덜 일어나게 되면 information이 커지기 때문이다.

그렇다면 사람들이 왜 이것을 information이라고 부르는 것일까? 그 이유는 이러한 event를 관찰함에 따라서 더 알게 되기 때문이다. 만약 동전 던지기에서 앞면의 확률이 0.999이고 뒷면의 확률이 0.001이라는 사실을 알았을 때, 우리는 앞면이 나오는 것이 더 많이 발생할 것이라는 것을 알고 있다. 비록 상황을 직접 보지 않더라도 앞면의 확률이 매우 높기 때문에 우리는 예상할 수 있다. 그래도 어쨌든 뒷면의 확률도 매우 작지만 존재한다. 그렇기에 뒷면이 나오는 것을 관찰하는 것은 더 많은 information을 전달할지도 모른다. 이러한 사실은 매우 흥미롭고 즐거운 event가 되기에 이론적으로 이러한 상황에 대해서 더 많은 surprise를 줄 것이다. 그래서 뒷면을 관찰하는 것이 더 많은 information을 가지게 된다.

그래서 information의 의미에 대해서 이해를 했다면 entropy를 이해하는 것은 그리 어렵지 않다. 왜냐하면 entropy는 그저 information의 expectation이기 때문이다.

Entorpy의 값은 logarithm의 base에 의존한다. Base b는 양수지만 보통 2를 선택하는데, 다르게 선택해도 된다. 그러나 편의성을 위해서 우선은 2로 정해놓고 갈 것이다. Entropy는 information의 expectation인데, 이 entropy가 작다면 random event를 표현하기 위해서 uncertainty가 작아지게 된다. Information theory에 의해서 information과 entropy의 notion이 정해지게 되었다. 그래서 이러한 개념들은 communication system을 배우기 위해서 information theory를 통해서 발전이 되었고, entropy는 X라는 data를 표현하기 위해서 the minimum bits로서 해석이 될 수 있다. The minimum bits는 다음의 예시를 통해서 살펴 볼 것이다.

Example: Horse Race

8마리의 말이 경주를 한다고 가정해보자. 이때 각각의 말이 우승할 확률은 다음과 같다.

우리는 2진법 코드화된 메시지의 sequence를 다른 사람에게 보내서, 이 경주에 대한 sequence의 승자를 알게 하도록 하고싶다. 가장 단순한 방법은 3개의 bit를 이용하는 것이다. 예를 들어 첫번째 말은 000, 두번째 말은 001, 세번재 말은 010 등의 방식으로 하는 것이다. 그러나 이러한 방식은 bit의 길이라는 관점에 대해서는 optimal하지 못하다. 왜냐하면 우리는 이미 5~8번 말이 우승 할 확률이 매우 낮다는 것을 알고 있다. 그래서 어차피 앞의 4개의 코드를 주로 사용할 것이기 때문에 이러한 방식은 절대로 사용하지 않을 것이다. 그래서 사실 첫번째 말이 우승할 확률이 많기 때문에 bit의 길이적인 측면에서 000을 계속 사용하는 것은 불필요하게 된다.

그래서 communication code를 줄이는 방법으로 짧은 bit에 높은 확률을 가지는 말을 대응시키기로 했다. 첫번째 말은 0, 두번째 말은 1, 세번째 말은 10 등과 같이 bit를 할당하게 되면 평균적으로 bit를 줄일 수 있게 된다. 혹은 우승 확률이 일정하지 않기 때문에 message의 길이를 줄이기 위해서 다음과 같이 더 효과적으로 code를 부여할 수 있다.

이렇게 하면 평균적인 code의 길이가 3 bits에서 2 bits로 줄어들게 된다. 이전에는 $\sum_{i=1}^8 \frac{1}{8}\times 3 = 3 \text{ bits}$ 였는데, 지금은 $\frac{1}{2}\times 1+\frac{1}{4}\times 2+\frac{1}{8}\times 3 + \frac{1}{16}\times 4 +\frac{1}{64}\times 6\times 4 = 2 \text{ bits}$가 된다.

구체적으로 이러한 code message는 decodable해야 한다. 만약 첫번째 말이 0, 두번째 말이 1, 세번재 말이 10일 때 0101이 주어지게 된다면 3번 말이 두번 우승(01/01) 혹은 1, 2, 3번 말이 한번 우승(0/1/01)으로 해석이 여러개가 될 수 있다. 이러한 경우에 대해서는 decodable하지 않다고 할 수 있다. 즉, 이렇게 code를 부여해서는 안된다. 그래서 위와 같이 0, 10, 110, 1110 등과 같이 code를 부여한 것이다. 이렇게 하면 애매한 해석을 막을 수 있다.

그래서 binary code이기 때문에 base를 2로 하여 entropy를 구하면 $-\sum_{i=1}^8p(i)\;log_2\,p(i)$가 되고 각각의 말에 대해서 code length는 $-log_2\,p(i)$가 된다. 그래서 두번째 말같은 경우에 $p(i)=\frac{1}{4}$가 되어 code가 2 bit가 된 것이다.

Maximizing Information Gain

다시 decision tree로 돌아와서 information gain을 최대로 하는 것은 데이터셋에 대해서 각각의 branch 혹은 spilt을 결정하는 것이다. 우리는 결국에는 surprise를 최소로 하고 싶다. 이것이 decision tree가 좋다고 생각하는 우리의 믿음이다. 좋은 decision tree로부터 우리가 예상하는 것은 surprise와 uncertainty를 최소로 하는 것이고, information gain은 우리가 decision tree를 알고 있다는 사실과 J개의 leaf node를 가지는 decision tree에서 information이 오직 하나의 lable이 되어 surprise나 uncertainty가 없어 최소가 된다는 사실 사이의 difference를 찾으려고 노력한다.

Cutting Down a Complex Model: Neural Network Pruning

지금까지 여러개의 model을 조합하는 방식에 대해서 알아보고 있다. 그러나 요즘 애플 워치, 갤럭시 워치 등 작은 기기는 오랜 시간 사용과 빠른 속도를 위해서 높은 computational efficiency를 요구하고 있다. 그래서 model이 간단하고 parameter 수도 적지만 성능은 완전한 model을 사용했을 때와 마찬가지로 높게 나오기를 원한다. 작지만 효율적인 model을 build하기 위해서 network pruning 기법에 대해서 볼 것이다.

Network Pruning

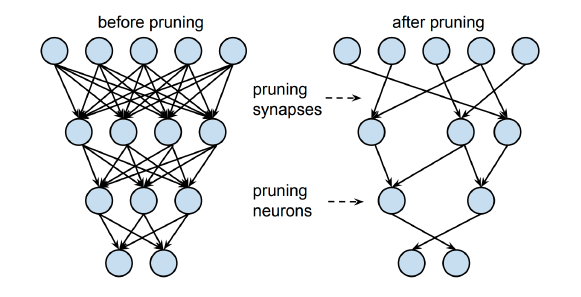
우선은 커다란 neural network model을 알아본 뒤에 불필요한 parameter들을 조금씩 잘라내는 기법을 pruning이라 한다. 한국말로 가지치기를 생각하면 된다. 이 기법을 사용하면 작지만 효율적인 model을 만들 수 있다. Pruning에도 많은 알고리즘들이 존재한다. Pruning은 반복적으로 각각의 layer에서 가장 덜 중요한 neuron을 제거하여 성능을 비교해나간다.

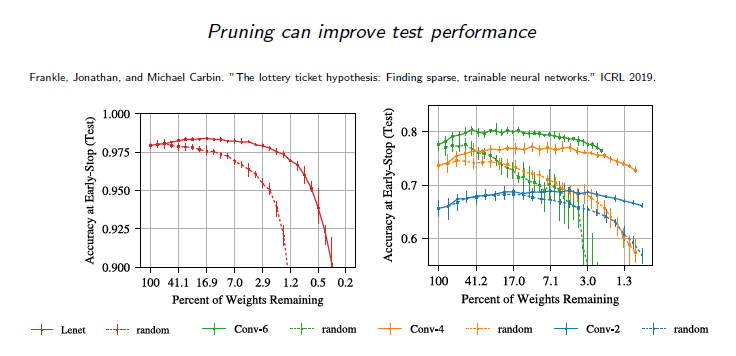
Lottery Ticket Hypothesis

요즘은 무작위로 network를 initialization하는 흥미로운 hypothesis들이 있다. Network의 부분일지라도 처음에 완전한 network를 사용했을 때와 비슷한 성능을 낼 수가 있다.